L'equazione di una circonferenza passante per tre punti non allineati

L'equazione di una circonferenza che passa per tre punti non allineati \( P(x_1, y_1) \), \( Q(x_2, y_2) \) e \( R(x_3, y_3) \) si ottiene risolvendo il seguente sistema di equazioni per i coefficienti "a", "b" e "c". $$ \begin{cases} x_1^2 + y_1^2 + a x_1 + b y_1 + c = 0 \\ x_2^2 + y_2^2 + a x_2 + b y_2 + c = 0 \\ x_3^2 + y_3^2 + a x_3 + b y_3 + c = 0 \end{cases} $$ Una volta trovati i coefficienti "a", "b", "c" vanno sostituiti nell'equazione generale della circonferenza. $$x^2 + y^2 + ax + by + c = 0 $$

Un esempio pratico

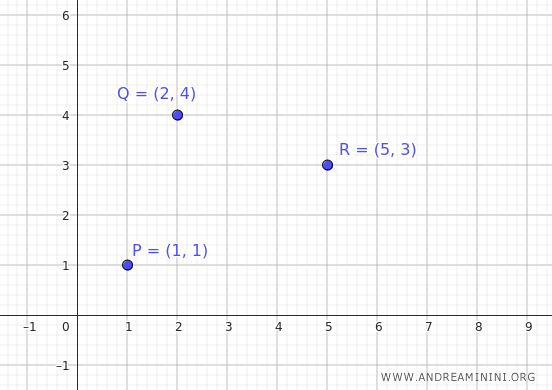
Considero i seguenti punti del piano

$$  P(1, 1) $$

$$  Q(2, 4) $$

$$  R(5, 3) $$

Sono tre punti non allineati del piano cartesiano.

L'equazione generale della circonferenza è:

$$ x^2 + y^2 + ax + by + c = 0 $$

Inserisco le coordinate dei punti nel sistema di equazioni:

• Per il punto P(1,1) sostituisco x=1 e y=1
  $ x^2 + y^2 + ax + by + c = 0 $
  $ 1^2 + 1^2 + a \cdot 1 + b \cdot 1 + c = 0 $
  $ 1 + 1 + a + b + c = 0 $
  $ a + b + c = -2 $
• Per il punto Q(2, 4) sostituisco x=2 e y=4
  $ x^2 + y^2 + ax + by + c = 0 $
  $ 2^2 + 4^2 + a \cdot 2 + b \cdot 4 + c = 0 $
  $ 4 + 16 + 2a + 4b + c = 0 $
  $ 2a + 4b + c = -20 $
• Per il punto R(5, 3) sostituisco x=5 e y=3
  $ x^2 + y^2 + ax + by + c = 0 $
  $ 5^2 + 3^2 + a \cdot 5 + b \cdot 3 + c = 0 $
  $ 25 + 9 + 5a + 3b + c = 0 $
  $ 5a + 3b + c = -34 $

Metto insieme le tre equazioni nel seguente sistema di equazioni lineari:

$$
\begin{cases}
a + b + c = -2 \\
2a + 4b + c = -20 \\
5a + 3b + c = -34 \\
\end{cases} $$

Questo sistema mi permette di trovare i coefficienti "a", "b" e "c" che soddisfano contemporaneamente le tre equazioni delle circonferenze.

A questo punto, devo risolvere il sistema con un metodo di risoluzione qualsiasi.

In questo caso opto per il metodo della riduzione.

Sottraggo la prima equazione dalla seconda:

$$
\begin{cases}
a + b + c = -2 \\
(2a + 4b + c) - (a + b + c) = -20 - (-2) \\
5a + 3b + c = -34 \\
\end{cases} $$

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
5a + 3b + c = -34 \\
\end{cases} $$

Sottraggo la prima equazione dalla terza:

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
(5a + 3b + c) - (a + b + c) = -34 - (-2) \\
\end{cases} $$

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
4a + 2b = -32 \\
\end{cases} $$

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
2a + b = -16 \\
\end{cases} $$

In questo modo elimino la "c" dalle ultime due equazioni e ottengo un sistema più semplice per determinare i valori di "a" e "b".

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
2a + b = -16 \\
\end{cases} $$

Moltiplico la terza equazione per 3:

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
3 \cdot (2a + b) = 3 \cdot ( -16) \\
\end{cases} $$

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
6a + 3b = -48 \\
\end{cases} $$

Ora sottraggo la seconda equazione dalla terza equazione.

In questo modo elimino la variabile "b" e ottengo il valore della variabile "a".

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
6a + 3b - (a+3b) = -48 - (-18)  \\
\end{cases} $$

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
(6a-a) + (3b-3b)= -48 +18   \\
\end{cases} $$

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
5a = -30   \\
\end{cases} $$

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
a = - \frac{30}{5}   \\
\end{cases} $$

$$
\begin{cases}
a + b + c = -2 \\
a + 3b = -18 \\
a = - 6   \\
\end{cases} $$

Una volta trovato il valore della variabile a=-6, lo sostituisco nelle altre equazioni.

$$
\begin{cases}
(-6) + b + c = -2 \\
(-6) + 3b = -18  \\
a = - 6   \\
\end{cases} $$

$$
\begin{cases}
b + c = -2+6 \\
3b = -18 + 6   \\
a = - 6   \\
\end{cases} $$

$$
\begin{cases}
b + c = 4 \\
b = - \frac{12}{3}   \\
a = - 6   \\
\end{cases} $$

$$
\begin{cases}
b + c = 4 \\
b = - 4   \\
a = - 6   \\
\end{cases} $$

Ho trovato anche il valore della variabile b=-4 che sostituisco nella prima equazione.

$$
\begin{cases}
-4 + c = 4 \\
b = - 4   \\
a = - 6   \\
\end{cases} $$

$$
\begin{cases}
c = 4+4 \\
b = - 4   \\
a = - 6   \\
\end{cases} $$

$$
\begin{cases}
c = 8 \\
b = - 4   \\
a = - 6   \\
\end{cases} $$

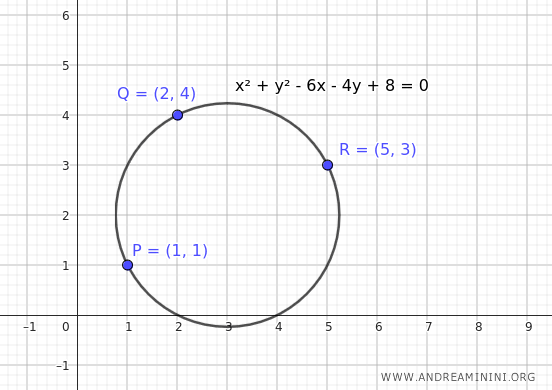
Ho trovato i tre coefficienti a=-6 , b=-4 e c=8.

Pertanto, l'equazione della circonferenza che passa per i tre punti A, B, C è la seguente:

$$ x^2 + y^2 + ax + by + c = 0 $$

$$ x^2 + y^2 - 6x - 4y + 8 = 0 $$

Ecco il grafico della circonferenza:

La dimostrazione

L'equazione della circonferenza è data nella forma

$$x^2 + y^2 + ax + by + c = 0 $$

Per fare in modo che la circonferenza passi per i punti \( P \), \( Q \) e \( R \), le coordinate di ciascun punto devono soddisfare questa equazione.

• Punto P(x₁,y₁) $$ x_1^2 + y_1^2 + a x_1 + b y_1 + c = 0 $$
• Punto Q(x₂,y₂) $$ x_2^2 + y_2^2 + a x_2 + b y_2 + c = 0 $$
• Punto R(x₃,y₃) $$ x_3^2 + y_3^2 + a x_3 + b y_3 + c = 0 $$

I coefficienti "a", "b" e "c" sono gli stessi in tutte le equazioni.

Quindi, posso costruire un sistema di equazioni:

$$
\begin{cases}
x_1^2 + y_1^2 + a x_1 + b y_1 + c = 0 \\
x_2^2 + y_2^2 + a x_2 + b y_2 + c = 0 \\
x_3^2 + y_3^2 + a x_3 + b y_3 + c = 0 \\
\end{cases}
$$

A questo punto, risolvo il sistema di equazioni per trovare i coefficienti \( a \), \( b \) e \( c \), che definiscono la circonferenza che passa per i punti dati.

Una volta ottenuti, li sostituisco nell'equazione generale della circonferenza.

$$x^2 + y^2 + ax + by + c = 0 $$

E così via.