Come ricavare l'equazione della circonferenza noti gli estremi del diametro
Per trovare l'equazione della circonferenza a partire dagli estremi A e B di un diametro posso seguire questa procedura:
- Determino il centro della circonferenza
Il centro \( C \) della circonferenza è il punto medio del segmento che collega i punti \( A \) e \( B \) (gli estremi del diametro). Se \( A \) ha coordinate \((x_A, y_A)\) e \( B \) ha coordinate \((x_B, y_B)\), il centro \( C \) avrà coordinate: $$ \left( \frac{x_A + x_B}{2}, \frac{y_A + y_B}{2} \right) $$ - Calcolo del raggio
Il raggio \( r \) è la metà della distanza tra i punti \( A \) e \( B \). La distanza tra \( A \) e \( B \) può essere calcolata semplicemente usando la formula della distanza euclidea: $$ AB = \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$ Quindi, il raggio \( r \) è: $$ r = \frac{1}{2} \cdot \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$ - Equazione della circonferenza
Una volta determinati il centro \( C(x_0, y_0) \) e il raggio \( r \), posso scrivere l'equazione della circonferenza nella forma standard: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$ dove \( x_0 = \frac{x_A + x_B}{2} \) e \( y_0 = \frac{y_A + y_B}{2} \).
Un esempio pratico
Faccio un esempio pratico per chiarire il procedimento.
Considero due punti \( A(2, 3) \) e \( B(8, 7) \) che rappresentano gli estremi di un diametro di una circonferenza.
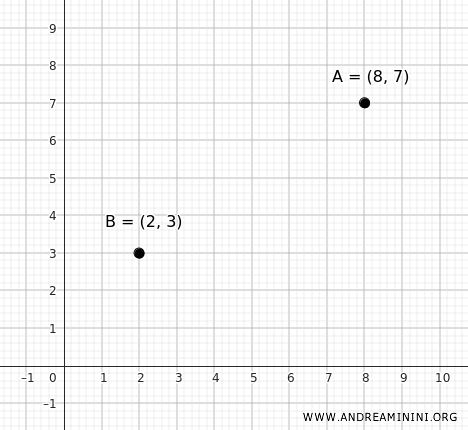
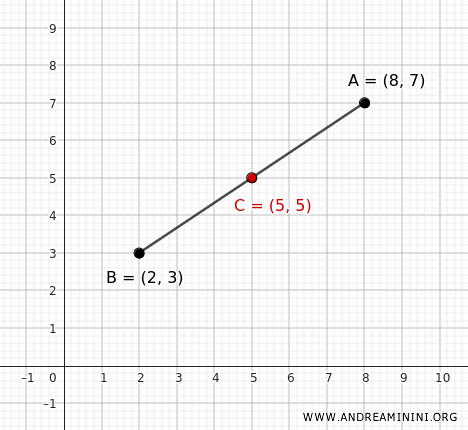
Il centro \( C \) è il punto medio del segmento \( AB \):
$$ C \left( \frac{x_A + x_B}{2}, \frac{y_A + y_B}{2} \right) $$
$$ C \left( \frac{2 + 8}{2}, \frac{3 + 7}{2} \right) $$
$$ C \left( \frac{10}{2}, \frac{10}{2} \right) $$
$$ C(5, 5) $$
Quindi, il centro della circonferenza si trova alle coordinate $ C(5, 5) $ del piano cartesiano.
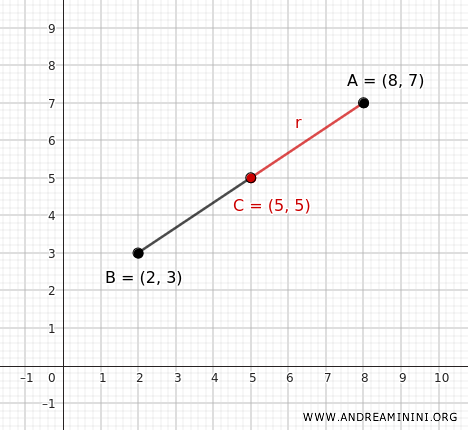
La distanza \( AB \) tra i punti \( A \) e \( B \) si ottiene tramite la formula della distanza euclidea tra due punti del piano:
$$ AB = \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$
$$ AB = \sqrt{(2 - 8)^2 + (3 - 7)^2} $$
$$ AB = \sqrt{(-6)^2 + (-4)^2} $$
$$ AB = \sqrt{36 + 16} $$
$$ AB = \sqrt{52} $$
$$ AB = 2\sqrt{13} $$
Sapendo che il raggio della circonferenza è la metà del diametro, divido a metà la distanza AB tra i punti A e B.
$$ r = \frac{1}{2} \cdot AB $$
$$ r = \frac{1}{2} \cdot 2\sqrt{13} $$
$$ r= \sqrt{13} $$
Quindi, il raggio è $ r= \sqrt{13} $.
A questo punto posso scrivere l'equazione della circonferenza con centro \( C(5, 5) \) e raggio \( r = \sqrt{13} \).
La formula della circonferenza noti il centro e il raggio è la seguente:
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
In questo caso le coordinate del centro sono \( x_0 = 5 \) e \( y_0 = 5 \), quindi l'equazione diventa:
$$ (x - 5)^2 + (y - 5)^2 = (\sqrt{13})^2 $$
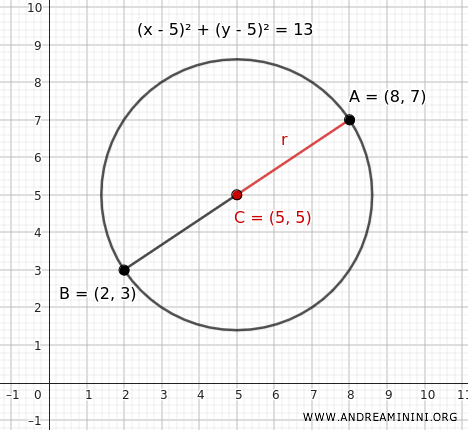
$$ (x - 5)^2 + (y - 5)^2 = 13 $$
Questa è l'equazione della circonferenza che ha come diametro il segmento con estremi \( A(2, 3) \) e \( B(8, 7) \).
E così via.
