La bisettrice in un triangolo isoscele
In un triangolo isoscele la bisettrice dell'angolo opposto alla base coincide con la mediana e l'altezza.
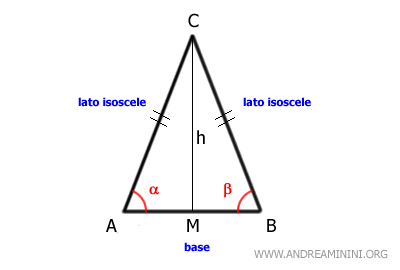
La dimostrazione
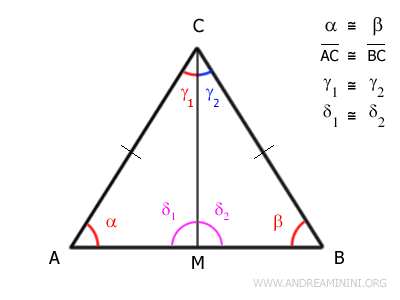
Considero un triangolo isoscele ABC
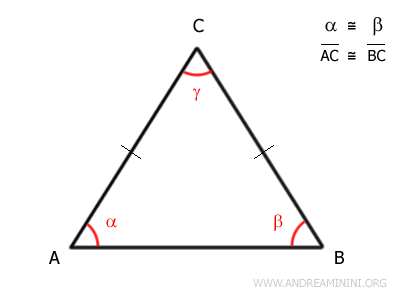
Essendo un triangolo isoscele ha due lati congruenti AC≅BC e gli angoli adiacenti alla base congruenti α≅β.
$$ \overline{AC} = \overline{BC} $$
$$ \alpha = \beta $$
Traccio la bisettrice CM dell'angolo γ al vertice opposto alla base.
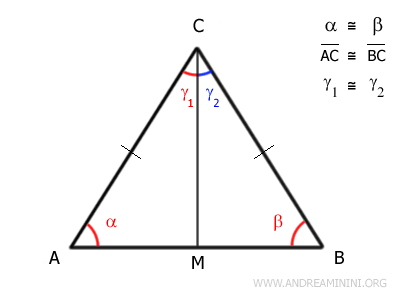
La bisettrice BM divide l'angolo γ a metà. Quindi, ottengo due angoli congruenti γ1≅γ2.
$$ \gamma_1 \cong \gamma_2 $$
La bisettrice divide il triangolo in due triangoli rettangoli ACM e BCM che hanno:
- lo stesso lato CM
- due lati congruenti AC≅BC
- gli angoli tra i lati congruenti γ1≅γ2
Quindi, per il primo principio della congruenza, i triangoli AMC e BMC sono congruenti.
$$ AMC \cong BMC $$
Essendo due triangoli congruenti ACM≅BCM hanno i lati e gli angoli congruenti nello stesso ordine.
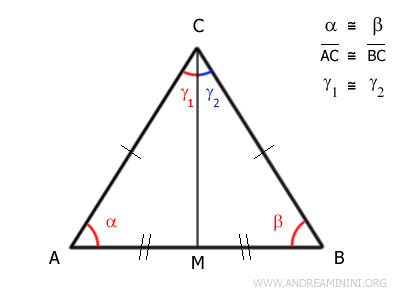
In particolar modo, per la dimostrazione mi interessa che siano congruenti i lati AM e BM.
$$ AM \cong BM $$
Questo vuol dire che i due segmenti AM e BM hanno la stessa lunghezza. Quindi, il punto M è il punto medio del segmento AB.
Pertanto, la bisettrice CM è anche la mediana rispetto alla base AB del triangolo isoscele.
Inoltre, sapendo che ACM≅BCM sono triangoli congruenti anche i loro angoli sono congruenti nello stesso ordine.
In particolar modo, mi è utile sapere che gli angoli δ1≅δ2 sono congruenti.
$$ \delta_1 \cong \delta_2 $$
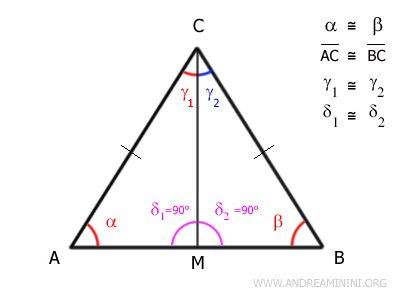
I due angoli δ1≅δ2 sono anche supplementari δ1+δ2 =180° perché la loro somma è uguale a un angolo piatto (180°).
Quindi, se gli angoli sono congruenti e supplementari, questo vuol dire che sono entrambi due angoli retti (90°).
$$ \delta_1 = \delta_2 = 90° $$
Questo dimostra che la bisettrice CM è anche l'altezza del triangolo isoscele.
E così via.
