La retta secante, tangente o esterna a una circonferenza

Data una circonferenza con centro nel punto C e un raggio r, posso capire se una retta t è secante, tangente o esterna analizzando se la distanza tra il punto C e la retta è inferiore, uguale o maggiore al raggio. $$ d(C,retta)<raggio \:\: \rightarrow retta \: secante $$ $$ d(C,retta)=raggio \:\: \rightarrow retta \: tangente $$ $$ d(C,retta)>raggio \:\: \rightarrow retta \: esterna $$ dove la distanza è $$ D(C(x_0,y_0),retta) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$

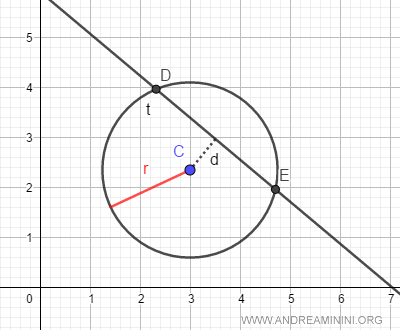
Se la retta è secante, la circonferenza ha due punti in comune con la retta.

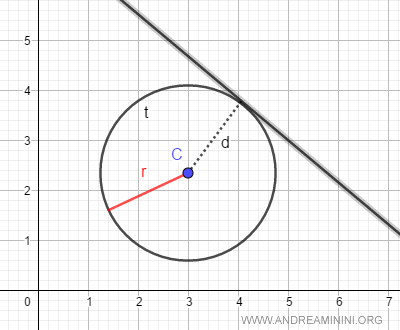
Se la retta è tangente, la circonferenza ha un solo punto in comune con la retta ( punto di tangenza ).

Se la retta è esterna, non ci sono punti in comune con la circonferenza.

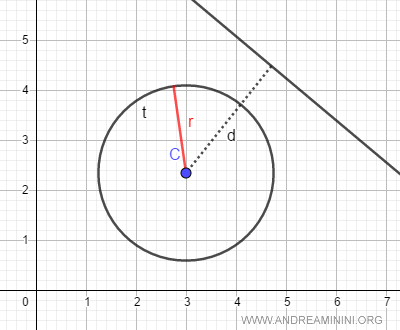
Nota. In questo caso il semento della distanza d ( distanza minima tra la retta e il centro della circonferenza ) è più lungo rispetto al segmento r del raggio.

Esempio

Ho una circonferenza

$$ (x-3)^2+(y-2)^2-3=0 $$

e una retta

$$ 2x-5y-6=0 $$

Devo capire se la retta è secante, tangente o esterna.

Per prima cosa, trasformo l'equazione della circonferenza nella forma canonica (x²+y²)+ax+bx+c.

$$ (x-3)^2+(y-2)^2-3=0 $$

$$ (x^2-6x+9)+(y^2-4y+4)-3=0 $$

$$ (x^2+y^2)-6x-4y+10=0 $$

Poi trovo le coordinate del centro della circonferenza e della lunghezza del raggio tramite le formule della circonferenza.

$$ \begin{cases} x_0 = - \frac{a}{2} \\ y_0 = - \frac{b}{2} \\ r = \sqrt{x_0^2 + y_0^2 - c} \end{cases} $$

Sostituisco i coefficienti a=-6, b=-4 e c=10 dell'equazione della circonferenza.

$$ \begin{cases} x_0 = - \frac{-6}{2} = 3 \\ y_0 = - \frac{-4}{2} =2 \\ r = \sqrt{(3)^2 + (2)^2 - (10)} = \sqrt{9+4-10} = \sqrt{ 3 } \approx 1,73 \end{cases} $$

Quindi, le coordinate del punto C centrale e del raggio r della circonferenza sono:

$$ C = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$

$$ r \approx 1,73 $$

A questo punto, posso calcolare la distanza minima d tra la retta e il punto C del centro della circonferenza.

$$ d(C(x_0,y_0),retta) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$

$$ d(C(x_0,y_0),retta) = \frac{|2x_0-5y_0-6=0|}{\sqrt{2^2+(-5)^2}} $$

dove x₀=3, y₀=2 sono le coordinate del centro della circonferenza

$$ d = \frac{|2 \cdot (3)-5 \cdot (2) -6|}{\sqrt{4+25} } $$

$$ d = \frac{|-10|}{\sqrt{29}} $$

$$ d = \frac{10}{\sqrt{29}} \approx 1,86 $$

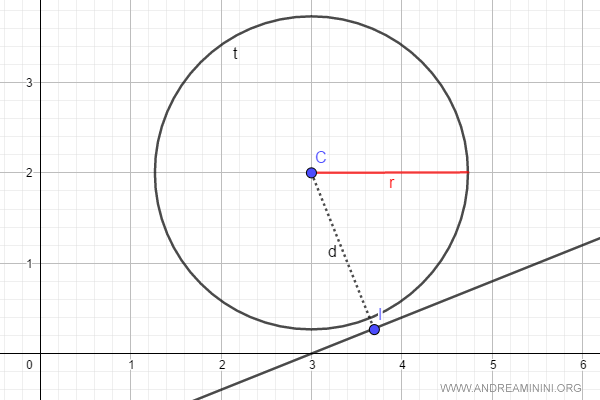
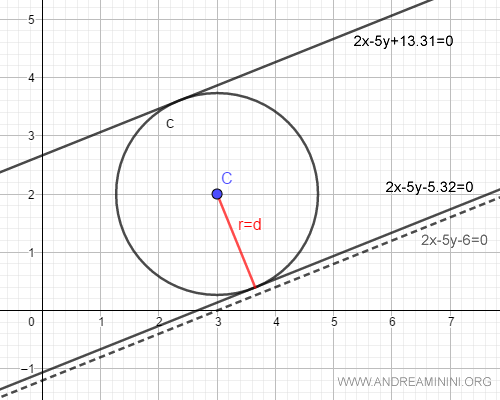
La distanza minima (d) tra il centro C della circonferenza e la retta è approssimativamente 1,86

Si tratta di una retta esterna alla circonferenza perché la distanza ( d=1,86 ) è maggiore del raggio ( r=1,73 ).

$$ d > r $$

Come si può vedere nella rappresentazione grafica

Esempio 2 ( retta tangente )

Ora voglio trovare la retta parallela tangente alla circonferenza.

So già che il parametro che determina il fascio di rette è il coefficiente c della retta.

$$ ax + by + c = 0 $$

Quindi, il coefficiente c è l'incognita del problema.

$$ 2x-5y+c=0 $$

La retta è tangente alla circonferenza se la distanza d(C,retta) è uguale al raggio.

$$ d(C,retta) = r = 1,73 $$

Quindi, riscrivo la formula della distanza senza sostituire il valore del coefficiente c della retta

$$ d(C(x_0,y_0),retta) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} = r $$

$$ d(C(x_0,y_0),retta) = \frac{|2x_0-5y_0+c=0|}{\sqrt{2^2+(-5)^2}} = 1,73 $$

dove x₀=3, y₀=2 sono le coordinate del centro della circonferenza

$$ \frac{|2 \cdot (3)-5 \cdot (2) +c|}{\sqrt{4+25} } = 1,73 $$

$$ \frac{|6-10 +c|}{\sqrt{29} } = 1,73 $$

$$ c = ± 1,73 \cdot \sqrt{29} + 4 $$

$$ \begin{cases} c = + \sqrt{29} \cdot 1,73 + 4 \approx 13,31 \\ c = - \sqrt{29} \cdot 1,73 + 4 \approx -5,31 \end{cases} $$

La retta è tangente alla circonferenza se il parametro c è uguale a 13,31 oppure a -5,31

Nota. I valori precisi del coefficiente c sono i numeri reali 13.3163351163 e -5.31633511634. Per semplicità espositiva li ho approssimati a due posizioni decimali.

Verifica

Calcolo l'equazione della retta tangente con il nuovo coefficiente c

$$ 2x-5y+c=0 $$

E ottengo due equazioni

$$ 2x-5y+31,31=0 $$

$$ 2x-5y-5,31=0 $$

Le due rette appartengono effettivamente al fascio di rette improprio della retta iniziale ( linea tratteggiata ). Sono rette parallele.

Inoltre, sono entrambe rette tangenti alla circonferenza.

E così via.