La circonferenza
Una circonferenza è l'insieme dei punti P del piano che hanno la stessa distanza r ( raggio ) dal punto centrale. $$ d(C,P)=r $$
L'equazione cartesiana della circonferenza
L'equazione cartesiana della circonferenza è la seguente:
$$ x^2+x^2+ax+by+c= 0 $$
purché soddisfi la condizione
$$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$
oppure in forma canonica
$$ \sqrt{(x-x_0)^2+(y-y_0)^2} = r $$
Dove (x0,y0) sono le coordinate del punto centrale della circonferenza.
Le coordinate (x,y) sono le generiche coordinate dei punti della circonferenza.
Dimostrazione:
Per trovare la formula della circonferenza, basta ricordarsi quella della distanza.
Dati due punti
$$ P \begin{pmatrix} x \\ y \end{pmatrix} $$
$$ C \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} $$
La distanza tra i due punti è la seguente
$$ \sqrt{(x-x_0)^2+(y-y_0)^2} $$
L'insieme dei punti P con eguale distanza (r) dal punto C è determinato da
$$ \sqrt{(x-x_0)^2+(y-y_0)^2} = r $$
Quest'ultima è detta equazione cartesiana della circonferenza in forma canonica.
L'equazione equivale a
$$ (x-x_0)^2+(y-y_0)^2 = r^2 $$
$$ x^2-2xx_0+x_0^2+y^2-2yy_0+y^2 - r^2 = 0 $$
Raggruppando alcuni termini ottengo l'equazione cartesiana della circonferenza
$$ x^2+x^2+ax+by+c= 0 $$
Dove
$$ a = -2x_0 $$
$$ b = -2y_0 $$
$$ c = x_0^2 + y_0^2 -r^2 $$
che equivale a dire
$$ x_0 = - \frac{a}{2} $$
$$ y_0 = - \frac{b}{2} $$
$$ r = \sqrt{x_0^2 + y_0^2 - c} $$
Esempi
Esempio 1
Data un'equazione
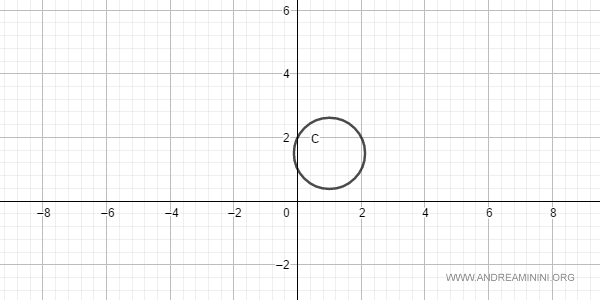
$$ x^2+y^2-2x-3y+2=0 $$
I coefficienti sono
$$ a=-2 $$
$$ b=-3 $$
$$ c=+2 $$
Per sapere se l'equazione è una circonferenza, devo verificare se soddisfa la condizione.
$$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$
$$ \frac{(-2)^2}{4} + \frac{(-3)^2}{4} - 2 \ge 0 $$
$$ 1 + \frac{9}{4} - 2 \ge 0 $$
$$ \frac{5}{4} \ge 0 $$
La disequazione è soddisfatta, si tratta di una circonferenza.
Esempio 2
Data la seguente equazione di 2° grado
$$ \frac{x^2}{2}+\frac{y^2}{2}-3x+5y-2=0 $$
In questo caso devo prima trasformare i coefficienti di x2 e y2 in coefficienti unitari, moltiplicando tutta l'equazione per 2.
$$ 2 \cdot ( \frac{x^2}{2}+\frac{y^2}{2}-3x+5y-2 ) =0 $$
Ottengo così la forma normalizzata dell'equazione della circonferenza
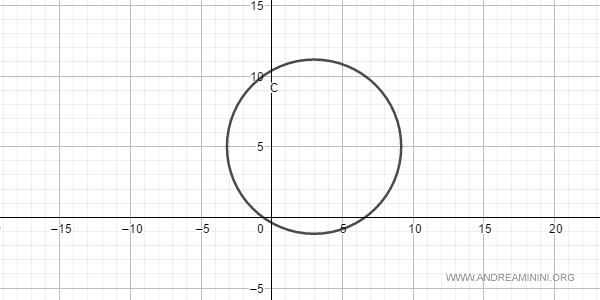
$$ x^2+y^2-6x+10y-4=0 $$
In questa forma posso verificare se soddisfa la condizione delle circonferenze oppure no.
Attenzione. Se un'equazione polinomiale di 2° non è riconducibile alla forma x2 + y2, se i coefficienti sono diversi, allora non è una circonferenza. Sarebbe del tutto inutile verificare i coefficienti nella formula della circonferenza.
I coefficienti dell'equazione normalizzata sono
$$ a=-3 $$
$$ b=10 $$
$$ c=-4 $$
A questo punto li sostituisco nella formula della circonferenza
$$ \frac{(-3)^2}{4} + \frac{(10)^2}{4} - (-4) \ge 0 $$
$$ \frac{9}{4} + \frac{100}{4} +4 \ge 0 $$
$$ \frac{9+100+16}{4} \ge 0 $$
$$ \frac{125}{4} \ge 0 $$
La disequazione è soddisfatta.
Si tratta di una circonferenza.
Esempio 3
Ho la seguente equazione
$$ x^2+y^2-2x+5y+8=0 $$
I coefficienti sono
$$ a=-2 $$
$$ b=5 $$
$$ c=8 $$
Verifico se è una circonferenza
$$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$
$$ \frac{(-2)^2}{4} + \frac{5^2}{4} - 8 \ge 0 $$
$$ \frac{4+25-32}{4} \ge 0 $$
$$ \frac{-3}{4} \ge 0 $$
La condizione non è soddisfatta.
Pertanto, l'equazione non è una circonferenza.
E così via.
