Fasci di rette
Cos'è un fascio di rette
Un fascio di rette è un insieme di rette del piano individuate tramite un determinato criterio di selezione.
Esistono due tipi di fasci di rette: propri e impropri
Fascio improprio di rette
Un fascio improrio di rette è l'insieme di tutte le rette parallele a una determinata retta r del piano.
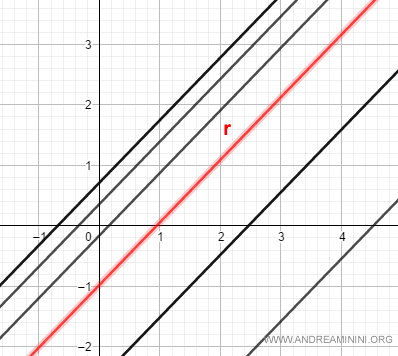
L'equazione cartesiana del fascio improprio di rette è
$$ ax + by + c = 0 $$
Dove i coefficienti a e b sono non nulli.
Ogni retta è individuata da un determinato valore di c.
Nota. Anche la retta r, quella a cui sono parallele tutte le altre, è caratterizzata da un determinato valore di c.
In alternativa, posso scrivere l'equazione del fascio improprio di rette in forma esplicita
$$ y = mx + q $$
In questo caso ogni retta è caratterizzata da un valore diverso del termine q.
Per q=0 la retta passa per l'origine.
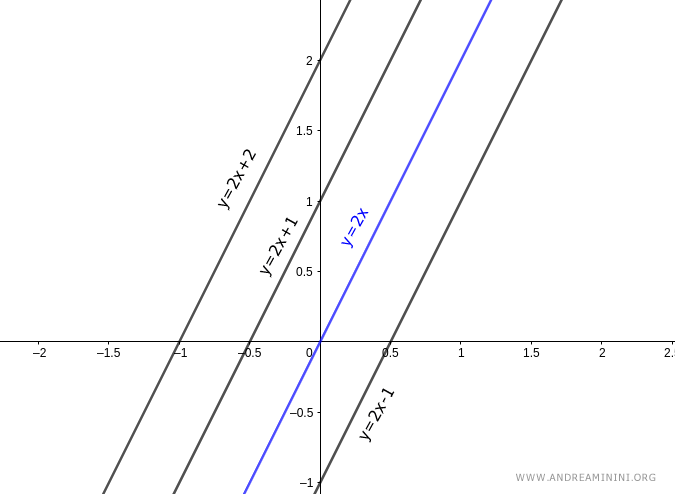
Nota. Il termine q indica l'intercetta sull'asse delle ordinate, ossia il punto in cui la retta interseca l'asse y quando x=0.
L'equazione parametrica del fascio di rette è
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$
In questo caso ogni retta del fascio improprio è individuata al variare della combinazione (x0,y0).
Il vettore direttore ( l,m) è invece sempre lo stesso in ogni retta parallela.
Esempio
L'equazione cartesiana di una retta è
$$ 2x +3y - 12 = 0 $$
Modificando il parametro c=12 con altri valori ottengo le infinite rette parallele del fascio improprio.
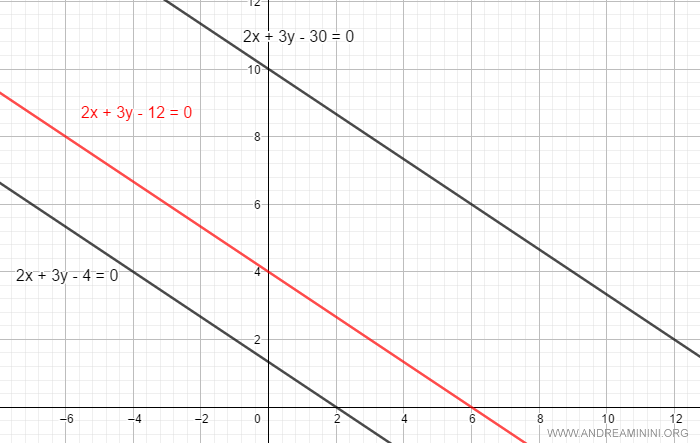
Posso scrivere il fascio di rette anche come equazione parametrica.
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ -\frac{2}{3} \end{pmatrix} $$
Modificando il parametro (0,4) dell'intercetta ottengo tutte le altre rette, lasciando invariato il vettore direttore.
Il risultato è sempre lo stesso.
Fascio proprio di rette
Un fascio proprio di rette è l'insieme di tutte le rette che passano per un particolare punto (A) del piano detto centro di fascio.
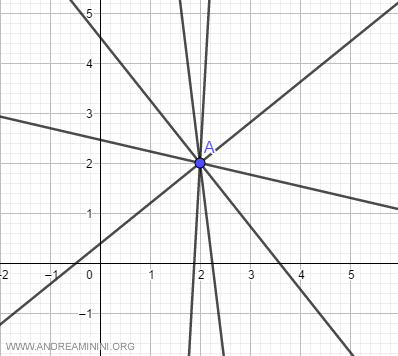
L'equazione del fascio proprio di rette con centro un punto di coordinate (x0,y0) è
$$ y-y_0 = m \cdot (x-x_0) $$
Al variare del coefficiente angolare m∈R ottengo tutte le rette del fascio di rette proprio passanti per il punto A tranne la retta parallela all'asse y.
Nota. La retta parallela all'asse y non è esprimibile con l'equazione della retta in forma esplicita y=mx perché non esiste alcun valore m che ne fornisca l'equazione. Nel caso delle rette parallele all'asse y si utilizza l'equazione x=x0. $$ x = x_0 $$
Pertanto il fascio completo di rette è descritto con le equazioni
$$ \begin{cases} y-y_0 = m \cdot (x-x_0) \\ \\ x=x_0 \ \ \ \text{se la retta è parallela all'asse y} \end{cases} $$
Esempio
Considero un centro di fascio C
$$ C = \begin{pmatrix} x_0 = 2 \\ y_0 = 3 \end{pmatrix} $$
Le equazioni del centro di fascio sono rappresentabili con queste due equazioni
$$ y-y_0 = m \cdot (x-x_0) $$
$$ x = x_0 $$
Sapendo che x0=2 e y0=3 le equazioni del fascio di rette diventano
$$ y-3 = m \cdot (x-2) $$
$$ x = 2 $$
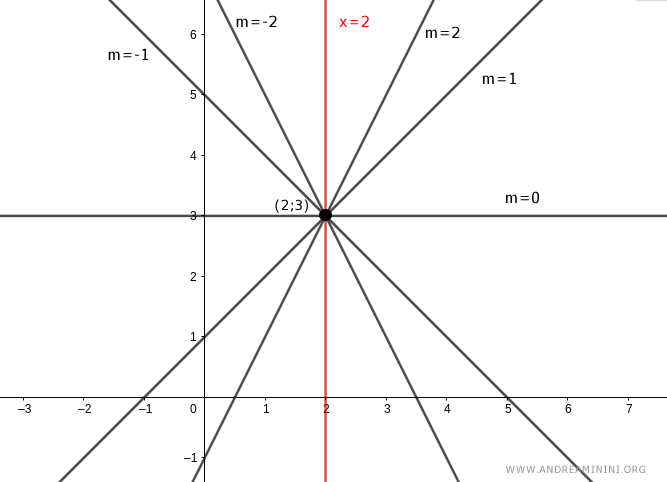
La prima equazione y-3=m(x-2) rappresenta tutte le rette al variare del coefficiente angolare m tranne la retta parallela all'asse y.
La seconda equazione x=2 rappresenta la retta parallela all'asse y (retta di colore rosso).
Il fascio di rette come combinazione lineare di due rette
Un fascio di rette proprio o improprio posso generarlo anche utilizzando una combinazione lineare di due rette.
$$ r: ax+by+c=0 $$
$$ s: a'x+b'y+c'=0 $$
La combinazione lineare delle due rette è la seguente:
$$ p \cdot (ax+by+c) + q \cdot ( a'x+b'y+c' ) = 0 $$
Divido entrambi i lati dell'equazione per p e ottengo
$$ ax+by+c + \frac{q}{p} \cdot ( a'x+b'y+c' ) = 0 $$
Ora assegno $ k = \frac{q}{p} $
$$ ax+by+c + k \cdot ( a'x+b'y+c' ) = 0 $$
$$ ax+by+c + a'xk+b'yk+c'k = 0 $$
A ogni valore di $ k $ corrisponde una e una sola retta del fascio di retta.
Nota. Questa combinazione lineare rappresenta tutte le rette del fascio tranne la retta $ s: a'x+b'y+c'=0 $ perché nessun valore $ k $ corrisponde alla retta $ s $. $$ ax+by+c + k \cdot ( a'x+b'y+c' ) = 0 $$
Metto in evidenza i fattori in comune x e y
$$ (ax+a'xk)+(by+b'yk)+c+c'k = 0 $$
$$ (a+a'k) \cdot x+(b+b'k) \cdot y +c+c'k = 0 $$
Quest'ultima è l'equazione generale del fascio di rette.
Il fascio di rette può essere proprio o improprio
- Fascio di rete proprio
Si ottiene se il rapporto tra i coefficienti a e b delle equazioni è diverso $$ \frac{a}{b} \ne \frac{a'}{b'} $$ - Fascio di rete improprio
Si ottiene se il rapporto tra i coefficienti a e b delle equazioni è uguale perché le due rette sono parallele o coincidenti. $$ \frac{a}{b} = \frac{a'}{b'} $$
Esempio
Considero le rette
$$ r: 3x+6y+4=0 $$
$$ s: 6x-4y-1=0 $$
Ecco la rappresentazione delle due rette nel piano.
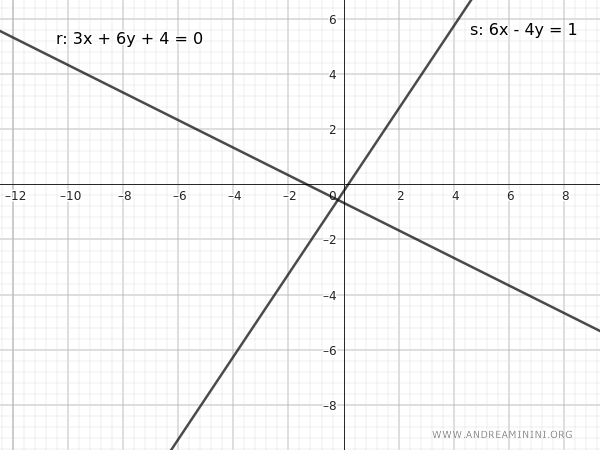
In questo caso sono due rette incidenti perché il rapporto tra i coefficienti è diverso
$$ \frac{a}{b} \ne \frac{a'}{b'} $$
$$ \frac{3}{6} \ne \frac{6}{4} $$
Quindi, il fascio di rette sarà un fascio di rette proprio.
La combinazione delle due rette è la seguente:
$$ 3x+6y+4 + k \cdot ( 6x-4y-1 ) = 0 $$
$$ 3x+6y+4 + 6xk-4yk-k = 0 $$
$$ (3x+6xk)+(6y-4yk)+4-k = 0 $$
$$ (3+6k) \cdot x + (6-4k) \cdot y +4-k = 0 $$
Al variare di k posso generare le altre rette del fascio ad eccezione della retta s.
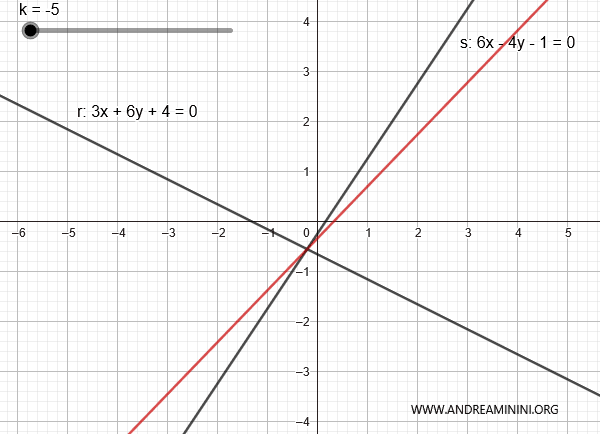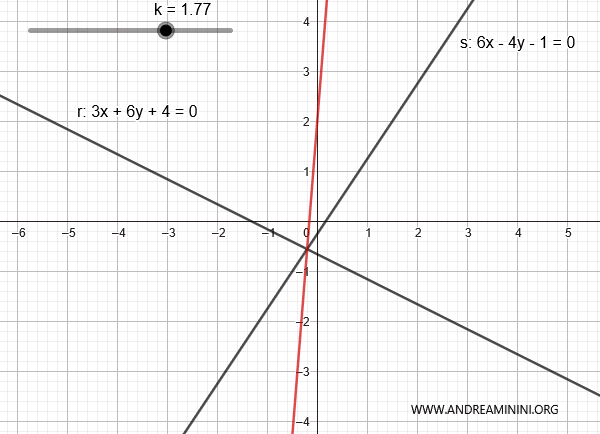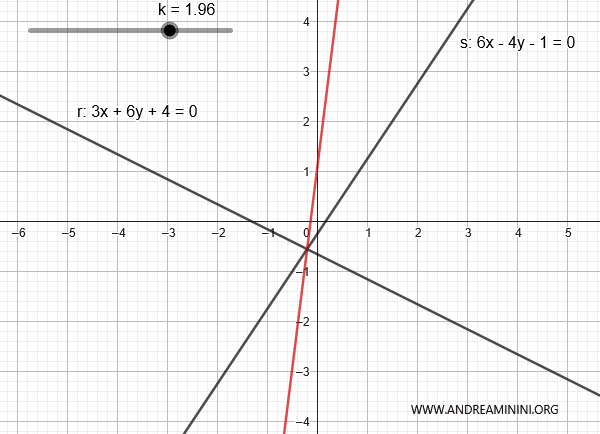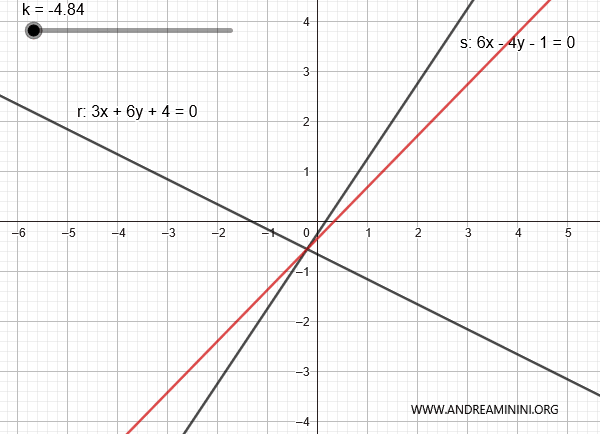
E così via.
