Le rette perpendicolari

Due rette incidenti sono dette rette perpendicolari quando dividono il piano in quattro angoli retti (90°).

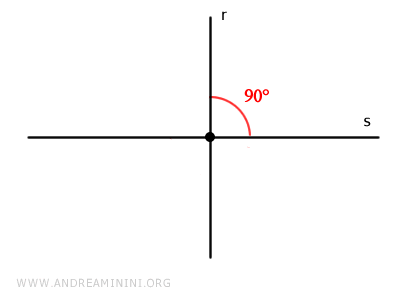
Per indicare due rette perpendicolari si utilizza il simbolo di una T rovesciata. $$ r \perp s $$

Considero due rette distinte r e s sul piano.

Le rette sono rette incidenti perché si intersecano in un solo punto P detto "piede della perpendicolare".

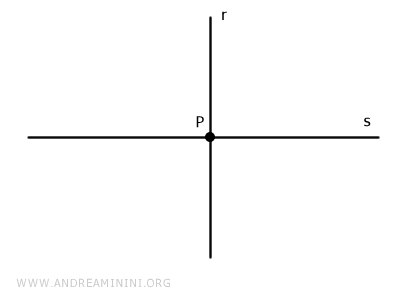
L'intersezione delle due rette divide il piano cartesiano in quattro parti e quattro angoli.

Se un angolo è un angolo retto (90°) lo sono anche tutti gli altri.

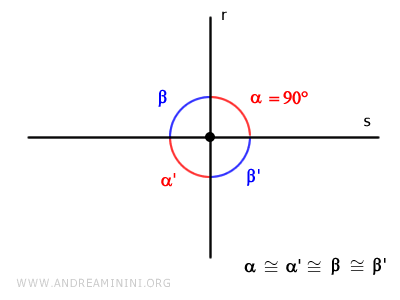
In questo caso le due rette sono tra loro perpendicolari.

Spiegazione. Nel caso di due rette incidenti gli angoli opposti al vertice sono congruenti α≅α' e β ≅β'. $$ \alpha \cong \alpha ' $$ $$ \beta \cong \beta ' $$ Quindi, se un angolo è retto α=90° lo è anche l'angolo α'=90° perché, essendo opposti al vertice, sono tra loro congruenti α≅α' $$ \alpha = \alpha ' = 90° $$ La loro somma è α+α'= 180°. $$ \alpha + \alpha' = 90° + 90° = 180° $$ Sapendo che la somma degli angoli è pari a un angolo giro (360°), anche la somma degli angoli restanti β+β' deve essere pari a 180° $$ \alpha + \alpha ' + \beta + \beta ' = 360° $$ $$ \beta + \beta ' = 360° - ( \alpha + \alpha' ) = 360° - 180° = 180° $$ Gli angoli β e β' sono tra loro congruenti (β≅β') perché sono opposti al vertice. Pertanto, hanno un'ampiezza di 90°. $$ \beta = \beta ' = \frac{180°}{2} = 90° $$ Quindi, tutti gli angoli sono congruenti e l'ampiezza di ciascun angolo è pari a 360°/4 = 90°.

Data una retta r e un punto P che non appartiene alla retta, per il punto P del piano passa una sola retta perpendicolare alla retta r.

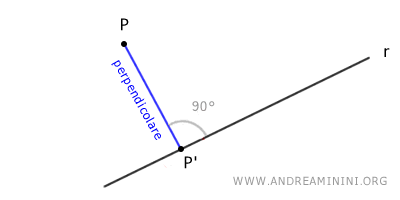
Una retta incidente a un'altra retta senza essere perpendicolare è detta "retta obliqua".

Come verificare se due rette sono perpendicolari?

Nella geometria analitica due rette $ y=mx+q $ e $ y=m'x+q' $ sono perpendicolari se il prodotto dei loro coefficienti angolari è uguale a -1

$$ m \cdot m' = -1 $$

In alternativa, se le equazioni sono in forma implicita, due rette $ ax+by+c=0 $ e $ a'x+b'y+c'=0 $ sono perpendicolari se soddisfano la condizione di perpendicolarità:

$$ aa'+ bb' = 0 $$

Quest'ultima condizione posso applicarla anche se le rette sono parallele agli assi cartesiani.

In ogni caso entrambe le condizioni sono valide per verificare la perpendicolarità delle rette e possono essere utilizzate a seconda della forma delle equazioni. $$ r \perp s \ \Longleftrightarrow \ m \cdot m' = -1 \  \Longleftrightarrow \ aa'+bb'= 0 $$

I coefficienti angolari delle rette perpendicolari

Due rette sono perpendicolari se e solo se il prodotto dei loro coefficienti angolari m e m' è uguale a -1 $$ m \cdot m' = -1 $$ ovvero $$ m = - \frac{1}{m'} $$

Due rette y=mx+q e y+m'x+q' sono rette perpendicolari se si intersecano in un punto formando un angolo di 90°

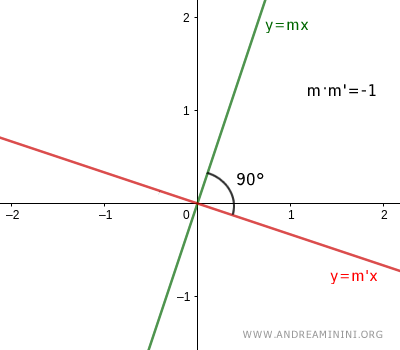
Quando due rette sono perpendicolari il prodotto dei loro coefficienti angolari è uguale a -1.

$$ m \cdot m' = -1 $$

Pertanto, i coefficienti angolari di due rette perpendicolari sono l'uno l'antireciproco (opposto del reciproco) dell'altro

$$ m = - \frac{1}{m'} $$

Questo teorema è applicabile solo se entrambe le rette non sono parallele agli assi.

Nota. Se una delle rette fosse parallela all'asse x avrebbe il coefficiente angolare nullo m=0 e l'antireciproco -1/m sarebbe una divisione per zero. Se una delle due rette fosse parallela all'asse y non potrei calcolare il suo coefficiente angolare con la formula m=y/x. Pertanto, in entrambi i casi il teorema non è applicabile.

Vale anche il ragionamento inverso.

Due rette con il coefficiente m·m'=-1 sono rette perpendicolari.

Un esempio pratico

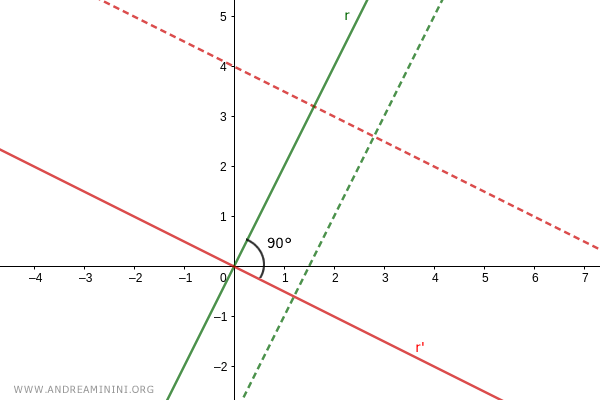
Considero due rette perpendicolari

$$ r = 2x $$

$$ r'= -\frac{1}{2} x $$

Le due rette si intersecano nell'origine formando un angolo di 90°.

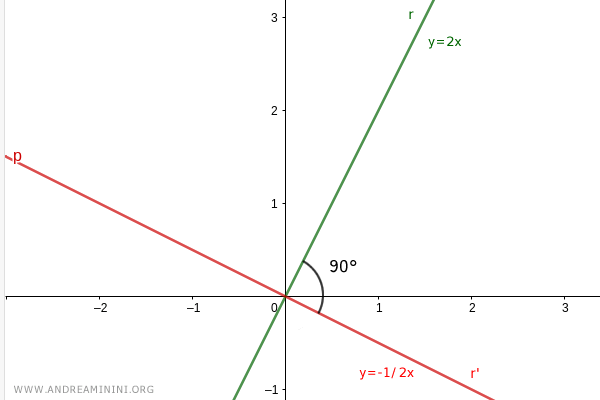
I coefficienti angolari delle due rette sono l'uno l'opposto del reciproco dell'altro.

$$ m=2 $$

$$ m' = - \frac{1}{2} $$

Esempio 2

Considero due rette con i coefficienti angolari antireciproci.

$$ r = 3x $$

$$ r'= -\frac{1}{3} x $$

Traccio le rette sul piano.

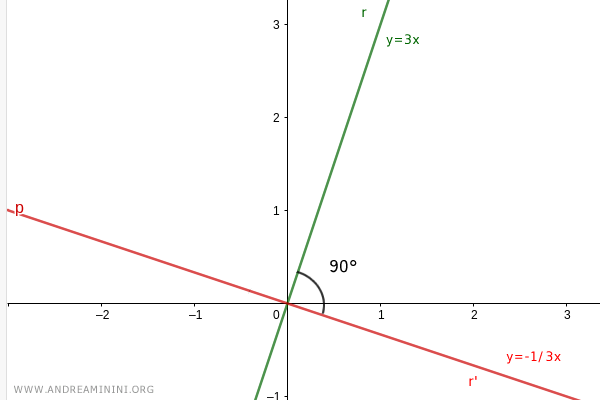
L'angolo tra le due rette è un angolo retto.

Pertanto, le due rette sono perpendicolari.

La dimostrazione

Considero due rette perpendicolari tra loro r e r' non parallele agli assi cartesiani.

$$ r: \ y=mx+q $$ $$ r': \ y=m'x+q' $$

Essendo perpendicolari le due rette si intersecano in un punto formando quattro angoli di 90°

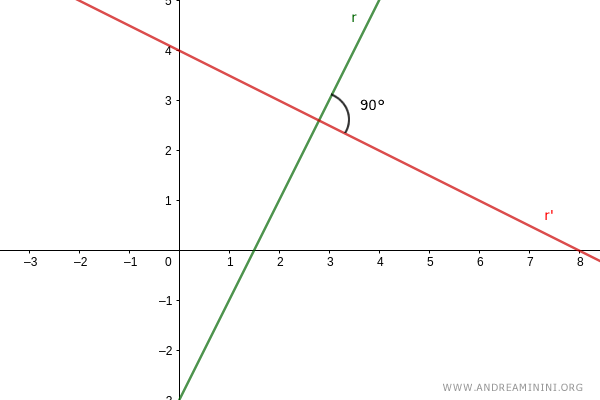
Per semplificare i calcoli considero le rette parallele a r e r' che passano per l'origine (q=0 e q'=0).

Essendo parallele, hanno lo stesso coefficiente angolare m e m' delle precedenti.

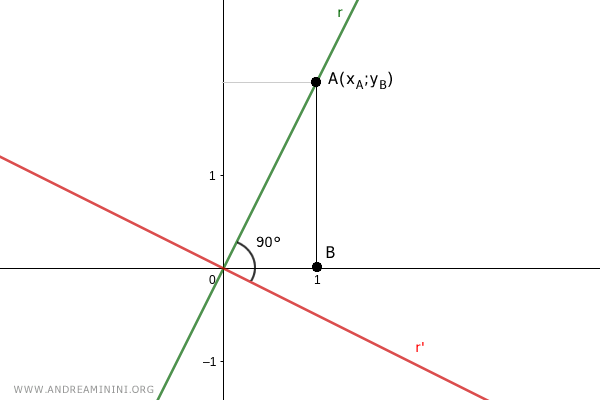
Considero un punto A=(x_A;y_A) sulla retta r con x_A=1.

La sua proiezione sull'asse x è un segmento di lunghezza AB

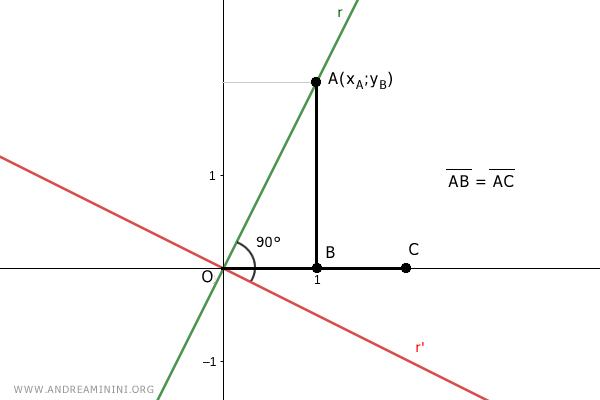
Considero un punto C sull'asse x che dista dall'origine la stessa lunghezza OC=AB

.

Traccio la perpendicolare del punto C fino a intersecare il punto D=(x_D;y_D) sulla retta r'

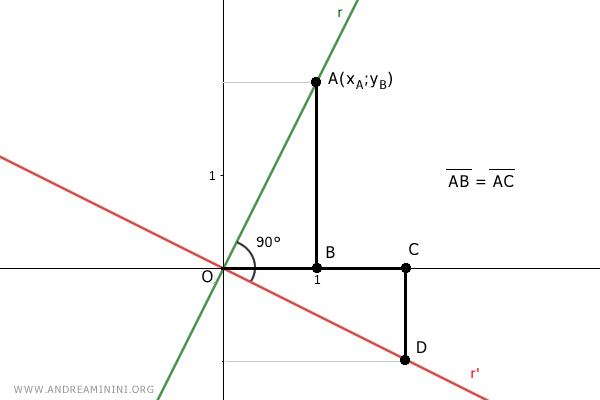
I due triangoli rettangolo OAB e OCD hanno un lato uguale AB=OC perché li ho costruiti in questo modo.

Essendo due triangoli rettangolo hanno entrambi un angolo retto.

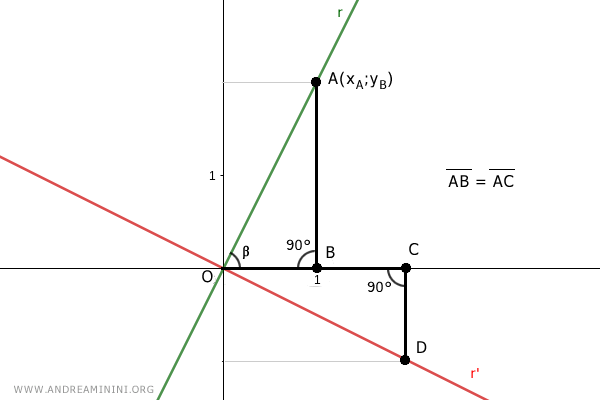
Inoltre, i due triangoli hanno due angoli α e α' complementari dell'angolo β.

Quindi, anche α=α' hanno la stessa ampiezza.

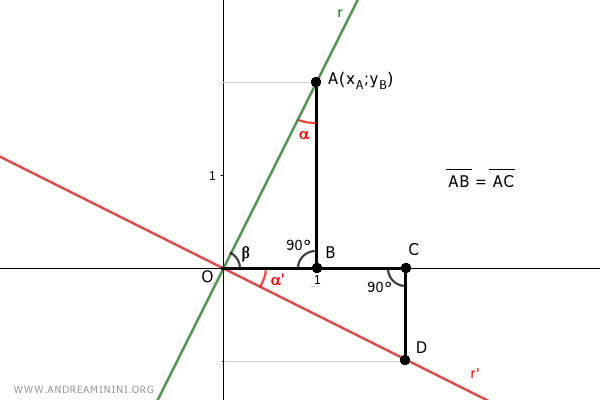
Essendo due triangoli rettangolo la somma degli angoli è 180. Pertanto, anche il terzo angolo dei due triangoli è uguale.

I due triangoli OAB e OCD sono congruenti perché hanno gli angoli congruenti e un lato congruente AB≅OC.

Pertanto, i due triangoli hanno gli stessi lati. In particolar modo, è utile sapere che OA=OC

$$ \overline{OA} = {CD} $$

Sapendo che OA=1 per costruzione anche CD=1

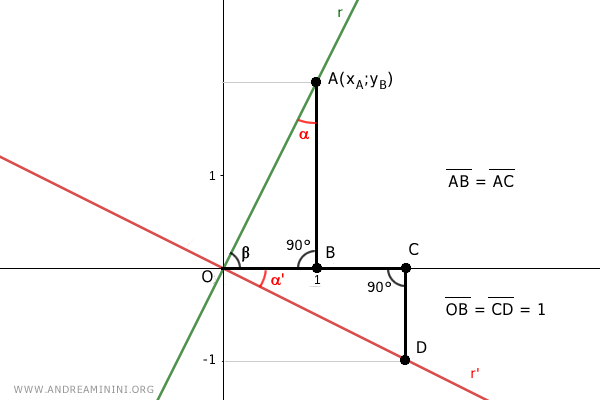
Se il segmento CD=1 allora il punto D si trova alle coordinate D(x_D,-1)

Quindi le coordinate dei punti A e D sono

$$ A=(1;y_A) $$

$$ D=(x_D;-1) $$

Utilizzo le coordinate dei due punti (x_A;y_A)=(1;y_A) e (x_D;y_D)=(x_D;-1) per calcolare i coefficienti angolari delle due rette r e r'

$$ m = \frac{y_A}{x_A} = \frac{y_A}{1} = y_A $$

$$ m' = \frac{y_D}{x_D} = \frac{-1}{x_D} $$

Sapendo che AB=OC per l'ipotesi iniziale allora y_A=x_D

Pertanto, i due coefficienti sono l'uno l'opposto del reciproco dell'altro (antireciproco).

$$ m = y_A $$

$$ m' = - \frac{1}{y_A} $$

Dimostrazione alternativa

Per ipotesi iniziale considero due rette r e r' perpendicolari passanti per l'origine del piano O.

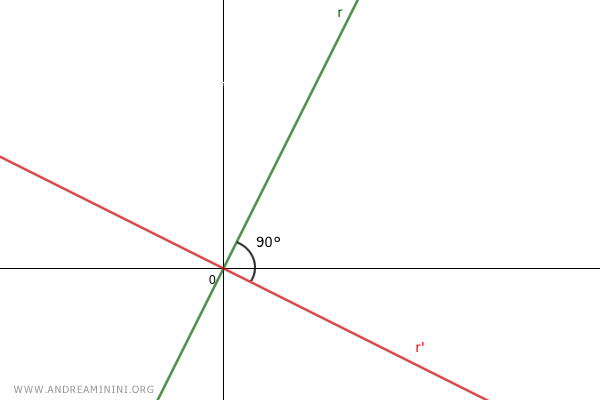
Traccio un segmento unitario OH=1 sull'asse x positivo.

Poi disegno una retta perpendicolare all'asse x che passa per il punto H alle coordinate (1;0) del piano.

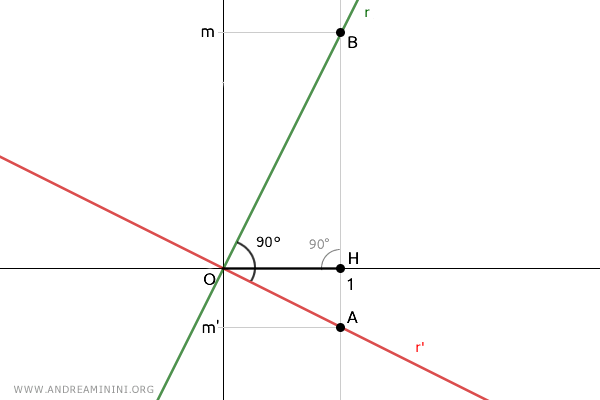
In questo modo individuo i coefficienti angolari delle due rette

$$ m = \frac{ \overline{BH}}{ \overline{OH}} $$

$$ m' = \frac{ \overline{AH}}{ \overline{OH}} $$

Sapendo che OH=1 per costruzione

$$ m = \frac{ \overline{BH}}{ \overline{OH}} = \frac{ \overline{BH}}{1} =  \overline{BH} $$

$$ m' = \frac{ \overline{AH}}{ \overline{OH}} = \frac{ \overline{AH}}{1} =  \overline{AH} $$

Quindi, i coefficienti angolari m e m' sono pari alle lunghezze dei segmenti $ \overline{BH} $ e $ \overline{AH} $.

 

Il triangolo OAB è un triangolo rettangolo perché OA e OB si trovano rispettivamente sulle rette r' e r che per ipotesi iniziale sono perpendicolari tra loro, quindi formano un angolo di 90°.

Inoltre, il segmento OH è l'altezza del triangolo OAB per costruzione, poiché è perpendicolare al lato AB del triangolo.

In base al secondo teorema di Euclide il quadrato dell'altezza relativa all'ipotenusa $ \overline{OH}^2 $ è uguale al prodotto delle proiezioni dei cateti sull'ipotenusa $ \overline{AH} \cdot \overline{BH} $.

$$ \overline(OH)^2 = \overline{AH} \cdot \overline{BH} $$

Sapendo che OH=1.

$$ 1^2 = \overline{AH} \cdot \overline{BH} $$

$$ 1 = \overline{AH} \cdot \overline{BH} $$

Inoltre, sapendo che AH=|m| e BH=|m'|.

$$ 1 = | m | \cdot |m'| $$

Quindi, il prodotto del valore assoluto dei coefficienti angolari m e m' è uguale a 1.

Poiché le rette sono perpendicolari tra loro, il loro prodotto dei coefficienti angolari è negativo.

Del resto si vede già dal grafico che m e m' hanno un segno diverso, ovvero sono numeri discordi.

In questo caso m si trova sul semiasse positivo delle ordinate e quindi e positivo (m>0) mentre m' si trova sul semiasse negativo delle ordinate (m<0).

Pertanto, tolgo il modulo da m e m' deducendo che il prodotto dei coefficienti angolari è uguale a -1.

$$ -1 = m \cdot m' $$

E con questo si conclude la dimostrazione.

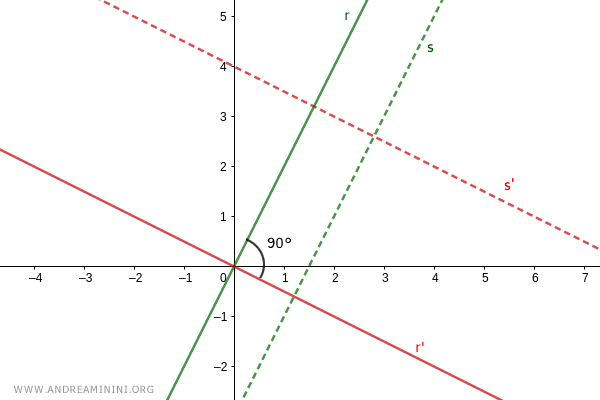
Nota. Questa dimostrazione vale anche se le rette perpendicolari s e s' non passano per l'origine $$ s: \ y = mx+q $$ $$ s': \ y = m'x+q' $$ perché basta individuare le loro rette parallele s||r e s'||r' che passano per l'origine degli assi O(0;0).  $$ r: \ y = mx $$ $$ r': \ y = m'x $$  Se s e s' sono perpendicolari, allora sono perpendicolari anche le loro rette parallele r e r'.

Dimostrazione inversa

In questo caso l'ipotesi iniziale è che due rette hanno il prodotto dei loro coefficienti angolari uguali a -1.

$$ m \cdot m' = -1 $$

Traccio un segmento OH=1 e costruisco il triangolo OAB.

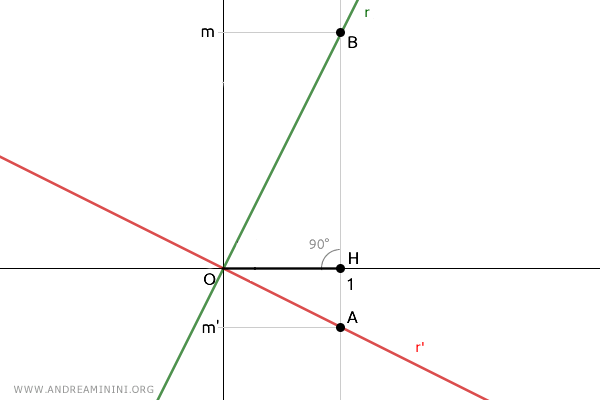
Per dimostrare che le rette r e r' sono rette perpendicolari applico l'inverso del secondo teorema di Euclide. 

Se in un triangolo il quadrato dell'altezza è uguale al prodotto delle lunghezze dei due segmenti in cui il lato opposto è diviso dall'altezza, allora il triangolo è rettangolo e il vertice (C) da cui ha origine l'altezza è un angolo retto (90°).

$$ \overline{OH}^2 = \overline{AH} \cdot \overline{BH} $$

In questo caso AH=|m'| e BH=|m| dove i coefficienti angolari sono sotto modulo perché sto misurando le lunghezze dei segmenti AH e BH.

$$ \overline{OH}^2 = |m'| \cdot |m| $$

Sapendo che $ m \cdot m' = -1 $ per l'ipotesi iniziale, allora $ m'= - \frac{1}{m} $

$$ \overline{OH}^2| = |- \frac{1}{m}| \cdot |m| $$

$$ \overline{OH}^2| = 1 $$

Poiché OH=1 per costruzione l'equazione è soddisfatta.

Pertanto, in base all'inverso del secondo teorema di Euclide l'angolo da cui ha origine l'altezza OH è un angolo retto (90°) e il triangolo OAB è un triangolo retto.

Se OA e OB sono due segmenti perpendicolari tra loro (90°), allora sono perpendicolari anche le rette r' e r in cui si trovano.

Questo dimostra che le due rette r e r' sono perpendicolari tra loro.

La condizione di perpendicolarità

Due rette $ ax+by+c=0 $ e $ a'x+b'y+c'=0 $ sono perpendicolari se soddisfano la condizione di perpendicolarità $$ aa' + bb' = 0 $$

Uno dei vantaggi di questa condizione è che posso utilizzarla per verificare la perpendicolarità anche quando le rette sono parallele agli assi cartesiani.

Esempio

Considero due rette con le equazioni in forma implicita.

$$ r: 2x+4y-6=0 $$

$$ r': 6x-3y-8=0 $$

Per verificare se sono perpendicolari, utilizzo la condizione di perpendicolarità:

$$ aa'+bb'=0 $$

In questo caso, i coefficienti della prima retta sono a=2, b=4 mentre quelli della seconda retta sono a'=6 e b'=-3.

$$ 2 \cdot 6 + 4 \cdot (-3)=0 $$

$$ 12 -12 =0 $$

$$ 0 =0 $$

La condizione è soddisfatta, quindi le due rette r e r' sono perpendicolari.

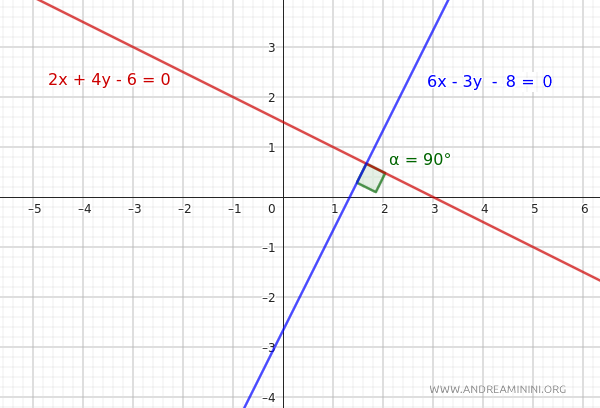
Nota. Per capire a colpo d'occhio se due rette sono perpendicolari, senza guardare il grafico, scrivo le loro equazioni in forma implicita una sotto l'altra, mettendo le variabili x e y in colonna, e calcolo a mente la somma algebrica dei prodotti delle due colonne A e B. Se il risultato è zero, le rette sono perpendicolari.

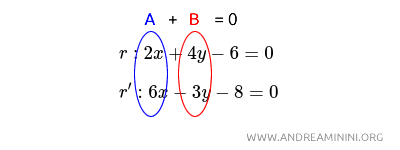
Ad esempio, in questo caso A=2·6 e B=4·(-3) ovvero A=12 e B=-12. La somma algebrica dei prodotti è A+B=12+(-12)=0. Il risultato è nullo, quindi le due rette sono perpendicolari.

Dimostrazione

Considero due rette r e s in forma implicita.

$$ ax+by+c=0 $$

$$ a'x+b'y+c'=0 $$

I coefficienti angolari delle due rette sono:

$$ m = - \frac{a}{b} $$

$$ m' = - \frac{a'}{b'} $$

Quando due rette sono perpendicolari, il prodotto dei loro coefficienti angolari è uguale a -1.

$$ m \cdot m' = -1 $$

$$ m = \frac{-1}{m'} $$

Sostituisco m=-a/b e m=-a'/b'.

$$ - \frac{a}{b} = \frac{-1}{[ - \frac{a'}{b'} ]} $$

$$ - \frac{a}{b} = \frac{1}{\frac{a'}{b'}} $$

$$ - \frac{a}{b} = \frac{b'}{a'} $$

$$ - aa' = bb' $$

$$ - aa' - bb' = 0 $$

$$ (- aa' - bb') \cdot (-1) = 0 \cdot (-1) $$

$$ aa' + bb' = 0 $$

La condizione di perpendicolarità è dimostrata.

Retta perpendicolare al piano

Una retta \( r \) è perpendicolare al piano \( \alpha \) quando è incidente al piano ed è perpendicolare a tutte le rette del piano.

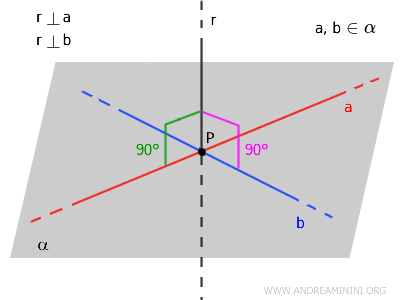
In altre parole, per essere perpendicolare a un piano \( \alpha \), una retta deve soddisfare due condizioni.

• La retta \( r \) interseca il piano \( \alpha \) in un punto qualsiasi, cioè è "incidente al piano".
• La retta \( r \) è perpendicolare a tutte le rette del piano \( \alpha \) che passano per il punto di intersezione.

Questa condizione equivale a dire che il vettore direttore della retta \( r \) è "parallelo al vettore normale" del piano \( \alpha \).

Una retta incidente al piano che non è perpendicolare è detta obliqua.

Osservazioni

Osservazioni e note aggiuntive sulle rette perpendicolari

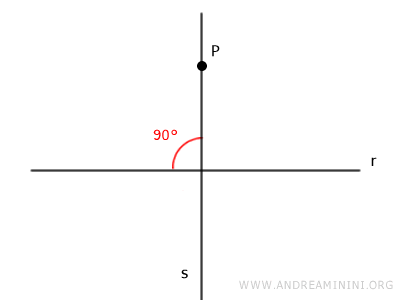
• Teorema della perpendicolare
  Dato un punto P e una retta r del piano, esiste una e una sola retta s passante per il punto P e perpendicolare alla retta r.
  
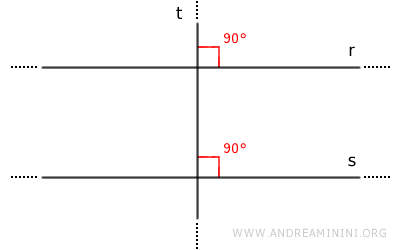
• Due rette r e s perpendicolari a una terza retta t sono rette parallele
  Le rette r e s formano coppie di angoli corrispondenti congruenti. Pertanto, per il teorema delle rette parallele sono rette parallele.
  
• Una retta t perpendicolare alla retta r è anche perpendicolare a tutte le parallele della retta r
  Date due rette parallele r e s, se la retta t è perpendicolare a una delle due rette r o s, allora è perpendicolare anche all'altra retta.
  

  Dimostrazione. Per ipotesi considero due rette parallele r//s e una terza retta t perpendicolare alla retta s. Quindi, le rette t e s formano un angolo retto (α=90°).
  
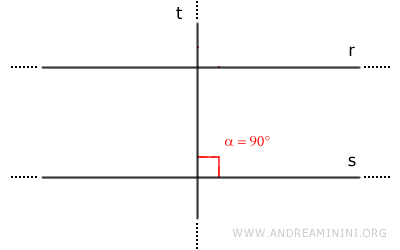
  Poiché le due rette r e s sono rette parallele r//s, per il teorema delle rette parallele le rette r e s formano coppie di angoli corrispondenti congruenti rispetto alla stessa retta trasversale (α≅β). Pertanto, anche l'angolo β è un angolo retto (β=90°).
  
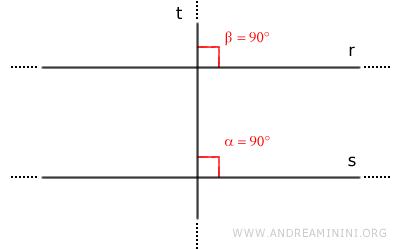
  Di conseguenza, la retta t è perpendicolare anche alla retta r.

• Le perpendicolari di due rette incidenti sono a loro volta rette incidenti
  Date due rette incidenti r e s, le rispettive rette perpendicolari p e q sono rette incidenti.
  

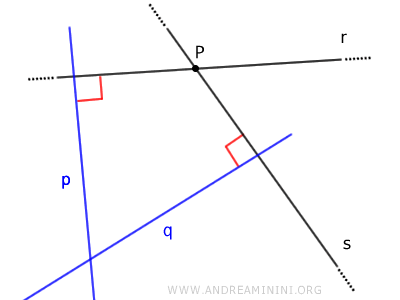
  Dimostrazione. Questa affermazione si dimostra per assurdo. Considero due rette incidenti r e s con le rispettive perpendicolari parallele p // q. Essendo p e q due rette parallele, per il teorema delle rette parallele gli angoli coniugati interni α e β rispetto a una retta trasversale t dovrebbero essere supplementari, ossia la loro somma dovrebbe essere pari a un angolo piatto (α+β=180°).
  
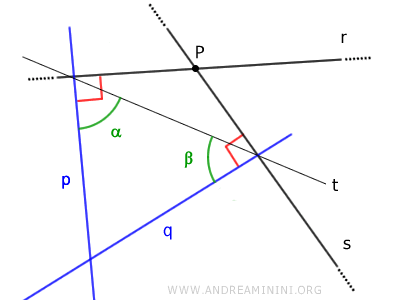
  In realtà, gli angoli α e β sono entrambi angoli acuti perché tagliano l'angolo retto (90°). Pertanto, la loro somma è inferiore a 180° e le rette p e q non sono parallele. Questo contraddice l'ipotesi iniziale. Di conseguenza, la tesi che due rette incidenti r e s abbiano perpendicolari parallele p//q è falsa. Quindi, è vera la sua negazione ovvero "due rette incidenti r e s hanno perpendicolari incidenti" nella parte in cui la somma degli angoli coniugati alfa più beta è inferiore a 180°

E così via.