Rette incidenti

Due o più rette distinte sono dette rette incidenti se si intersecano in un solo punto.

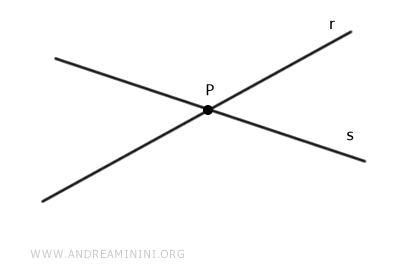
Due rette si intersecano quando hanno solo un punto in comune.

Questo accade perché tra due punti distinti può passare una e una sola retta.

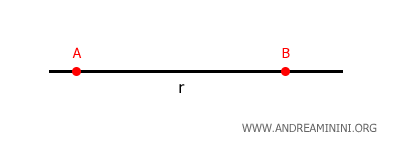
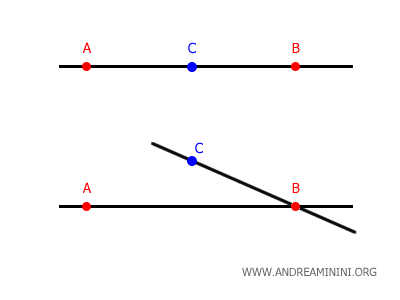
Quando due rette hanno più di un punto in comune sono rette coincidenti.

Pertanto, due rette possono essere incidenti solo se hanno un punto in comune.

L'intersezione di due rette divide il piano cartesiano in quattro parti, con due coppie di angoli opposti al vertice congruenti.

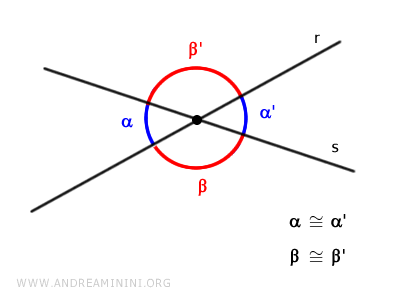
In base all'ampiezza degli angoli che dividono il piano le due rette incidenti sono dette:

• Rette perpendicolari
  Quando tutti e quattro gli angoli opposti al vertice sono congruenti, le due rette formano quattro angoli retti (90°) e sono dette rette perpendicolari.
  
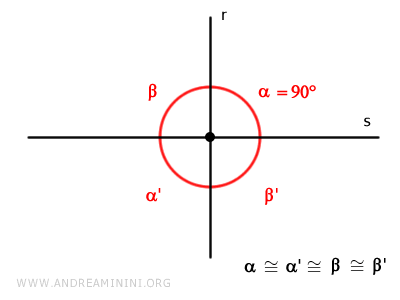
• Rette oblique
  Quando due rette incidenti non sono perpendicolari, sono dette rette oblique.
  

Come trovare il punto di intersezione delle rette sul piano

Nella geometria analitica, per individuare il punto in cui due rette incidenti si intersecano sul piano cartesiano, basta risolvere un sistema lineare a due equazioni. $$ \begin{cases} ax+by+c=0 \\ \\ a'x+b'y+c'=0 \end{cases} $$ Ogni equazione rappresenta una retta del piano.

La risoluzione del sistema di equazioni può portare a tre risultati:

• Il sistema ha un'unica soluzione. In questo caso il sistema è determinato e la soluzione è composta da due valori x e y che corrispondono alle coordinate (x;y) del punto di intersezione sul piano. Significa che le due rette sono incidenti e si intersecano in un punto specifico. Questo accade quando il rapporto tra i coefficienti "a" e "b" delle variabil x e y non è proporzionale, perché implica un diverso coefficiente angolare (m) delle due rette. $$ \frac{a}{a'} \ne \frac{b}{b'} \Longleftrightarrow m \ne m' $$
• Il sistema non ha nessuna soluzione. In questo caso il sistema è impossibile. Questo vuole dire che le rette non hanno punti in comune, ovvero non sono incidenti. Quindi, sono rette parallele e distinte. Questo accade quando i coefficienti "a" e "b" delle variabili x e y nelle due equazioni sono proporzionali, ma il termine "c" noto non lo è. $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$
• Il sistema ha infinite soluzioni. In questo caso il sistema è indeterminato. Questo significa che le rette hanno tutti i punti in comune, ovvero sono parallele e coincidenti. In altre parole, le due equazioni rappresentano la stessa retta. Questo accade quando i coefficienti il rapporto tra i coefficienti e dei termini noti delle due equazioni sono proporzionali. $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$

In questo modo è possibile usare l'algebra per conoscere il punto di intersezione tra due rette se esiste e la natura stessa delle rette: incidenti, parallele, coincidenti.

Esempio

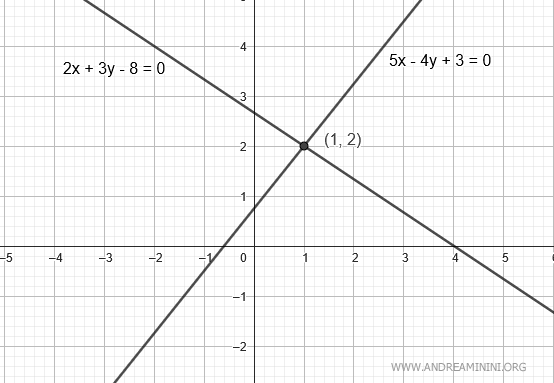
Considero due rette con le seguenti equazioni in forma implicita

$$ r: \ 2x+3y-8=0 $$

$$ r': \ 5x-4y+3=0 $$

Devo capire se sono incidenti, parallele o coincidenti.

Per farlo calcolo il rapporto dei coefficienti delle variabili x e y.

$$ \frac{a}{a'} = \frac{2}{5} $$

$$ \frac{b}{b'} = \frac{3}{4} $$

I rapporti sono diversi

$$ \frac{a}{a'} \ne \frac{b}{b'} $$

Quindi le rette sono incidenti.

Osservazioni

Alcune osservazioni sulle rette incidenti

• Se due rette a e b sono incidenti, sono incidenti anche le loro rispettive parallele a' e b'
  

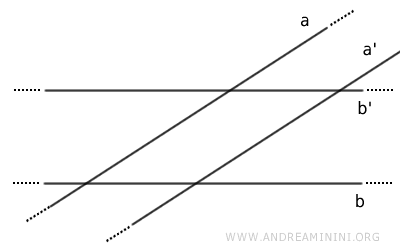
  Dimostrazione. Per assurdo, ipotizzo che sia vero il contrario. Date due rette a e b incidenti, le loro rispettive rette parallele a' e b' sono parallele tra loro a' // b' $$ a \parallel a' $$ $$ b \parallel b' $$ $$ a' \parallel b' $$ Tuttavia, se così fosse, per la proprietà transitiva dovrebbero essere parallele anche le rette a e b $$ a' \parallel b' \ , \ b' \parallel b \Rightarrow a \parallel b $$ Questo però contraddice l'ipotesi iniziale, in base alla quale le rette a e b sono incidenti. Quindi l'affermazione è falsa. E' vera la sua negazione, ossia date due rette a e b incidenti, sono incidenti anche le loro rispettive parallele a' e b'.

E così via