Il teorema di equivalenza di un triangolo e un poligono circoscritto a una circonferenza.
Un triangolo OHK e un poligono ABCDE (regolare o irregolare) circoscritto a una circonferenza sono equivalenti $$ ABCDE \doteq OHK $$ se l'altezza del triangolo è uguale al raggio della circonferenza e la base del triangolo è uguale al perimetro del poligono.
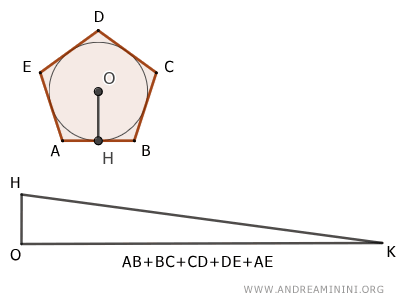
In termini geometrici, questo vuol dire che in un poligono circoscritto a una circonferenza, l'area può essere calcolata come se fosse un triangolo il cui altezza è il raggio della circonferenza e la base è il perimetro del poligono.
$$ Area = \frac{ perimetro \ × \ raggio}{2} $$
Sapendo che un poligono regolare è sempre circoscritto a una circonferenza, deduco che tutti i poligoni regolari sono equivalenti a un triangolo.
Solo alcuni poligoni irregolari, invece, sono circoscrivibili a una circonferenza.
In pratica, questo significa che l'area dei poligoni che soddisfano queste caratteristiche può essere calcolata come se fossero triangoli con specifiche misure nella base e nell'altezza. Per dimostrare questo teorema basta suddividere il poligono in tanti triangoli con l'altezza uguale al raggio della circonferenza.
Un esempio
Prendo come esempio un pentagono regolare ABCD in cui ogni lato è lungo 2.
Il pentagono circoscrive una circonferenza di raggio OH = 1,38.
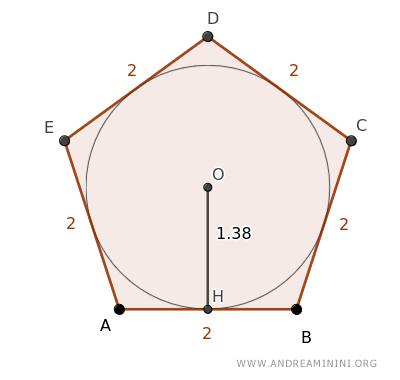
Essendo un poligono circoscritto a una circonferenza, posso applicare il teorema di equivalenza per calcolare la sua area come se fosse un triangolo.
Il perimetro del pentagono è P=10
$$ P = \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{AE} = 2+2+2+2+2 = 10 $$
Quindi considero un triangolo FGI di base FG=10 congruente al perimetro del poligono FG≅P e altezza IF=1,38 congruente al raggio della circonferenza IF≅OH.
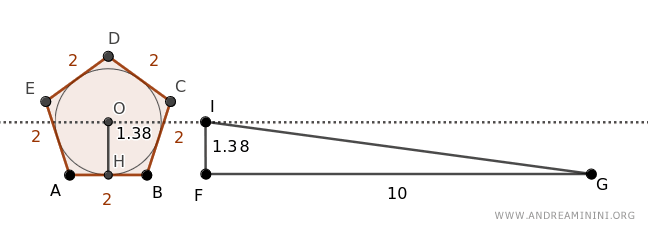
L'area del triangolo è uguale al semiprodotto della base per l'altezza.
$$ A_t = \frac{b \cdot h}{2} = \frac{10 \cdot 1,38}{2} = \frac{13,8}{2} = 6,9 $$
Pertanto, l'area del triangolo equivalente è 6,9
$$ A_t = 6,9 $$
Di conseguenza anche l'area del pentagono è 6,9
$$ A_p = A_t = 6,9 $$
In questo modo ho ottenuto l'area del pentagono senza doverla calcolare direttamente.
Per verificare il risultato, calcolo l'area del pentagono regolare usando la formula della geometria piana. $$ A_p = \frac{n \cdot l \cdot a}{2} $$ Dove n=5 è il numero dei lati del poligono regolare, l=2 è la lunghezza dei lati e a=1,38 è l'apotema. $$ A_p = \frac{5 \cdot 2 \cdot 1,38}{2} = \frac{13,8}{2} = 6,9 $$ Il calcolo è esattamente lo stesso.
La dimostrazione
Considero un poligono ABCDE circoscritto a una circonferenza con centro O e raggio OH.
E' indifferente il numero dei lati del poligono o che il poligono sia regolare o irregolare, l'importante è che circoscriva una circonferenza.
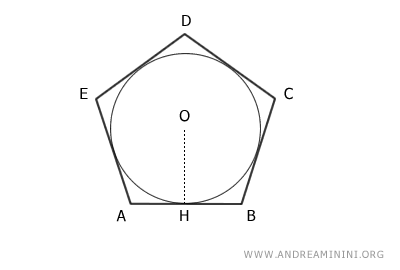
Il perimetro del poligono è la somma dei suoi lati
$$ P = \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{AE} $$
Congiungo il centro della circonferenza O con tutti i vertici del poligono.
In questo modo suddivido il poligono in cinque triangoli ABO, BCO, CDO, DEO, AEO
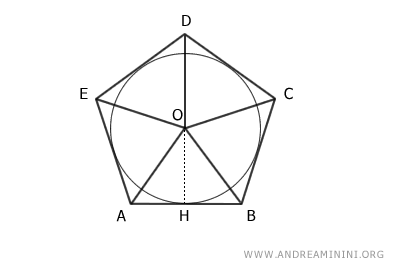
Aggiungo i segmenti che congiungono il centro della circonferenza O con i punti di intersezione tra la circonferenza e il poligono.
Essendo dei raggi, questi segmenti sono tutti congruenti con il segmento OH.
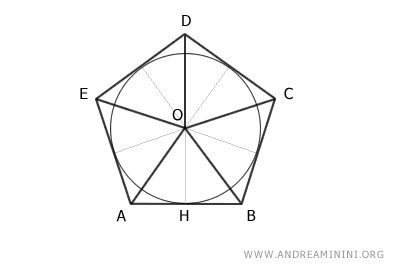
Pertanto, il poligono ABCDE è equivalente alla somma di cinque triangoli
$$ ABCDE \doteq ABO + BCO + CDO + DEO + AEO $$
Ora dispongo i lati del poligono su un'unica retta consecutivamente uno dopo l'altro.
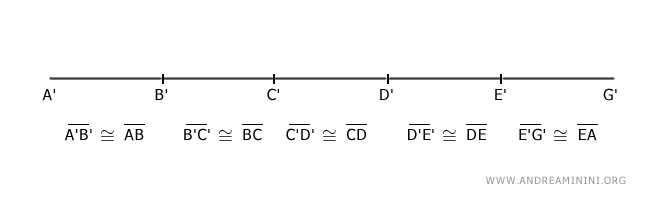
E' evidente che il segmento A'G' è congruente con il perimetro AB+BC+CD+DE+AE del poligono ABCDE.
$$ \overline{A'G'} \cong \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{AD} $$
Aggiungo all'estremo A' di A'G' un segmento perpendicolare A'F'≅OH congruente con il raggio della circonferenza (OH).
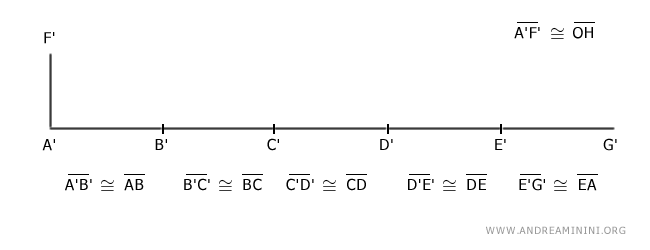
Infine traccio i segmenti che congiungono il punto F' con i punti B', C', D', E', G'.
In questo modo ottengo cinque triangoli.
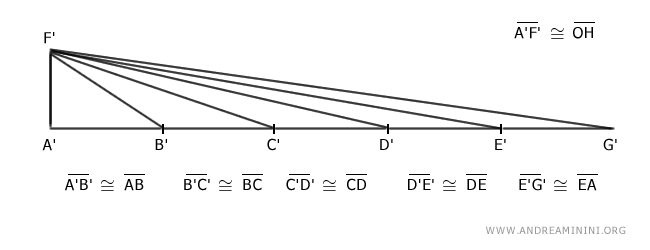
Per costruzione il triangolo A'G'F' ha per base il perimetro del poligono AB+BC+CD+DE+EA e per altezza A'F' il raggio della circonferenza inscritta nel poligono.
Inoltre, il triangolo A'G'F' è equivalente alla somma di cinque triangoli più piccoli.
$$ A'G'F' \doteq A'B'F' + B'C'F' + C'D'F' + D'E'F' + E'G'F' $$
In base al principio di equivalenza dei triangoli, i triangoli A'B'F' e ABO sono equivalenti, perché hanno la stessa altezza OH≅A'F' e la stessa base AB≅A'B'.
$$ A'B'F' \doteq ABO $$
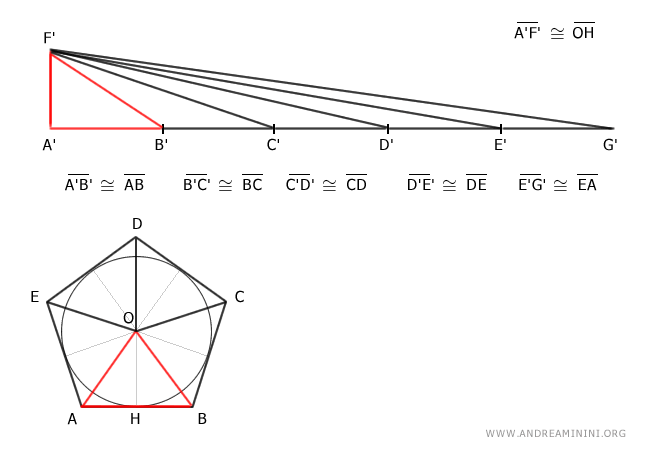
Per la stessa ragione sono equivalenti anche gli altri triangoli
$$ B'C'F' \doteq BCO $$
$$ C'D'F' \doteq CDO $$
$$ D'E'F' \doteq DEO $$
$$ E'G'F' \doteq AEO $$
So già che il triangolo A'G'F' è equivalente alla somma delle aree di cinque triangoli.
$$ A'G'F' \doteq A'B'F' + B'C'F' + C'D'F' + D'E'F' + E'G'F' $$
So anche che i triangoli che compongono A'G'F' sono equivalenti ai triangoli che compongono il poligono ABCDE. Quindi, i due poligoni sono poligoni equicomposti.
$$ A'G'F' \doteq ABO + BCO + CDO + DEO + AEO $$
$$ A'G'F' \doteq ABO + BCO + CDO + DEO + AEO \doteq ABCD $$
Pertanto deduco che il poligono ABCDE è equivalente al triangolo A'G'F' che ha per base il perimetro del poligono e per altezza il raggio della circonferenza inscritta nel poligono.
$$ A'G'F' \doteq ABCD $$
Questo dimostra che hanno la stessa area, ovvero sono equivalenti.
E così via.
