Asse di un segmento
L'asse di un segmento è la retta perpendicolare al segmento che passa per il suo punto medio.
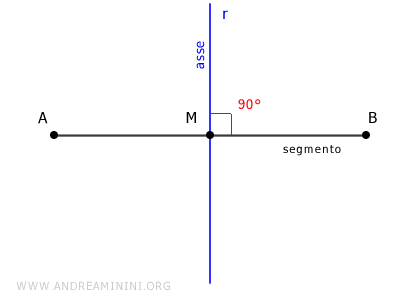
L'asse di un segmento è un luogo geometrico perché tutti i punti dell'asse sono equidistanti dagli estremi del segmento.
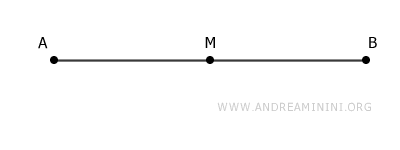
Ad esempio, considero il segmento AB

Il punto M è il punto medio del segmento AB perché divide il segmento a metà, creando due segmenti congruenti AM e MB.
L'asse del segmento AB è la retta r che interseca il segmento nel punto medio M ed è una retta perpendicolare al segmento stesso, ossia forma un angolo di 90°.

Come trovare l'equazione dell'asse di un segmento
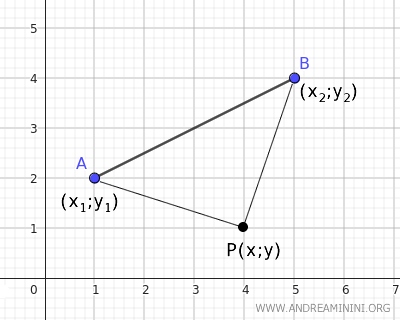
Per trovare l'equazione dell'asse di un segmento AB devo trovare i punti del piano P(x;y) che sono equidistanti dagli estremi A(x1;y1) e B(x2:y2) del segmento AB.
$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $
Esempio
Considero un segmento che ha per estremi i punti A(1;2) e B(5;4).
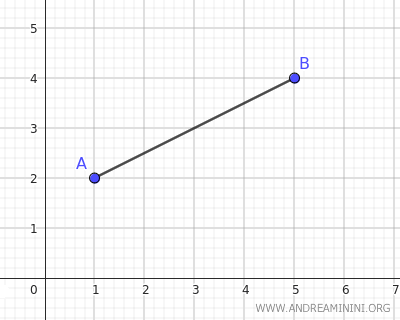
Per trovare l'equazione dell'asse cerco i punti del piano P(x;y) che soddisfano l'equidistanza dagli estremi A(1;2) e B(5:4) del segmento AB.
$$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $$
Sostituisco le coordinate dell'estremo A(1;2) nell'equazione ovvero x1=1 e y1=2.
$$ \sqrt{(y-2)^2 + (x-1)^2 } = \sqrt{(y-y_2)^2 + (x-x_2)^2} $$
Poi sostituisco anche le coordinate dell'estremo B(5;4) nell'equazione ovvero x2=5 e y2=4.
$$ \sqrt{(y-2)^2 + (x-1)^2 } = \sqrt{(y-4)^2 + (x-5)^2} $$
Entrambi i radicandi sono positivi, quindi posso elevare entrambi i membri dell'equazione al quadrato per semplificare il calcolo.
$$ ( \sqrt{(y-2)^2 + (x-1)^2 } )^2 = ( \sqrt{(y-4)^2 + (x-5)^2} )^2 $$
$$ (y-2)^2 + (x-1)^2 = (y-4)^2 + (x-5)^2 $$
Sviluppo i quadrati dei binomi.
$$ y^2 -4y+4 + x^2-2x+1 = y^2-8y+16 + x^2-10x+25 $$
Elimino i termini x2 e y2 da entrambi i lati dell'equazione.
$$ \require{cancel} \cancel{y^2} -4y+4 + \cancel{x^2}-2x+1 = \cancel{y^2}-8y+16 + \cancel{x^2}-10x+25 $$
Riordino e semplifico i termini.
$$-2x -4y+5 = -10x-8y+41 $$
$$-2x -4y+5 + 10x + 8y -41 = 0 $$
$$ 8x +4y-36 = 0 $$
Divido per quattro entrambi i lati dell'equazione per semplificare i coefficienti.
$$ \frac{8x +4y-36}{4} = \frac{0}{2} $$
$$ 2x +y-9 = 0 $$
Ho così trovato l'equazione della retta che identifica tutti i punti del piano equidistanti dagli estremi A e B del segmento AB, ovvero l'equazione dell'asse del segmento AB.
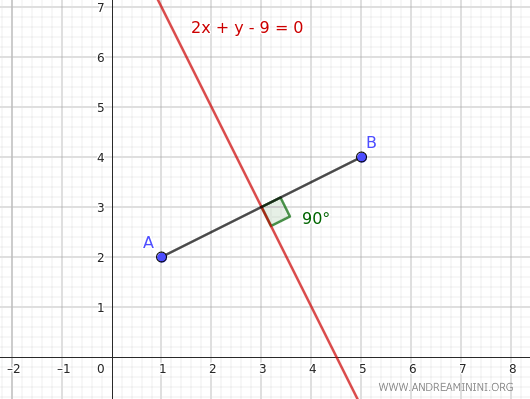
La retta che ho trovato passa per il punto medio del segmento AB formando un angolo retto.
Dimostrazione
Considero un segmento AB che ha per estremi i punti del piano A(x1;y1) e B(x2:y2). Devo trovare l'equazione dell'asse del segmento.
L'asse del segmento è un luogo geometrico composto dai punti del piano P(x;y) che sono equidistanti dagli estremi A e B del segmento AB.

Per trovare questi punti misuro la distanza di un generico punto P(x;y) del piano dagli estremi A(x1;y1) e B(x2;y2) del segmento AB.
- La distanza del punto P dall'estremo A del segmento
Il segmento PA misura la distanza di P dal punto A, posso calcolarlo usando il teorema di Pitagora sul triangolo ACP.
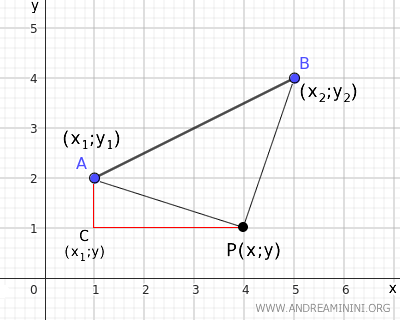
Dove il segmento PA è l'ipotenusa del triangolo rettangolo ACP. Sapendo che CP=|x-x1| e AC=|y-y1| $$ \overline{AP} = \sqrt{ \overline{AC}^2 + \overline{CP}^2} = \sqrt{(y-y_1)^2 + (x-x_1)^2} $$ - La distanza del punto P dall'estremo B del segmento
Il segmento PB misura la distanza di P dal punto B. Posso misurarla usando il teorema di Pitagora sul triangolo BDP.
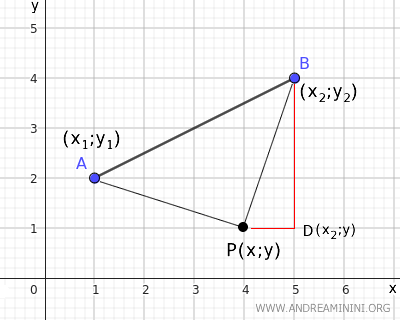
Dove il segmento PB è l'ipotenusa del triangolo rettangolo BDP. Sapendo che DP=|x-x2| e BD=|y-y2| $$ \overline{BP} = \sqrt{ \overline{AD}^2 + \overline{DP}^2} = \sqrt{(y-y_2)^2 + (x-x_2)^2} $$
Una volta trovata la distanza del punto P dagli estremi A e B del segmento, ovvero la lunghezza dei segmenti AP e BP, le eguaglio tra loro.
$$ \overline{AP} = \overline{BP} $$
$$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $$
Quest'ultima equazione mi permette di ricavare l'equazione dell'asse del segmento, conoscendo le coordinate degli estremi A(x1;y1) e B(x2;y2) del segmento AB.
Un metodo alternativo per trovare l'equazione dell'asse di un segmento
Per trovare l'asse del segmento posso considerare l'asse come la retta che passa per il punto medio del segmento in modo perpendicolare, ossia con un angolo retto di 90°.
Esempio
Considero lo stesso segmento dell'esempio precedente che ha per estremi i punti A(1;2) e B(5;4).

Per prima cosa devo trovare il punto medio del segmento facendo la media delle coordinate x e y dei due estremi A(1;2) e B(5;4).
$$ x_M = \frac{x_A+x_B}{2} = \frac{1+5}{2} = \frac{6}{2} = 3 $$
$$ y_M = \frac{y_A+y_B}{2} = \frac{2+4}{2} = \frac{6}{2} = 3 $$
Quindi, il punto medio del segmento AB si trova alle coordinate (xM;yM)=(3;3)
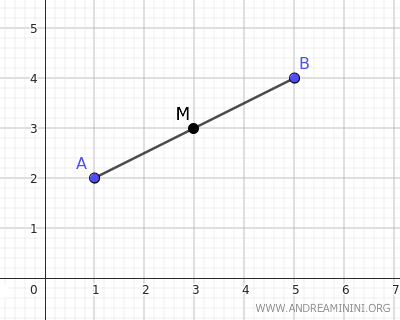
A questo punto ricostruisco l'equazione della retta coincidente con il segmento AB.
L'equazione della retta passante per due punti del piano A(x1;y1) e B(x2;y2) è la seguente:
$$ \frac{y-y_1}{y_2-y_1}= \frac{x-x_1}{x_2-x_1} $$
Sostituisco nell'equazione le coordinate dei punti A(1;2) e B(5;4) del segmento ossia x1=1, y1=2 e x2=5, y2=4.
$$ \frac{y-2}{4-2}= \frac{x-1}{5-1} $$
$$ \frac{y-2}{2}= \frac{x-1}{4} $$
$$ 4 \cdot (y-2)= 2 \cdot (x-1) $$
Semplifico le equazioni dividendo entrambi i lati per due.
$$ \frac{ 4 \cdot (y-2) }{2} = \frac{ 2 \cdot (x-1) }{2} $$
$$ 2 \cdot (y-2)= x-1 $$
$$ 2y-4= x-1 $$
Infine ricavo la y e ottengo l'equazione della retta che contiene il segmento AB
$$ 2y = x - 1 + 4 $$
$$ y = \frac{x+3}{2} $$
$$ y = \frac{x}{2} + \frac{3}{2} $$
Pertanto, la retta che passa per i punti A e B ha l'equazione y=x/2+3/2
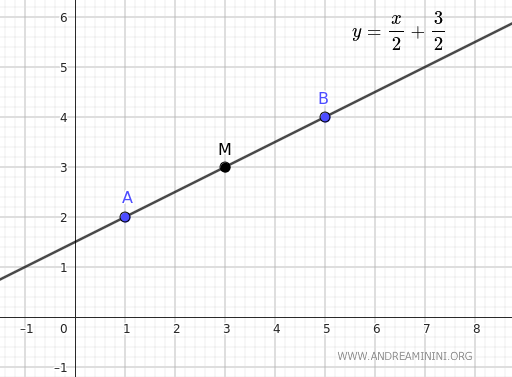
Guardando l'equazione della retta y=x/2+3/2 in forma impropria ottengo immediatamente il coefficiente angolare m della retta ovvero m=1/2
$$ m = \frac{1}{2} $$
A questo punto devo trovare l'equazione di una retta perpendicolare, ovvero che forma un angolo di 90°
$$ y' = m'x + c' $$
Secondo la condizione di perpendicolarità il prodotto dei coefficienti angolari m e m' di due rette perpendicolari è sempre -1
$$ m \cdot m' = -1 $$
Sostituisco il coefficiente angolare m=1/2 della retta che contiene il segmento AB che già conosco.
$$ \frac{1}{2} \cdot m' = -1 $$
E ottengo il coefficiente angolare m=2 della retta perpendicolare.
$$ m' = -2 $$
Quindi, l'equazione della retta perpendicolare ha coefficiente angolare m'=-2.
$$ y' = m'x + c' $$
$$ y' = -2x + c' $$
Per trovare il termine noto c', sostituisco nell'equazione y'=-2x+c' le coordinate del punto medio M(3;3) del segmento AB, ovvero x'=3 e y'=3
$$ 3 = -2 \cdot 3 + c' $$
$$ 3 = -6 + c' $$
$$ c'=9 $$
Una volta trovato il termine noto c'=9 lo sostituisco nell'equazione della retta perpendicolare.
$$ y' = -2x + c' $$
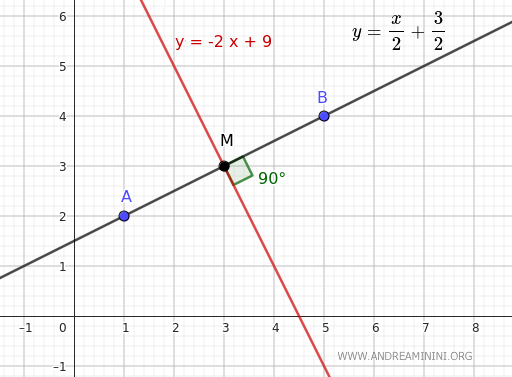
$$ y' = -2x + 9 $$
Ho così trovato la retta perpendicolare al segmento AB che passa per il punto medio M, ovvero l'equazione dell'asse del segmento AB.
Osservazioni
Alcune osservazioni e note
- Punti simmetrici rispetto all'asse
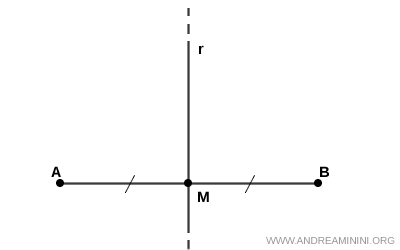
Dati due punti A e B che individuano un segmento AB, se una retta r è l’asse di questo segmento, allora i punti A e B si dicono simmetrici rispetto alla retta r.
- I punti dell'asse sono equidistanti dagli estremi del segmento
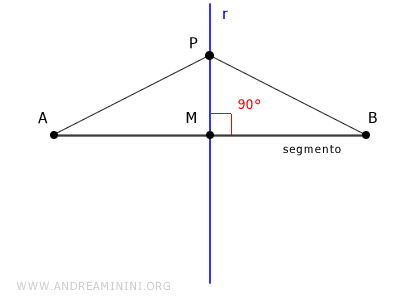
L'asse è un luogo geometrico perché tutti i suoi punti hanno la stessa distanza dagli estremi A e B del segmento.Dimostrazione. Considero un punto P dell'asse r del segmento AB. Devo dimostrare che P è equidistante dagli estremi A e B del segmento. Sapendo che r è l'asse del segmento AB, deduco che il punto di intersezione M è il punto medio di AB, quindi i segmenti AM e BM sono congruenti (AM≅BM). Quindi, per il primo principio di congruenza (LAL) i triangoli rettangolo AMP≅BMP sono congruenti, in quanto hanno un lato coincidente (MP), un lato congruente (AM≅AB) e l'angolo compreso tra i due lati congruente (90°). Essendo congruenti, i due triangoli hanno tutti i lati congruenti. Quindi, anche i segmenti AP≅BP sono congruenti.
Dimostrazione inversa. Si può dimostrare l'inverso. Se un punto P è equidistante dagli estremi A e B, allora è necessariamente un punto dell'asse P∈r. In questo caso l'ipotesi di partenza è l'equidistanza del punto P ossia AM≅BM e il fatto che la retta r sia l'asse del segmento AB. Devo dimostrare che il punto P equidistante dagli estremi A e B appartiene alla retta r. Per farlo basta osservare che il triangolo ABP è un triangolo isoscele perché ha due lati congruenti (AM≅BM). Essendo un triangolo isoscele, l'altezza corrisponde alla mediana. Quindi, il punto P appartiene sicuramente all'asse r, ossia alla retta perpendicolare al segmento AB che passa per il suo punto medio M.
E così via.
