La distanza tra due punti
La distanza è il percorso più breve per andare da un punto all'altro. Per misurare la distanza tra due punti del piano utilizzo il teorema di Pitagora $$ \overline{AB} = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} $$
Dove (x1,y1) e (x2,y2) sono le coordinate cartesiane dei punti A e B sul piano.
Un esempio pratico
Ecco le coordinate cartesiane di due punti nello spazio
$$ A = \begin{pmatrix} 2 \\ 4 \end{pmatrix} = (2;4) $$
$$ B = \begin{pmatrix} 6 \\ 1 \end{pmatrix} = (6;1) $$
La distanza tra i due punti è uguale a
$$ \overline{AB} = \sqrt{(6-2)^2+(1-4)^2} $$
$$ \overline{AB} = \sqrt{4^2+(-3)^2} = \sqrt{16+9}= \sqrt{25}=5 $$
Verifica con Geogebra. La distanza appena calcolata è confermata anche da Geogebra.
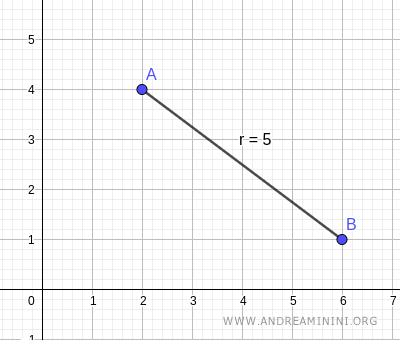
La dimostrazione
Considero due punti del piano
Il segmento AB misura la distanza tra i due punti A e B.
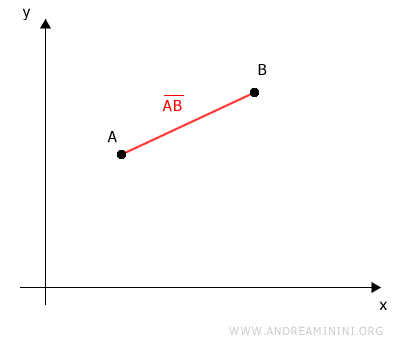
Proietto i due punti sugli assi cartesiani.
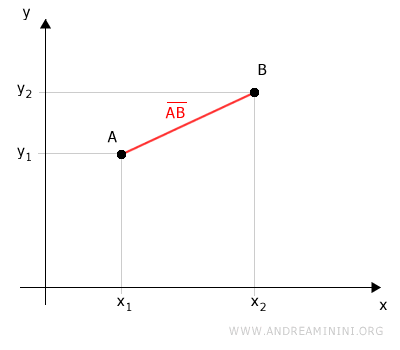
Le proiezioni tracciano sul piano un triangolo rettangolo ABC.
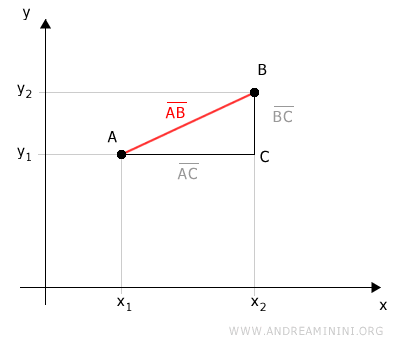
Il segmento AB è l'ipotenusa del triangolo rettangolo ABC.
Quindi, per misurare il segmento AB posso usare il teorema di Pitagora.
$$ \overline{AB} = \sqrt{\overline{AC}^2+\overline{BC}^2} $$
Il segmento AC è la proiezione del segmento AB sull'asse delle ascisse (x).
$$ \overline{AB} = \sqrt{(x_2-x_1)^2+\overline{BC}^2} $$
Il segmento BC è la proiezione del segmento AB sull'asse delle ordinate (y).
$$ \overline{AB} = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} $$
Il risultato è la formula che volevo dimostrare.
La distanza tra due punti nello spazio
Per due punti A $(x_A,\,y_A,\,z_A)$ e B $(x_B,\,y_B,\,z_B)$ nello spazio cartesiano, la distanza $AB$ è: $$ AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2}$$
La distanza tra due punti nello spazio coincide con la diagonale di un parallelepipedo costruito tramite le differenze assolute sugli assi: $|x_A-x_B|$, $|y_A-y_B|$, $|z_A-z_B|$.
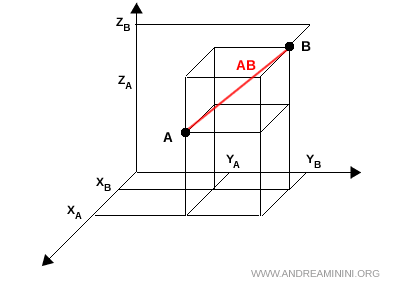
Quindi, per trovare la distanza tra i punti $ A $ e $ B $ si utilizza la stessa formula usata per calcolare la diagonale $ AB $ del parallelepipedo.
Nota. Quando uno dei due punti è l’origine $O(0,0,0)$, la stessa formula si riduce alla lunghezza del vettore posizione dell'altro punto. Ad esempio, per misurare la distanza del punto $ A $ dall'origine $ O $ la formula diventa $$ AO=\sqrt{x_A^2+y_A^2+z_A^2} $$
Esempio
Dati due punti $ A $ e $ B $ nello spazio
$$ A(2,\,-1,\,3)$$
$$ B(-2,\,4,\,0) $$
La distanza tra i due punti è
$$ AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2} $$
$$ AB=\sqrt{(2-(-2))^2+((-1)-4)^2+(3-0)^2} $$
$$ AB=\sqrt{4^2+(-5)^2+3^2} $$
$$ AB=\sqrt{16+25+9} $$
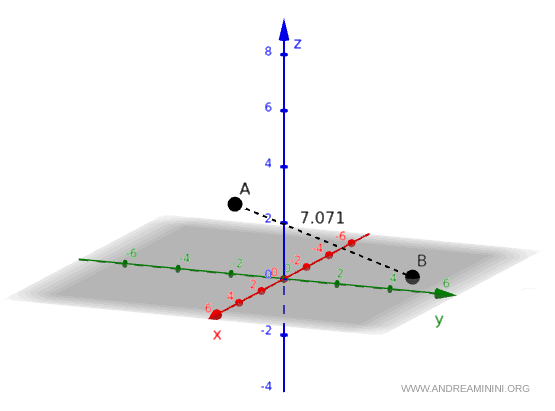
$$ AB=\sqrt{50} \approx 7,071 $$
Quindi, la distanza tra i due punti è $ \sqrt{50} $.
La distanza misurata con le coordinate polari
La distanza tra due punti del piano può essere misurata anche usando le coordinate polari dei due punti. $$ \overline{AB} = \sqrt{r_1^2+r_2^2-2r_1r_2 \cos (\alpha_2 - \alpha_1)} $$
Dove (r1,α1) e (r2,α2) sono le coordinate polari dei due punti sul piano.
Esempio
Due punti nel piano hanno le seguenti coordinate polari
$$ A [ \ 4.47 \ , \ 63.43° \ ] $$
$$ B [ \ 6.08 \ , \ 9.46° \ ] $$
Dal punto di vista grafico
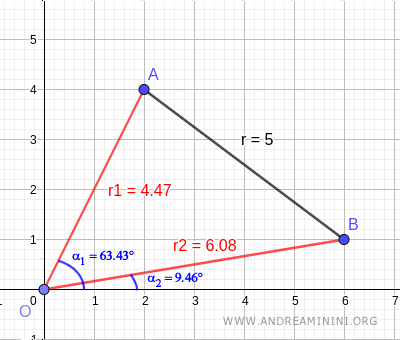
La distanza tra i due punti A e B è
$$ \overline{AB} = \sqrt{r_1^2+r_2^2-2r_1r_2 \cos (\alpha_2 - \alpha_1)} $$
$$ \overline{AB} = \sqrt{(4.47)^2+(6.08)^2-2 \cdot (4.47) \cdot (6.08) \cos ( 9.46° - 63.43°)} $$
$$ \overline{AB} = \sqrt{19.98+36.97- 54.36 \cdot \cos ( - 53.97°)} $$
$$ \overline{AB} = \sqrt{25} = 5 $$
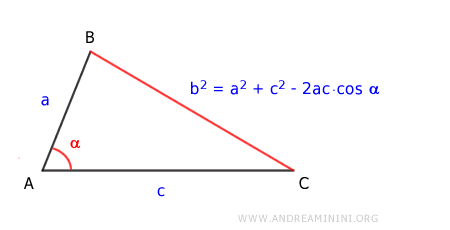
Dimostrazione. La formula distanza tra le coordinate polari è l'applicazione del teorema del coseno di un triangolo.
E così via.
