Rette passanti per un punto e tangenti alla circonferenza

Data una circonferenza, in ogni punto esterno P passano due rette tangenti con la circonferenza.


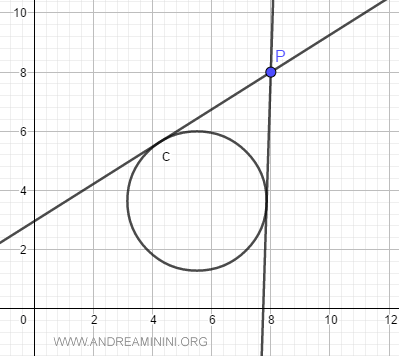
Nei punti della circonferenza, invece, passa una e una sola retta tangente.

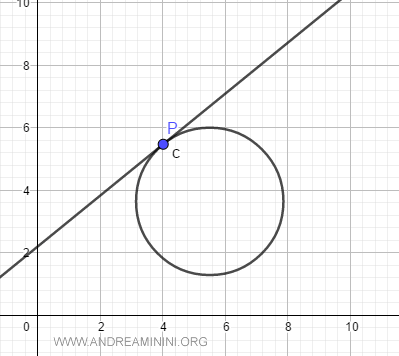
E nei punti interni?

Nei punti interni alla circonferenza non passa nessuna retta tangente.

Esempio

Ho una circonferenza C

$$ (x^2+y^2)−6x−4y+9=0 $$

Prendo un punto esterno alla circonferenza.

$$ P \begin{pmatrix} 1 \\ 6 \end{pmatrix} $$

Ecco la rappresentazione grafica

Devo trovare le rette passanti per P e tangenti con la circonferenza.

Essendo un punto esterno, esistono due rette tangenti alla circonferenza passanti per P.

Queste rette appartengono al fascio proprio di rette del punto P.

$$ y−y_0=m⋅(x−x_0) $$

Dove x₀ e y₀ sono le coordinate del punto P

$$ y−6=m⋅(x−1) $$

Quindi l'equazione generale delle rette passanti per P è

$$ m⋅(x−1) - y + 6 = 0 $$

Per individuare le rette tangenti, devo trovare il coefficiente angolare che determina le rette che hanno una distanza minima (d) dalla circonferenza pari al raggio (r) della circonferenza.

Come prima cosa calcolo il centro C e il raggio r della circonferenza.

$$ \begin{cases} x_0 = - \frac{a}{2} \\ y_0 = - \frac{b}{2} \\ r = \sqrt{x_0^2 + y_0^2 - c} \end{cases} $$

Dove a,b,c sono i coefficienti dell'equazione della circonferenza ( a=-6 , b=-4, c=9 ).

$$ \begin{cases} x_0 = - \frac{-6}{2} = 3 \\ y_0 = - \frac{-4}{2} = 2 \\ r = \sqrt{x_0^2 + y_0^2 - 9} \end{cases} $$

Quindi il centro C della circonferenza è il punto con coordinate (x₀,y₀) = (3,2)

Una volta trovato il centro posso calcolare il raggio della circonferenza

$$ \begin{cases} x_0 = - \frac{-6}{2} = 3 \\ y_0 = - \frac{-4}{2} = 2 \\ r = \sqrt{3^2 + 2^2 - 9} = \sqrt{4} = 2 \end{cases} $$

Il raggio della circonferenza (r) è uguale a 2.

A questo punto posso individuare le rette passanti per P con distanza minima dalla circonferenza uguale al raggio ( r=2 ).

$$ d(C(x_0,y_0),retta) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} = r $$

$$ d(C(x_0,y_0),retta) = \frac{|m⋅(x_0−1) - y_0 + 6 |}{\sqrt{a^2+b^2}} = 2 $$

Dove x₀ e y₀ sono le coordinate del punto centrale della circonferenza ( 3,2 ) mentre i coefficienti sono a=m e b=-1.

$$ \frac{|m⋅(3−1) - 2 + 6 |}{\sqrt{m^2+(-1)^2}} = 2 $$

$$ \frac{|m⋅(2) + 4 |}{\sqrt{m^2+1}} = 2 $$

$$ |2m + 4 | = 2 \cdot \sqrt{m^2+1} $$

Divido entrambi i membri dell'equazione per due

$$ \frac{|2m + 4 |}{2} = \frac{2 \cdot \sqrt{m^2+1}}{2} $$

$$ |m + 2 | = \sqrt{m^2+1} $$

Poi elevo entrambi i membri dell'equazione alla seconda

$$ |m + 2 |^2 = ( \sqrt{m^2+1} )^2 $$

$$ |m + 2 |^2 = (m^2+1) $$

Calcolo il quadrato del binomio

$$ |m^2 +4m +4| = (m^2+1) $$

Elimino m² da entrambi i membri

$$ |4m +4| = 1 $$

Infine, elimino il valore assoluto

$$ 4m +4 = ±1 $$

$$ 4m = ±1 - 4 $$

$$ m = \frac{ ±1 - 4 } {4} $$

Ottengo così due soluzioni:

$$ m = \begin{cases} \frac{ +1 - 4 } {4} = \frac{-3}{4} \\ \frac{ -1 - 4 } {4} = \frac{-5}{4} \end{cases} $$

E quindi ottengo le equazioni delle rette tangenti

$$ \frac{-3}{4}⋅(x−1) - y + 6 = 0 $$

$$ \frac{-5}{4}⋅(x−1) - y + 6 = 0 $$

Tuttavia, in alcuni casi il metodo non funziona

Come si può vedere dal grafico soltanto una delle due equazioni è effettivamente tangente alla circonferenza.

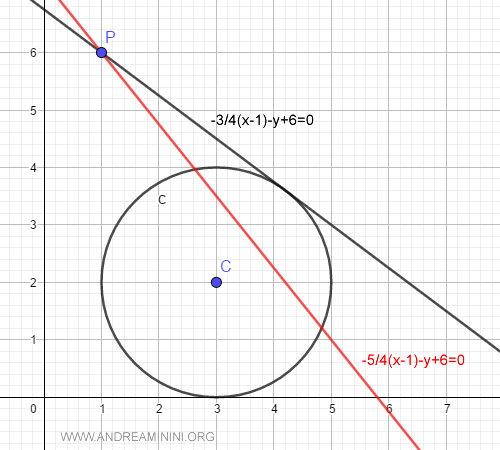
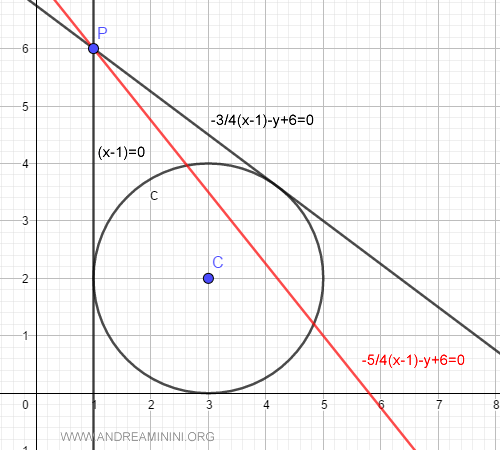
E' sempre opportuno verificare che una delle due rette tangenti non sia verticale.

In questi casi, l'equazione generale della retta non funziona.

Basta calcolare il valore assoluto della differenza tra il punto C e il punto P.

$$ | C - P | = | \begin{pmatrix} 3 \\ 2 \end{pmatrix} - \begin{pmatrix} 1 \\ 6 \end{pmatrix} | = \begin{pmatrix} | 3 - 1 | \\ | 2 - 6 | \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

Se il valore assoluto della differenza delle coordinate x è uguale al raggio, allora la retta tangente è verticale.

In questo caso la coordinata x è uguale al raggio r=2.

Pertanto, la seconda equazione della retta tangente è la seguente:

$$ x - x_0 = 0 $$

ossia

$$ x - 1 = 0 $$

L'altra retta tangente è perfettamente verticale.

E così via.