I punti interni ed esterni alla circonferenza
Punto interno alla circonferenza
Un punto P è interno alla circonferenza se la distanza tra il centro C della circonferenza e il punto P è minore del raggio (r) $$ d(C,P)<r $$
Punto esterno alla circonferenza
Un punto P è esterno alla circonferenza se la distanza tra il centro C della circonferenza e il punto P è maggiore del raggio (r) $$ d(C,P)>r $$
Se la distanza tra il punto P e il centro C della circonferenza è uguale, allora il punto si trova esattamente nella circonferenza.
Un esempio pratico
Ho la seguente equazione di una circonferenza
$$ x^2 + y^2 -4x +3y - 5 = 0 $$
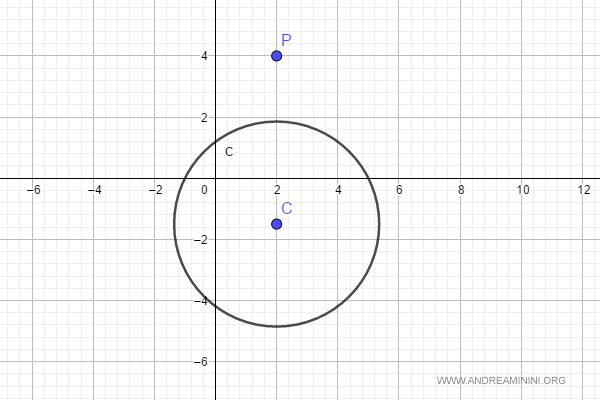
Voglio capire se il punto P è interno o esterno
$$ P \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
Per prima cosa calcolo il punto centrale C(x0,y0) della circonferenza sapendo che
$$ \begin{cases} a=−2x_0 \\ b=−2y_0 \end{cases} $$
In questo caso i coefficienti a e b sono
$$ a=-4 $$
$$ b=3 $$
$$ c =-5 $$
Quindi
$$ \begin{cases} a=−2x_0 \\ b=−2y_0 \end{cases} $$
$$ \begin{cases} -4=−2x_0 \\ 3=−2y_0 \end{cases} $$
$$ \begin{cases} x_0=2 \\ y_0=-\frac{3}{2} \end{cases} $$
Ho così ottenuto le coordinate del punto centrale della circonferenza
$$ C \begin{pmatrix} 2 \\ -\frac{3}{2} \end{pmatrix} $$
A questo punto calcolo anche il raggio
$$ \sqrt{x_0^2 + y_0^2 - c } = r $$
$$ \sqrt{2^2 + (-\frac{3}{2})^2 - (-5) } = r $$
$$ \sqrt{ 4 + \frac{9}{4} +5 }= r $$
$$ \sqrt{ \frac{9+36}{4} }= r $$
$$ \sqrt{ \frac{45}{4} }= r $$
$$ 3.35 = r $$
Ho trovato il raggio della circonferenza.
$$ r=3.35 $$
Poi calcolo la distanza tra il punto C e il punto P.
$$ d(P,C) = \sqrt{(x-x_0)^2+(y-y_0)^2} $$
$$ d(P,C) = \sqrt{(2-2)^2+(4-(-\frac{3}{2}))^2} $$
$$ d(P,C) = \sqrt{\frac{121}{4}} = 5.5 $$
Sapendo che il raggio della circonferenza è uguale a 3.35
Il punto P ha una distanza maggiore del raggio.
$$ d(P,C) = 5.5 > 3.35 = r $$
Pertanto, posso affermare che il punto P è un punto esterno alla circonferenza.
E così via.
