La distanza tra due punti, rette e piani nello spazio
I vari modi per misurare le distanze nello spazio a tre dimensioni.
La distanza tra due punti
Per misurare la distanza tra due punti nello spazio A e B, si calcola norma euclidea della differenza tra i due punti. $$ \overrightarrow{P_1,P_2} = \begin{Vmatrix}\begin{pmatrix} x_2-x_1 \\ y_2-y_1 \\ z_2-z_1 \end{pmatrix} \end{Vmatrix} $$ $$ = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2} $$
Esempio
Ecco le coordinate di due punti nello spazio
$$ P_1 = \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix} $$
$$ P_2 = \begin{pmatrix} 1 \\ 1 \\ -3 \end{pmatrix} $$
La distanza tra i due punti è uguale a
$$ \overrightarrow{P_1,P_2} = \begin{Vmatrix}\begin{pmatrix} 1-2 \\ 1-(-3) \\ -3-4 \end{pmatrix} \end{Vmatrix} $$ $$ = \begin{Vmatrix}\begin{pmatrix} -1 \\ 4 \\ -7 \end{pmatrix} \end{Vmatrix} = \sqrt{(-1)^2+(4)^2+(-7)^2} = \sqrt{66} = 8,12 $$
Verifica con Geogebra. La distanza appena calcolata è confermata anche da Geogebra.
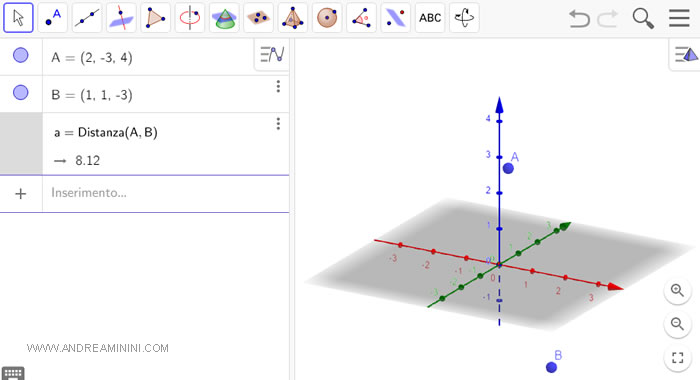
La distanza tra un punto e una retta
Ci sono diversi metodi per calcolare la distanza tra un punto e una retta nello spazio.
Uno tra questi consiste nel ricondurla al calcolo della distanza tra due punti.
Esempio
Nello spazio ho un punto P e una retta r.
$$ P = \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix} $$
$$ r: \begin{cases} x+ y +1 = 0 \\ x+2y-z +1= 0 \end{cases} $$
Ecco la rappresentazione grafica
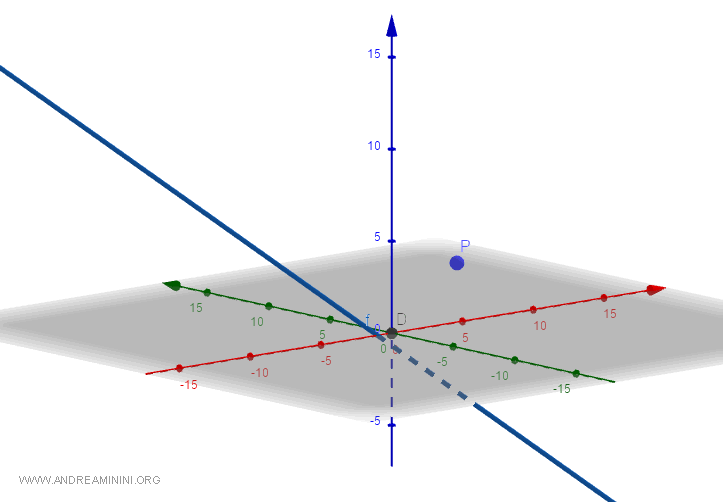
Trasformo l'equazione della retta da cartesiana a parametrica
$$ r: \begin{cases} x+ y +1 = 0 \\ x+2y-z +1= 0 \end{cases} $$
$$ r: \begin{cases} x= - y -1 = 0 \\ (-y-1)+2y-t +1= 0 \\ z=t \end{cases} $$
$$ r: \begin{cases} x = -1-t \\ y=t \\ z=t \end{cases} $$
Quindi, il vettore direttore della retta è
$$ v = \begin{pmatrix} -1 \\ 1 \\ 1 \end{pmatrix} $$
Calcolo l'equazione di un piano ortogonale alla retta r e passante per il punto P.
La generica equazione di un piano è
$$ ax + by + cz + d = 0 $$
Sostituisco i coefficienti a,b,c con i parametri del vettore direttore.
$$ (-1)x + (1)y + (1)z + d = 0 $$
$$ -x +y +z + d = 0 $$
Poi calcolo il coefficiente d inserendo al posto di x,y,z le coordinate del punto P
$$ -2 -3 + 4 + d = 0 $$
$$ -1 + d = 0 $$
$$ d = 1 $$
Quindi sostituisco d nell'equazione del piano e ho trovato il piano passante per P
$$ -x +y +z +1 = 0 $$
Ecco la rappresentazione grafica
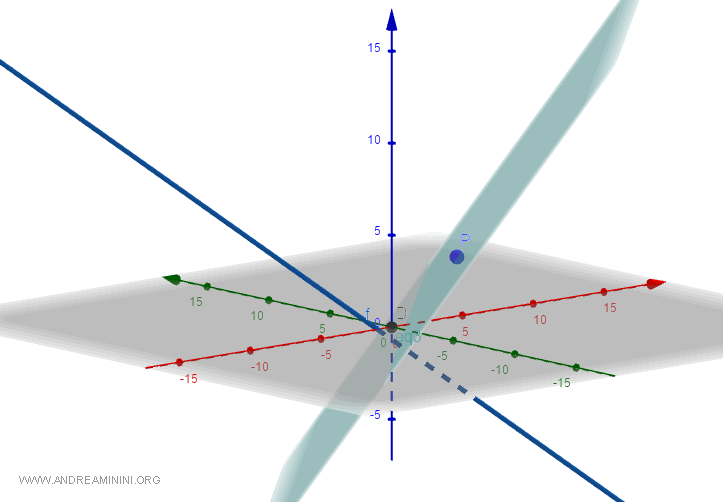
Ora devo trovare il punto di intersezione tra il piano e la retta.
Prendo le coordinate parametriche della retta
$$ r: \begin{cases} x = -1-t \\ y=t \\ z=t \end{cases} $$
e le sostituisco nell'equazione del piano.
$$ -x +y +z +1 = 0 $$
$$ -(-1-t) +t +t +1 = 0 $$
$$ 2+3t = 0 $$
$$ t = - \frac{2}{3} $$
Poi sostituisco il parametro t nell'equazione parametrica per trovare le coordinate (x,y,z) del punto di intersezione P'
$$ \begin{cases} x = -1-t \\ y=t \\ z=t \end{cases} $$
$$ \begin{cases} x = -1-(- \frac{2}{3}) \\ y=- \frac{2}{3} \\ z=- \frac{2}{3} \end{cases} $$
$$ \begin{cases} x = - \frac{1}{3} \\ y=- \frac{2}{3} \\ z=- \frac{2}{3} \end{cases} $$
Ho trovato le coordinate del punto P' della retta che interseca il piano perpendicolare passante per A.
$$ P' = \begin{pmatrix} - \frac{1}{3} \\ - \frac{2}{3} \\ - \frac{2}{3} \end{pmatrix} $$
Ecco la rappresentazione grafica
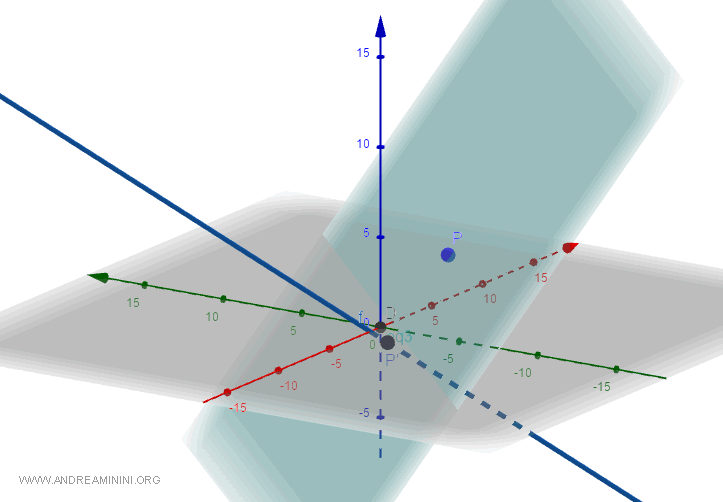
A questo punto posso calcolare la distanza tra i punti P e P'
$$ P = \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix} $$
$$ P' = \begin{pmatrix} - \frac{1}{3} \\ - \frac{2}{3} \\ - \frac{2}{3} \end{pmatrix} $$
$$ \overrightarrow{P,P'} = \begin{Vmatrix}\begin{pmatrix} - \frac{1}{3}-2 \\ - \frac{2}{3}-(-3) \\ - \frac{2}{3}-4 \end{pmatrix} \end{Vmatrix} $$ $$ = \begin{Vmatrix}\begin{pmatrix} - \frac{7}{3} \\ \frac{7}{3} \\ \frac{-14}{3} \end{pmatrix} \end{Vmatrix} = \sqrt{(- \frac{7}{3})^2+(- \frac{7}{3})^2+(\frac{14}{3})^2} = $$ $$ \sqrt{ \frac{49}{9}+ \frac{49}{9} +\frac{196}{9}} = \sqrt{ \frac{294}{9}} = 5.7154 $$
Ho così trovato la distanza minima tra la il punto e la retta nello spazio.
La distanza tra un punto e un piano
La distanza minima tra un punto P e un piano a nello spazio si calcola trovando la retta perpendicolare al piano a che passa per P. $$ d(P,a) = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} $$
Esempio
Ho un punto P nello spazio
$$ P = \begin{pmatrix} 1 \\ 3 \\ 2 \end{pmatrix} $$
e l'equazione cartesiana di un piano
$$ 4x-2y+z-5 = 0 $$
La distanza minima tra il punto e il piano è
$$ d(P,a) = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} $$
$$ d(P,a) = \frac{|4(1)-2(3)+1(2)-5|}{\sqrt{4^2+(-2^2)+1^2}} $$
$$ d(P,a) = \frac{|-5|}{\sqrt{21}} = \frac{5}{\sqrt{21}} = 1,09 $$
Ho così trovato la distanza tra il punto P e il piano.
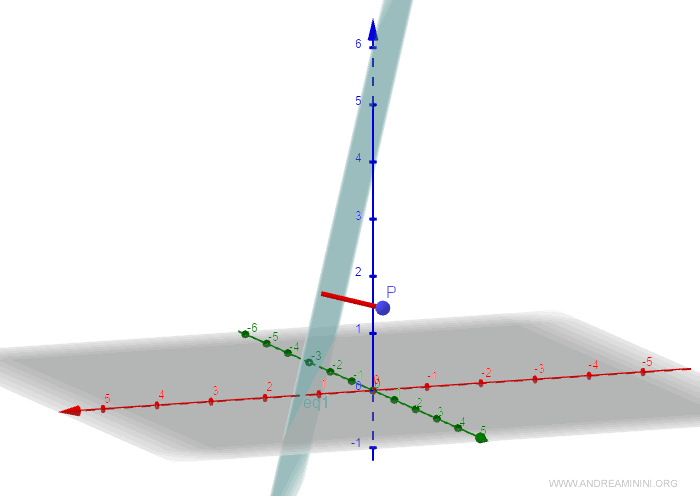
Quali sono le coordinate del punto sul piano?
Per calcolare le coordinate del punto H sul piano, devo prima trovare l'equazione della retta perpendicolare rH al piano che passa per il punto P.
Il vettore direttore della retta coincide con i parametri di giacitura a,b,c.
$$ r_H: \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \\ 2 \end{pmatrix} + t \begin{pmatrix} a \\ b \\ c \end{pmatrix} $$
$$ r_H: \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \\ 2 \end{pmatrix} + t \begin{pmatrix} 4 \\ -2 \\ 1 \end{pmatrix} $$
Per trovare il punto della retta che interseca il piano metto le equazioni in un unico sistema.
$$ \begin{cases} x = 1+4t \\ y=3-2t \\ z=2+t \\ 4x-2y+z-5 = 0 \end{cases} $$
Poi risolvo il sistema per sostituzione.
$$ 4x-2y+z-5 = 0 $$
$$ 4(1+4t)-2(3-2t)+(2+t)-5 = 0 $$
$$ 4+16t-6+4t+2+t-5 = 0 $$
$$ -5+21t = 0 $$
$$ t = \frac{5}{21} = 0.238 $$
Trovato il parametro t=0,38 posso calcolare le coordinate (x,y,z) del punto H.
$$ \begin{cases} x = 1+4t \\ y=3-2t \\ z=2+t \end{cases} $$
$$ \begin{cases} x = 1+4(0.238) \\ y=3-2(0.238) \\ z=2+0.238 \end{cases} $$
$$ \begin{cases} x = 1,952 \\ y=2,524 \\ z=2,238 \end{cases} $$
Ho trovato le coordinate del punto H sul piano.
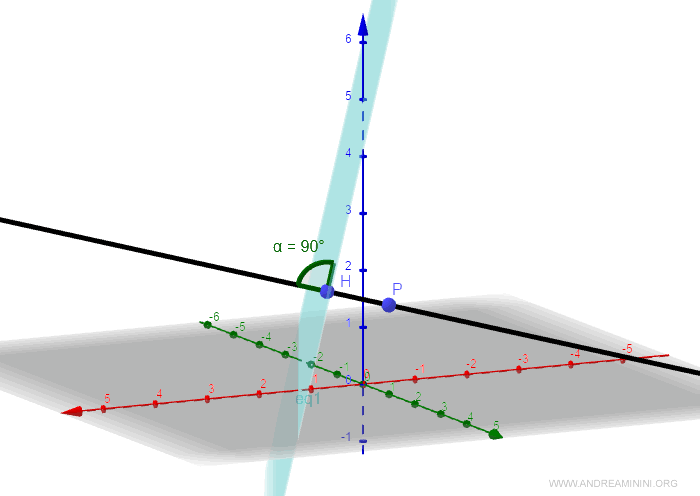
La distanza tra due piani
La distanza minima tra due piani α e β è sempre uguale a zero se i due piani sono incidenti o paralleli coincidenti. Se i due piani sono paralleli e distinti, dato un punto qualsiasi Pα(x0,y0,z0) del primo piano α si usa la seguente formula considerando i coefficienti dell'equazione cartesiana del secondo piano β $$ d(p_1,p_2) = \frac{ax_0+by_0+c_0+d}{\sqrt{a^2+b^2+c^2} } $$
Un esempio pratico
Ho due piani nello spazio a tre dimensioni
$$ -x-2y+z+1=0 $$
$$ 3x+6y-3z+4=0 $$
Verifico se sono incidenti.
Sono incidenti se i vettori direttori o normali sono linearmente indipendenti.
Calcolo il rango dei coefficienti delle equazioni dei piani.
$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{pmatrix} $$
$$ r_k \begin{pmatrix} -1 & -2 & 1 \\ 3 & 6 & -3 \end{pmatrix} =1 $$
Il rango è uguale a 1.
E' minore di 2. Quindi sono linearmente dipendenti. Non possono essere incidenti.
Pertanto sono piani paralleli.
Nota. Se fossero stati piani incidenti l'esercizio si sarebbe concluso qui. La distanza tra due piani incidenti è sempre zero.
Ora devo verificare se i due piani sono incidenti o distinti.
Prendo un punto qualsiasi del primo piano e verifico se appartiene anche al secondo piano.
Ad esempio, metto a zero la x e la y nel primo piano per calcolare z.
$$ -x-2y+z+1=0 $$
$$ z+1=0 $$
$$ z=-1 $$
Quindi, il punto sul primo piano ha le seguenti coordinate:
$$ P = \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} $$
Verifico se il punto P appartiene anche al secondo piano.
Sostituisco i valori delle coordinate di P alle incognite dell'equazione del secondo piano.
$$ 3x+6y-3z+4=0 $$
$$ 3(0)+6(0)-3(-1)+4=0 $$
$$ 7=0 $$
L'equazione non è verificata. Quindi il punto P non appartiene al secondo piano.
Sono piani paralleli e distinti.
Nota. Se fossero stati piani paralleli coincidenti l'esercizio si sarebbe concluso qui. La distanza tra due piani paralleli e coincidenti è sempre zero.
A questo punto, per calcolare la distanza tra i due piani uso la formula.
$$ d(p_1,p_2) = \frac{ax_0+by_0+c_z0+d}{\sqrt{a^2+b^2+c^2} } $$
$$ d(p_1,p_2) = \frac{a(0)+b(0)+c(-1)+d}{\sqrt{a^2+b^2+c^2} } $$
$$ d(p_1,p_2) = \frac{3(0)+6(0)-3(-1)+4}{\sqrt{3^2+6^2+(-3^2)} } $$
$$ d(p_1,p_2) = \frac{7}{\sqrt{54} } = 0.95 $$
I due piani paralleli distano tra loro 0,95.
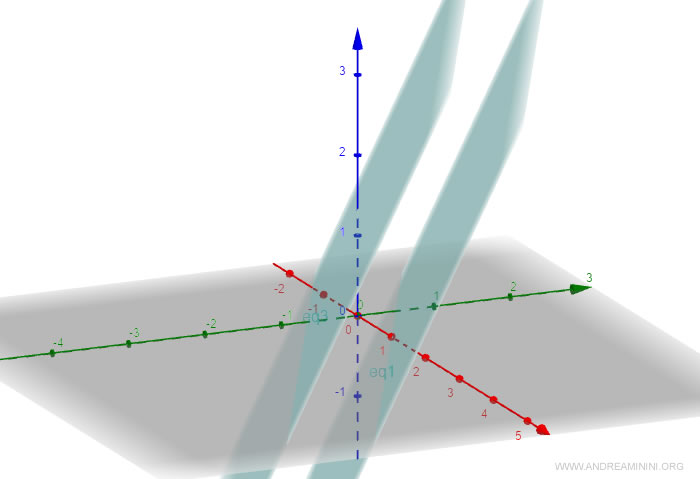
La distanza tra un piano e una retta
La distanza D(a,r) tra un piano e una retta è nulla se la retta è incidente o parallela coincidente al piano. Se la retta è parallela e distinta, preso un qualsiasi punto P della retta la distanza si ottiene con la seguente formula: $$ d(P,a) = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+b^2}} $$
Esempio
Ho un piano e una retta
$$ α :-2x-4y+2z+5=0 $$
$$ r: \begin{cases} x+ y +1 = 0 \\ x+2y-z +1= 0 \end{cases} $$
Verifico se la retta è parallela o incidente al piano tramite lo studio della linearità dei vettori normali.
$$ r : \begin{pmatrix} -2 & -4 & 2 \\ 1 & 1 & 0 \\ 1 & 2 & -1 \end{pmatrix} = 0 $$
Il rango della matrice dei vettori normali è uguale a 0.
Quindi la retta e il piano sono paralleli.
Per capire se sono coincidenti o distinti, prendo un punto qualsiasi del piano e verifico se appartiene anche alla retta.
Ad esempio, metto a zero le coordinate x,y per determinare z.
$$ -2x-4y+2z+5=0 $$
$$ -2(0)-4(0)+2z+5=0 $$
$$ z=\frac{-5}{2} $$
Quindi le coordinate del punto P sul piano sono
$$ \begin{pmatrix} 0 \\ 0 \\ \frac{-5}{2} \end{pmatrix} $$
Sostituisco le coordinate (x,y,z) del punto P del piano nella retta.
$$ r: \begin{cases} x+ y +1 = 0 \\ x+2y-z +1= 0 \end{cases} $$
$$ r: \begin{cases} 0+ 0 +1 = 0 \\ 0+2(0)-(\frac{-5}{2}) +1= 0 \end{cases} $$
$$ r: \begin{cases} 1 = 0 \\ \frac{5}{2} = -1 \end{cases} $$
Il punto non è compreso nella retta.
Pertanto, il piano e la retta sono paralleli e distinti.
A questo punto, trasformo l'equazione della retta in parametrica.
$$ r: \begin{cases} x+ y +1 = 0 \\ x+2y-z +1= 0 \end{cases} $$
$$ r: \begin{cases} x= -1-y \\ (-1-y)+2y-t +1= 0 \\ z=t \end{cases} $$
$$ r: \begin{cases} x= -1-t \\ y = t \\ z=t \end{cases} $$
Con t=0 trovo un punto P della retta.
$$ P = \begin{pmatrix} -1 \\ 0 \\ \frac{-5}{2} \end{pmatrix} $$
A questo punto applico la formula per calcolare la distanza tra il punto e il piano nello spazio.
$$ d(P,a) = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+b^2}} $$
$$ d(P,a) = \frac{|-2(x_0)-4(y_0)+2(z_0)+5|}{\sqrt{(-2)^2+(-4)^2+2^2}} $$
$$ d(P,a) = \frac{|-2(-1)-4(0)+2(0)+5|}{\sqrt{24} } $$
$$ d(P,a) = \frac{|7|}{\sqrt{24} } = 1,43 $$
Ho trovato la distanza tra la retta e il piano.
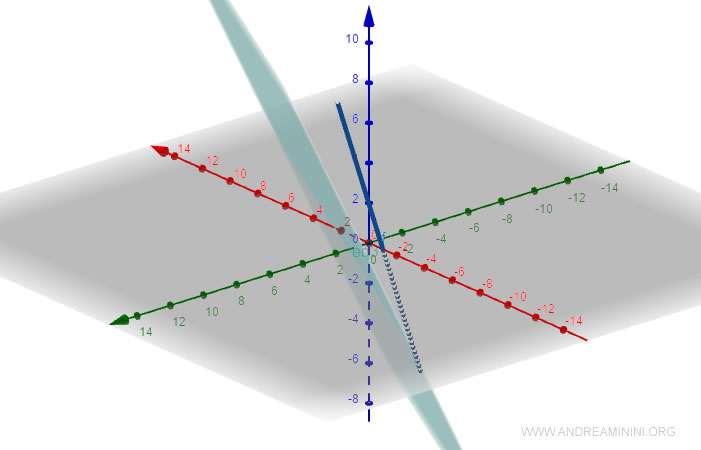
La distanza tra due rette nello spazio
- La distanza tra due rette r1 e r2 nello spazio si calcola a seconda della posizione delle due rette nello spazio.
- Se le rette sono incidenti, la distanza è ovviamente nulla. $$ d(r_1,r_2)=0 $$
- Se le rette sono parallele, la distanza si calcola prendendo una retta e un punto qualsiasi dell'altra retta. $$ d(P,r_2) = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} $$
- Se le rette sono sghembe,
Metodo 1
si trova il piano parallelo a entrambe le rette che passa per una di esse, poi si calcola la differenza tra il piano e l'altra retta $$ d(a,r_2) $$
Metodo 2
Si trova la retta perpendicolare e incidente a entrambe le rette. Poi si misura la distanza tra i due punti di intersezione.
Esempio ( metodo 1 )
Ho le equazioni cartesiane di due rette nello spazio
$$ r_1: \begin{cases} -x+y+z=1 \\ x+y+z=1 \end{cases} $$
$$ r_2: \begin{cases} x-y-2z=1 \\ -x-y+z=1 \end{cases} $$
Le trasformo in un sistema lineare
$$ \begin{cases} -x+y+z=1 \\ x+y+z=1 \\x-y-2z=1 \\ -x-y+z=1 \end{cases} $$
Calcolo il rango della matrice dei coefficienti A
$$ r_A \begin{pmatrix} -1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & -1 & -2 \\ -1 & -1 & 1 \end{pmatrix} = 3 $$
Il rango della matrice completa A|B è il seguente
$$ r_{A|B} \begin{pmatrix} -1 & 1 & 1 & 1 \\1 & 1 & 1 & 1 \\ 1 & -1 & -2 & 1 \\ -1 & -1 & 1 & 1 \end{pmatrix} = 4 $$
Il rango di A non coincide con il rango di A|B.
Quindi, il sistema non ha soluzioni e le due rette sono sghembe perché il rango di A|B è 4.
Il fascio di piani della prima retta è
$$ -x+y+z-1 + k (x+y+z-1 )=0 $$
$$ -x+y+z-1 + kx+ky+kz-k )=0 $$
$$ x(-1+k)+y(1+k)+z(1+k)-1-k =0 $$
Devo trovare il parametro k che includa anche l'altra retta.
Il vettore direttore della retta r2 è
$$ r_2: \begin{cases} x-y-2z=1 \\ -x-y+z=1 \end{cases} $$
$$ r_2: \begin{cases} x=y+2t+1 \\ -(y+2t+1)-y+t=1 \\ z=t \end{cases} $$
$$ r_2: \begin{cases} x=y+2t+1 \\ y=\frac{-2-t}{2} \\ z=t \end{cases} $$
$$ r_2: \begin{cases} x= ( \frac{-2-t}{2} )+2t+1 \\ y=\frac{-2-t}{2} \\ z=t \end{cases} $$
$$ r_2: \begin{cases} x= \frac{3t}{2} \\ y=\frac{-2-t}{2} \\ z=t \end{cases} $$
$$ r_2: \begin{cases} x= \frac{3}{2}t \\ y=-1-\frac{1}{2}t \\ z=t \end{cases} $$
Quindi il vettore direttore della retta r2 è
$$ v_{r2} = \begin{pmatrix} \frac{3}{2} \\ -\frac{1}{2} \\ 1 \end{pmatrix} $$
Secondo le condizioni di ortogonalità il piano passa per la retta r2 se il prodotto scalare tra il vettore normale del piano e il vettore direttore della retta è nullo.
Il vettore normale del fascio di piani è
$$ x(-1+k)+y(1+k)+z(1+k)-1-k =0 $$
$$ n_p = \begin{pmatrix} -1+k \\ 1+k \\ 1+k \end{pmatrix} $$
Quindi
$$ < v_{r2} , n_p> = 0 $$
$$ < \frac{3}{2}(-1+k) -\frac{1}{2} (1+k) +1 (1+k ) > = 0 $$
$$ -\frac{3}{2} +\frac{3}{2}k -\frac{1}{2} -\frac{1}{2} k +1+k = 0 $$
$$ k = \frac{1}{2} $$
Una volta trovato il valore di k lo sostituisco nell'equazione del piano.
$$ x(-1+k)+y(1+k)+z(1+k)-1-k =0 $$
$$ x(-1+\frac{1}{2})+y(1+\frac{1}{2})+z(1+\frac{1}{2})-1-\frac{1}{2} =0 $$
$$ x(-\frac{1}{2})+y(\frac{3}{2})+z(\frac{3}{2})-\frac{3}{2} =0 $$
Poi scelgo le coordinate (x,y,z) di un punto qualsiasi sulla retta r2.
Essendo il piano parallelo alla retta r2, ogni punto della retta ha la stessa distanza dal piano.
Ad esempio, metto a zero la z per determinare la x e la y.
$$ r_2: \begin{cases} x-y-2z=1 \\ -x-y+z=1 \end{cases} $$
$$ r_2: \begin{cases} x=1+y \\ -(1+y)-y=1 \end{cases} $$
$$ r_2: \begin{cases} x=0 \\ y=-1 \end{cases} $$
Quindi, le coordinate di un punto della retta sono (0, -1, 0).
$$ P = \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} $$
Ora calcolo la distanza tra il punto P sulla retta e il piano appena trovato
$$ \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} $$
$$ \frac{|-\frac{1}{2}x_0+\frac{3}{2}y_0+\frac{3}{2}z_0-\frac{3}{2}|}{\sqrt{-\frac{1}{2}^2+\frac{3}{2}^2+\frac{3}{2}^2}} $$
$$ \frac{|-\frac{1}{2} \cdot 0 +\frac{3}{2} \cdot (-1) +\frac{3}{2} \cdot 0 -\frac{3}{2}|}{\sqrt{ \frac{19}{4} }} $$
$$ \frac{| -3 |}{\sqrt{ \frac{19}{4} }} = 1,37 $$
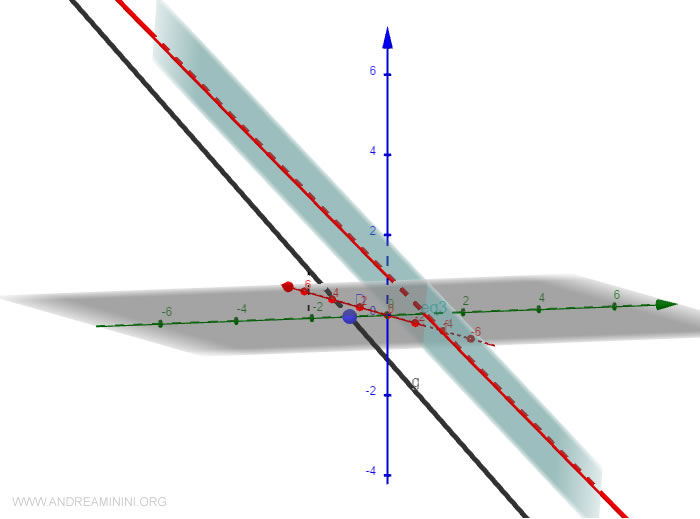
Esempio ( metodo 2 )
Ho le equazioni cartesiane di due rette nello spazio
$$ r_1: \begin{cases} -x+y+z=1 \\ x+y+z=1 \end{cases} $$
$$ r_2: \begin{cases} x-y-2z=1 \\ -x-y+z=1 \end{cases} $$
Calcolo il vettore direttore v della retta r1
$$ r_1: \begin{cases} -x+y+z=1 \\ x+y+z=1 \end{cases} $$
$$ r_1: \begin{cases} -x+y+t=1 \\ x+y+t=1 \\ z=t \end{cases} $$
$$ r_1: \begin{cases} -x+(1-t-x)+t=1 \\ y=1-t-x \\ z=t \end{cases} $$
$$ r_1: \begin{cases} -2x=0 \\ y=1-t-x \\ z=t \end{cases} $$
$$ r_1: \begin{cases} x=0 \\ y=1-t \\ z=t \end{cases} $$
Quindi, il vettore direttore della retta 1 è
$$ v_{r1} = \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix} $$
Un generico punto H1 della retta r1 è
$$ H_{r1} = \begin{pmatrix} 0 \\ 1-t \\ t \end{pmatrix} $$
Nota. Nell'insieme della retta c'è anche il punto di intersezione con l'altra retta per un determinato valore del parametro t.
Calcolo il vettore direttore v della retta r2
$$ r_2: \begin{cases} x-y-2z=1 \\ -x-y+z=1 \end{cases} $$
$$ r_2: \begin{cases} x-(-1+t-x)-2t=1 \\ y=-1+t-x \\ z=t \end{cases} $$
$$ r_2: \begin{cases} x=\frac{3}{2}t \\ y=-1+t-(\frac{3}{2}t) \\ z=1 \end{cases} $$
$$ r_2: \begin{cases} x=\frac{3}{2}t \\ y=-1-\frac{1}{2}t \\ z=1 \end{cases} $$
Quindi il vettore direttore della retta 2 è
$$ v_{r2} = \begin{pmatrix} \frac{3}{2} \\ -\frac{1}{2} \\ 1 \end{pmatrix} $$
Un generico punto H2 della retta r2 è
$$ H_{r2} = \begin{pmatrix} \frac{3}{2}t \\ -1-\frac{1}{2}t \\ t \end{pmatrix} $$
Ora, il segmento che congiunge i punti generici H1 e H2 è il seguente:
$$ \overrightarrow{H_{r1}H_{r2}} = \begin{pmatrix} \frac{3}{2}t_1 \\ -1-\frac{1}{2}t_1 \\ t_1 \end{pmatrix} - \begin{pmatrix} 0 \\ 1-t_2 \\ t_2 \end{pmatrix} $$
$$ \overrightarrow{H_{r1}H_{r2}} = \begin{pmatrix} \frac{3}{2}t_1 \\ -1-\frac{1}{2}t_1-1+t_2 \\ t_1-t_2\end{pmatrix} $$
$$ \overrightarrow{H_{r1}H_{r2}} = \begin{pmatrix} \frac{3}{2}t_1 \\ -2-\frac{1}{2}t_1+t_2 \\ t_1-t_2 \end{pmatrix} $$
Devo trovare il valore del parametro t che rende ortogonale il segmento H1H2 con entrambi i vettori direttori delle rette
Per essere ortogonale deve essere nullo sia il prodotto scalare <H1H2,v1> e sia <H1H2,v2>
$$ \begin{cases} < v_{r1} , \overrightarrow{H_{r1}H_{r2}} > = 0 \\ < v_{r2} , \overrightarrow{H_{r1}H_{r2}} > = 0 \end{cases} $$
$$ \begin{cases} < \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix} , \begin{pmatrix} \frac{3}{2}t_1 \\ -2-\frac{1}{2}t_1+t_2 \\ t_1-t_2 \end{pmatrix} > = 0 \\ < \begin{pmatrix} \frac{3}{2} \\ -\frac{1}{2} \\ 1 \end{pmatrix} , \begin{pmatrix} \frac{3}{2}t_1 \\ -2-\frac{1}{2}t_1+t_2 \\ t_1-t_2 \end{pmatrix} > = 0 \end{cases} $$
$$ \begin{cases} (2 + \frac{1}{2} t_1-t_2) + (t_1-t_2) =0\\ ( \frac{9}{4}t_1 ) + (1 + \frac{1}{4}t_1 - \frac{1}{2} t_2 ) + (t_1-t_2)=0 \end{cases} $$
$$ \begin{cases} 2 + \frac{3}{2} t_1-2t_2 =0\\ \frac{7}{2}t_1 - \frac{3}{2} t_2 + 1 =0 \end{cases} $$
$$ \begin{cases} t_1 = \frac{4}{19} \\ t_2 = \frac{22}{19} \end{cases} $$
Una volta trovati i parametri che rendono ortogonale il segmento H1H2, li sostituisco nei punti mobili delle rette per trovare le coordinate dei punti di incidenza H1.
$$ H_{r1} = \begin{pmatrix} 0 \\ 1-t_1 \\ t_1 \end{pmatrix} = \begin{pmatrix} 0 \\ \frac{15}{19} \\ \frac{4}{19} \end{pmatrix} $$
Sapendo che il vettore H1H2 è
$$ \overrightarrow{H_{r1}H_{r2}} = \begin{pmatrix} \frac{3}{2}t_1 \\ -2-\frac{1}{2}t_1+t_2 \\ t_1-t_2 \end{pmatrix} $$
$$ \overrightarrow{H_{r1}H_{r2}} = \begin{pmatrix}\frac{3}{2} \cdot \frac{4}{19} \\ -2-\frac{1}{2} \cdot \frac{4}{19} + \frac{22}{19} \\ \frac{4}{19}- \frac{22}{19} \end{pmatrix} $$
$$ \overrightarrow{H_{r1}H_{r2}} = \begin{pmatrix} \frac{6}{19} \\ - \frac{18}{19} \\ -\frac{18}{19} \end{pmatrix} $$
Per conoscere la distanza tra i due punti devo soltanto calcolare la norma del vettore H1H2.
$$ \sqrt{(\frac{6}{19})^2+(-\frac{18}{19})^2+(-\frac{18}{19})^2} = 1,37 $$
Ho così trovato la distanza minima tra le due rette.
E così via.
