Gli angoli
Un angolo è la parte di un piano compresa tra due semirette che hanno origine da uno stesso punto.
Le due semirette sono dette lati dell'angolo.
Il punto di origine è invece detto vertice dell'angolo.

L'ampiezza dell'angolo tra le due semirette si può misurare in gradi usando il sistema sessagesimale (gradi) oppure il sistema in radianti.
Per indicare l'ampiezza dell'angolo posso usare una lettera minuscola dell'alfabeto greco ( es. α, β, γ, ecc. ).
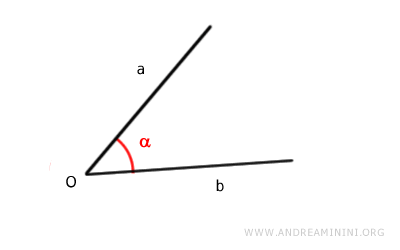
In alternativa, posso usare la notazione aÔb dove "a" e "b" sono i nomi dei lati mentre "Ô" è il nome del vertice dell'angolo.
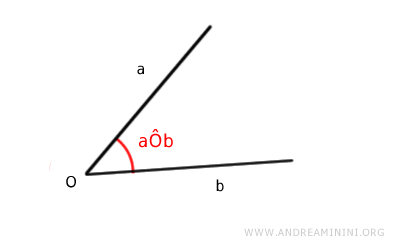
Tutti i punti compresi tra i due lati dell'angolo che non appartengono alle semirette sono detti punti interni dell'angolo.
Gli altri punti sono detti punti esterni dell'angolo.
La misura dell'angolo
Per misurare l'ampiezza dell'angolo si associa a ogni ampiezza una grandezza numerica secondo un sistema di misurazione.
I principali sistemi di misurazione degli angoli sono i gradi (sistema sessagesimale) e i radianti.
- La misura in gradi
Consiste nel dividere una circonferenza (angolo giro) in 360 parti uguali dette gradi. - La misura in radianti
Un radiante è un angolo che delinea un arco sulla circonferenza di uguale lunghezza rispetto al raggio. In un angolo giro ci sono 2π radianti (rad) ossia circa 6,28 radianti.
L'ampiezza degli angoli consente di classificare tutti gli angoli del piano in insiemi/classi di angoli congruenti tra loro.
Ogni classe individua una sola ampiezza.
In particolar modo, due o più angoli sono detti angoli congruenti se hanno la stessa ampiezza.
Pertanto, due angoli congruente appartengono alla stessa classe di equivalenza.
Nota. Non occorre che gli angoli congruenti condividano gli stessi punti del piano o che abbiano lo stesso orientamento nello spazio. Ciò che conta per soddisfare la relazione di congruenza è che abbiano la stessa ampiezza.
Per confrontare due angoli bisogna sovrapporre il primo angolo al secondo angolo con un movimento rigido, facendo in modo che un lato di entrambi gli angoli coincida e che gli angoli si trovano dalla stessa parte rispetto al lato comune.
Se i due angoli si sovrappongono perfettamente, allora sono congruenti $ \alpha \cong \beta $. Viceversa, sono angoli di diversa ampiezza.
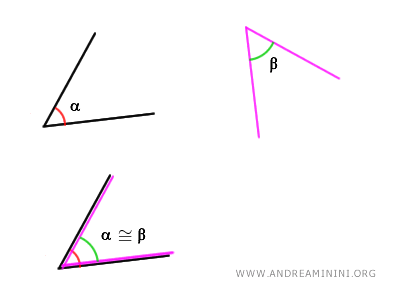
Non importa se i lati dell'angolo sono lunghi o corti, perché l'ampiezza degli angoli non dipende dalla lunghezza dei lati.
Tipi di angoli
Esistono diversi tipi di angoli.
- Angoli concavi
Un angolo è detto concavo se contiene i prolungamenti dei suoi lati.
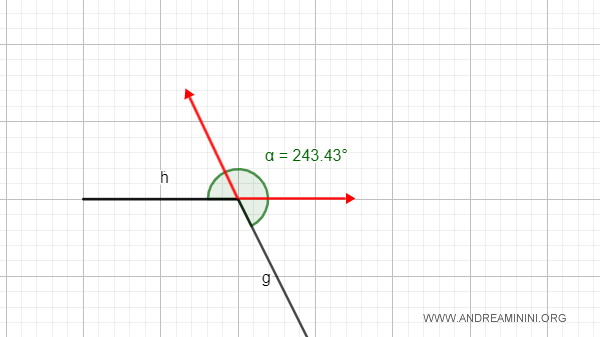
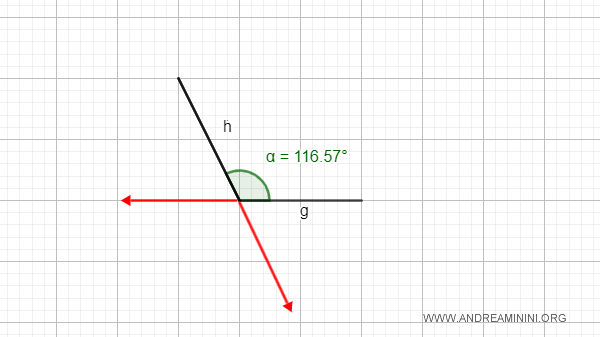
- Angoli convessi
Un angolo è detto convesso se non contiene i prolungamenti dei suoi lati.
- Angolo retto
Un angolo è detto retto se le rette sono perpendicolari tra loro, ossia formano quattro angoli congruenti. Un angolo retto ha un'ampiezza di 90° (π/2 radianti).
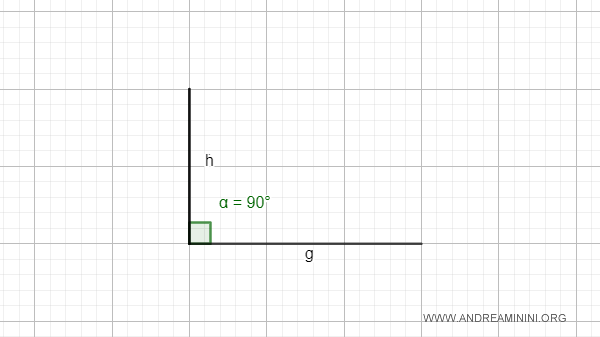
Nota. Due angoli sono detti angoli congruenti quando hanno la stessa ampiezza.
- Angolo giro
Un angolo è detto angolo giro se i lati coincidono tra loro e l'angolo contiene tutti i punti del piano. Ha un'ampiezza di 360° (2π radianti)
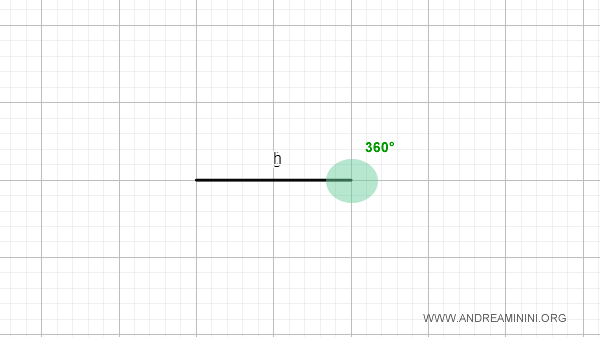
Nota. In un angolo giro i lati sono semirette coincidenti.
- Angolo nullo
Un angolo è detto angolo nullo se i lati sono coincidenti e l'angolo contiene soltanto i punti delle semirette dei lati. Ha un'ampiezza di 0° (zero π radianti)
Gli angoli orientati
Per convenzione un angolo è positivo quando la rotazione avviene in senso antiorario.
Il lato di origine associato all'angolo zero è il semiasse positivo delle ascisse.
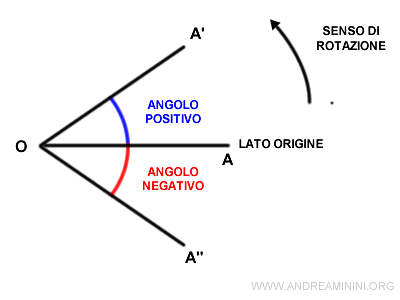
Viceversa se la rotazione avviene in senso orario l'angolo ha segno negativo.
E' una convenzione adottata in quasi tutti i testi di matematica e fisica.
Gli angoli adiacenti e consecutivi
Gli angoli consecutivi e adiacenti sono due tipi di angoli che si differenziano per la loro posizione rispetto ad una linea o ad un punto.
- Gli angoli consecutivi
Due angoli sono consecutivi se hanno il vertice e un lato in comune.
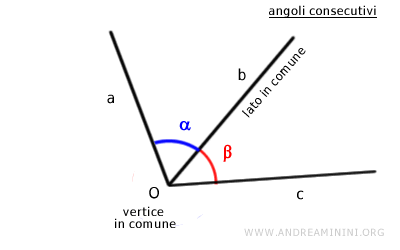
- Gli angoli adiacenti
Due angoli sono adiacenti se hanno il vertice e un lato in comune e gli altri lati non in comune appartengono alla stessa retta.
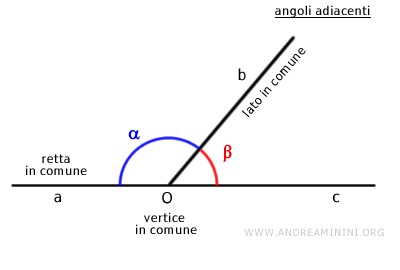
Nota. Gli angoli adiacenti sono anche angoli consecutivi ma non è detto il contrario. La somma di due angoli adiacenti è sempre 180° ossia un angolo piatto.
Angoli concavi e convessi
Gli angoli possono essere sia figure concave che figure convesse.
- Angoli concavi
Un angolo è definito come concavo quando include i prolungamenti dei suoi lati, ad eccezione dell'angolo giro.
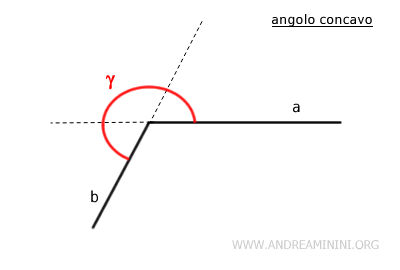
Posso identificare un angolo concavo anche scegliendo due punti interni dell'angolo P e Q e tracciando un segmento tra questi due punti. Se questo segmento non è completamente contenuto all'interno dell'angolo, ossia include dei punti esterni, allora l'angolo è concavo.
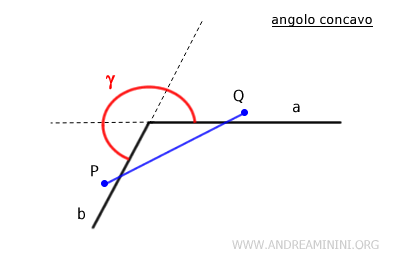
Nota. L'angolo giro (360 gradi) non è considerato un angolo concavo, perché presi due punti interni qualsiasi, il segmento che li unisce è interamente compreso nell'angolo. Non ha punti esterni.
- Angoli convessi
Un angolo è definito come convesso quando non include i prolungamenti dei suoi lati.
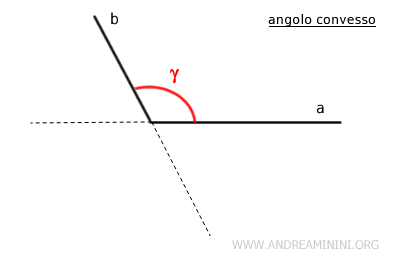
In questo caso, se prendo due punti qualsiasi P e Q all'interno di questo angolo e li connetto con un segmento, questo segmento resta completamente all'interno dell'angolo. In altre parole, il segmento non ha punti esterni dell'angolo.
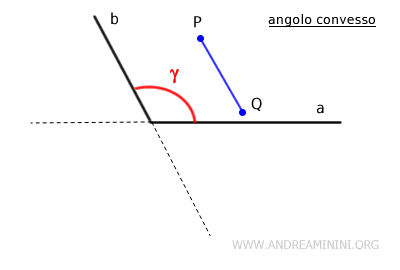
Quindi, tutti gli angoli da 0 a 180° sono angoli convessi.
Nota. L'angolo piatto (180°) è considerato un angolo convesso, perché i punti sui lati dell'angolo piatto non sono punti interni dell'angolo. Pertanto, se prendo due punti interni qualsiasi, questi non intersecano mai né i lati, né i loro prolungamenti.
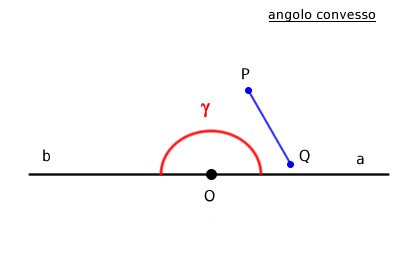
E così via
