L'equazione della retta in forma polare

L'equazione della retta in forma polare


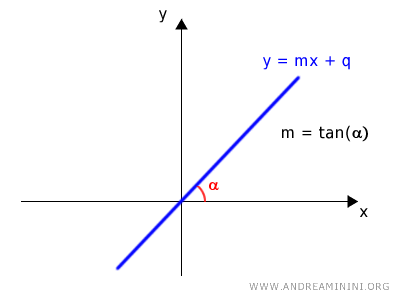
• Se la retta passa per l'origine è sufficiente conoscere l'angolo α che determina il coefficiente angolare (m) della retta y=mx+q $$ m = \tan \alpha \ \ \ \ con \ \alpha \ne \frac{\pi}{2}+k \pi $$ Dove q=0.
  
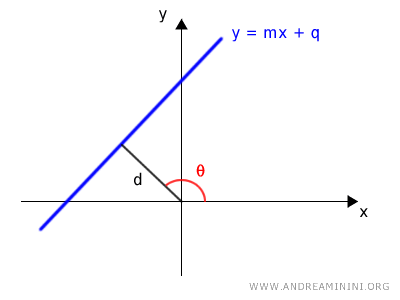
• Se la retta non passa per l'origine occorre conoscere la distanza d tra la retta e il polo (origine) e l'angolo β del segmento della distanza rispetto al semiasse polare positivo $$ d = r \cdot \cos ( \beta - \alpha) $$
  

  
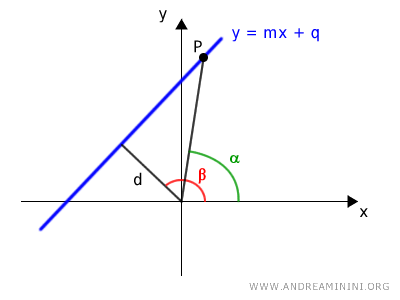
  Dove α è l'angolo delle coordinate polari di un altro punto P generico della retta
  
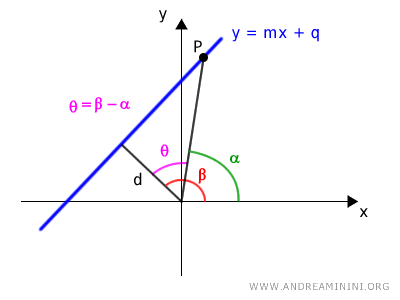
  La differenza θ=β-α è l'angolo interno tra i due segmenti
  

Ovviamente se la retta passa per l'origine la distanza d=0 è nulla.

Un esempio pratico

Esempio 1: dalla forma cartesiana alla forma polare

Considero la retta

$$ y = 2x + 3 $$

Devo ottenere le coordinate polari della retta.

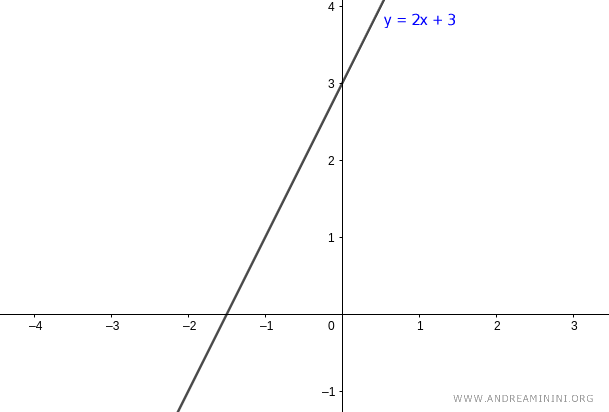
Il coefficiente angolare della retta è m=2

$$ m = 2 $$

Quindi l'angolo tra la retta l'asse polare è

$$ m = \tan \alpha $$

Calcolo l'arcotangente a entrambi i membri

$$ \arctan(m) = \arctan(\tan \alpha) $$

$$ \arctan(m) = \alpha $$

Sapendo che m = 2

$$ \alpha = \arctan(2) $$

$$ \alpha = 63.43° $$

Pertanto l'angolo tra la retta e l'asse polare è α=63.43°

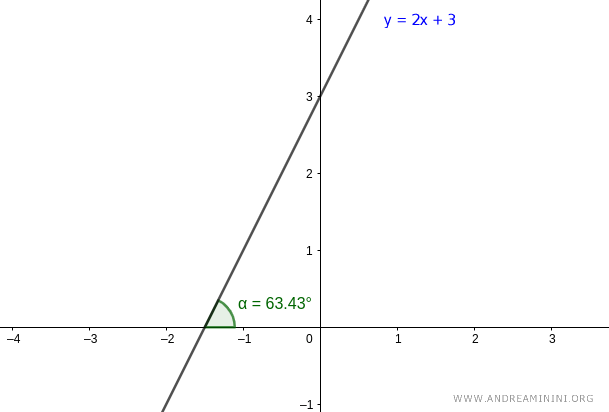
Ho così ottenuto uno dei parametri delle coordinate polari della retta.

A questo punto devo calcolare l'altro parametro ossia la distanza (d) tra la retta e il polo (origine).

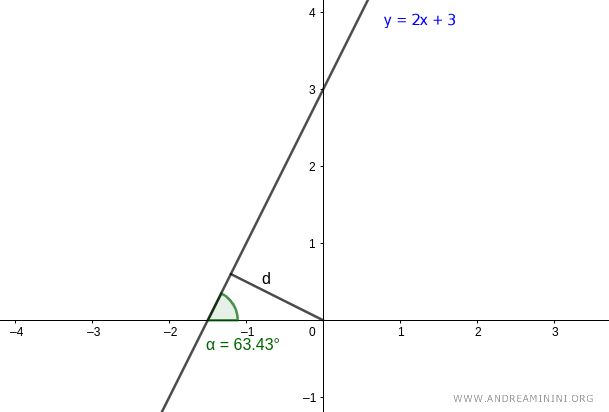
Prendo un altro punto P qualsiasi della retta.

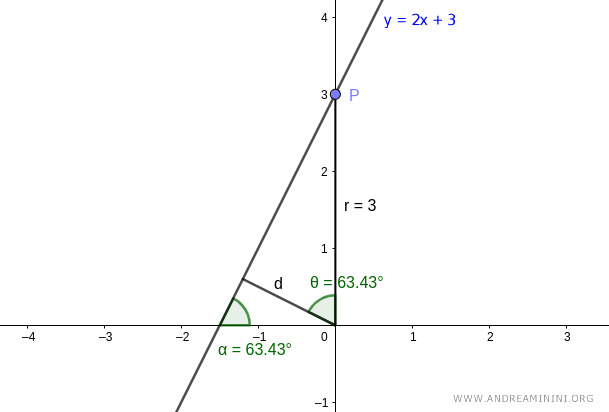
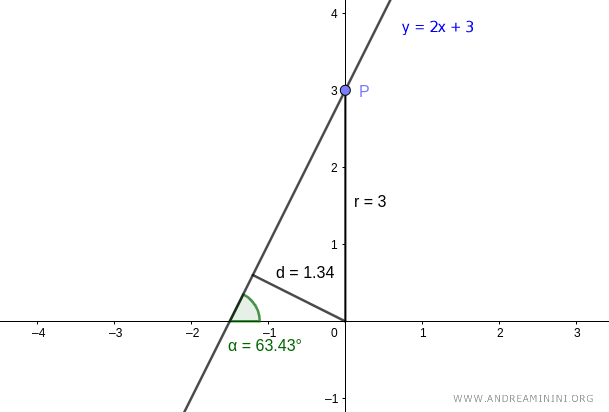
Per semplicità considero il punto P alle coordinate (0,3) di lunghezza r=3, in questo modo l'angolo θ tra i due segmenti coincide con l'angolo α = θ = 63.43°

Nota. Qualsiasi altro punto P della retta sarebbe comunque andato bene.

Una volta noti l'angolo θ=63.43° e la lunghezza r=3 posso calcolare la distanza (d)

$$ d = r \cdot \cos ( θ ) $$

$$ d = 3 \cdot \cos ( 63.43° ) $$

$$ d = 1.34 $$

Ho ottenuto anche la distanza minima (d) tra la retta e il polo.

Quindi le coordinate polari della retta sono [63.43°, 1.34]

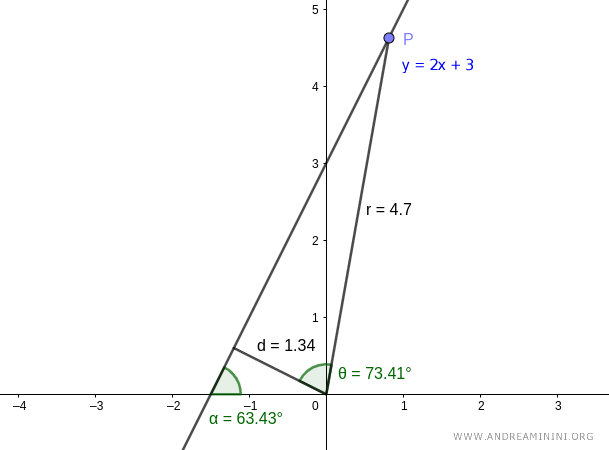
Nota. Come già anticipato, qualsiasi altro punto P della retta sarebbe andato bene. Ad esempio, scegliendo un altro punto P della retta con coordinate diverse ho un angolo interno diverso θ=73.41° e una lunghezza r=4.7 ma ottengo comunque la stessa distanza d=4.7·cos(73.41°)=1.34.

Esempio 2: dalla forma polare alla forma cartesiana

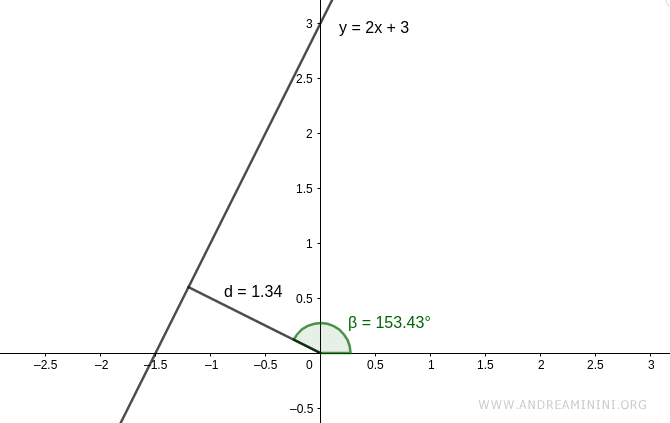
Considero una retta in forma polare

$$ d = 1.34 $$

$$ \beta = 153.43 $$

Da questi dati devo ricavare l'equazione in forma cartesiana y=mx+q

Considero le coordinate polari [α,r] un generico altro punto P della retta.

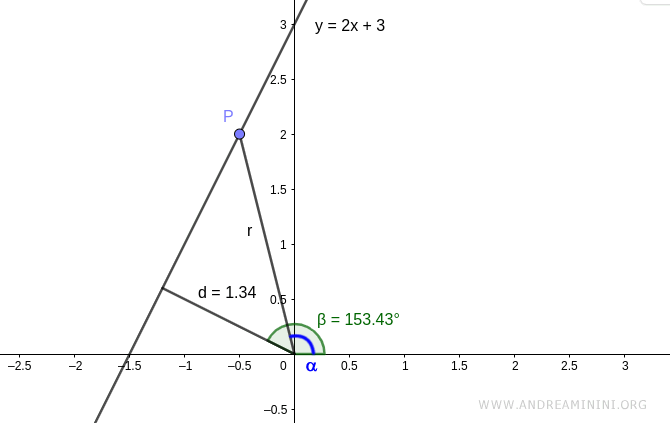
Sapendo che la distanza (d) della retta dal polo (origine) si ottiene con la formula

$$ d = r \cdot \cos (θ) $$

Dove θ è l'angolo interno tra i due segmenti d e r che si ottiene anche per differenza tra i due angoli θ=β-α

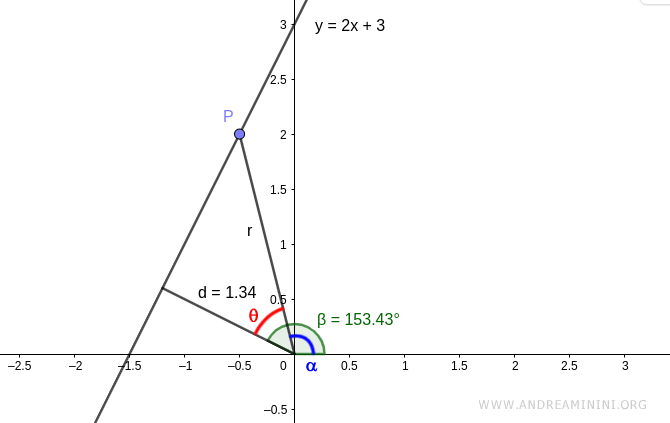
Sapendo che θ=β-α la formula della distanza posso scriverla in questa forma

$$ d = r \cdot \cos (\beta - \alpha) $$

Conosco l'angolo beta β=153.43°

$$ d = r \cdot \cos (153.43° - \alpha) $$

Conosco anche la distanza d=1.34

$$ 1.34 = r \cdot \cos (153.43° - \alpha) $$

Applico la formula della sottrazione del coseno ossia cos(β-α)=cos(β)cos(α)+sin(β)sin(α)

$$ 1.34 = r \cdot [ \cos (153.43°) \cos (\alpha) + \sin(153.43°) \sin(\alpha) ] $$

$$ 1.34 = r \cdot \cos (153.43°) \cos (\alpha) + r \cdot \sin(153.43°) \sin(\alpha) $$

Sapendo che x=r·cos(α)

$$ 1.34 = [ r \cdot \cos (\alpha) ] \cos (153.43°) + r \cdot \sin(153.43°) \sin(\alpha) $$

$$ 1.34 = x \cdot \cos (153.43°) + r \cdot \sin(153.43°) \sin(\alpha) $$

Sapendo che y=r·sin(α)

$$ 1.34 = x \cdot \cos (153.43°) + [ r \cdot \sin(\alpha) ] \sin(153.43°) $$

$$ 1.34 = x \cdot \cos (153.43°) + y \cdot \sin(153.43°) $$

Esplicito la variabile y

$$ y = \frac{ 1.34 } { \sin(153.43°) } - x \cdot \frac{ \cos (153.43°) }{ \sin(153.43°) } $$

Il rapporto cos(153.43°)/sin(153.43°) è uguale a -2

$$ y = \frac{ 1.34 } { \sin(153.43°) } - x \cdot (-2) $$

$$ y = \frac{ 1.34 } { \sin(153.43°) } + 2x $$

Il rapporto 1.34/sin(153.43°) è uguale a 3

$$ y = 3 + 2x $$

In questo modo ottengo l'equazione cartesiana della retta.

La dimostrazione

1) La retta passante per l'origine

Nell'equazione della retta passante per l'origine si ha q=0

$$ y=m \cdot x $$

Dal punto di vista grafico

Prendo un punto P qualsiasi della retta.

Il punto P ha le coordinate cartesiane (x,y)

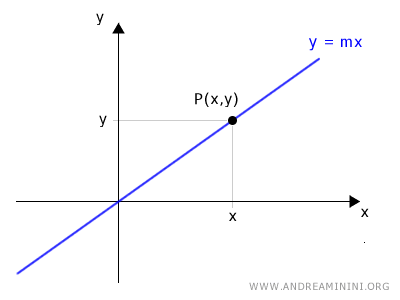
Traccio un segmento tra l'origine O e il punto P.

Il segmento OP ha una lunghezza r e un angolo orientato di α gradi rispetto all'asse dell'ascissa.

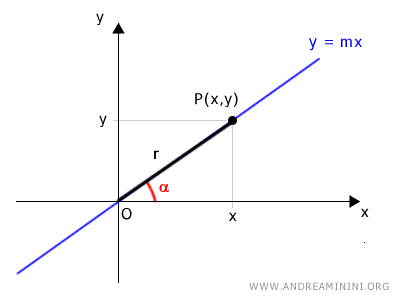
Conoscendo l'angolo α e la lunghezza del segmento OP, le coordinate cartesiane (x,y) del punto P posso scriverle in forma trigonometrica tramite le funzioni seno e coseno.

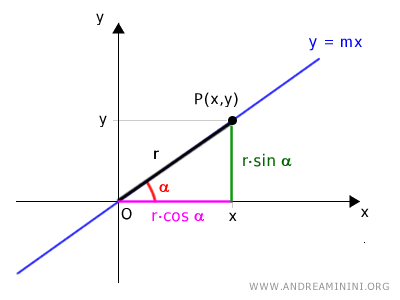
Quindi le coordinate polari del punto P sono [r,α]

$$ y = r \cdot \sin \alpha $$ $$ x = r \cdot \cos \alpha $$

Sostituisco x e y in forma trigonometrica nell'equazione della retta

$$ y=m \cdot x $$

$$ r \cdot \sin \alpha =m \cdot (r \cdot \cos \alpha) $$

Semplifico eliminando la variabile r dal membro di destra e di sinistra

$$ \sin \alpha =m \cdot \cos \alpha $$

Determino il coefficiente angolare m della retta

$$ m = \frac{\sin \alpha}{\cos \alpha} $$

In base al secondo principio della trigonometria tan α=sin α/cos α

Quindi, sostituisco il rapporto tra seno e coseno con la tangente.

$$ m = \tan \alpha $$

La tangente non è definita nell'angolo retto 90° (π/2) e nei suoi multipli 90°±k·180° ossia π/2±k·π

$$ m = \tan \alpha \ \ \ \ con \ \alpha \ne \frac{\pi}{2}+k \pi $$

Dove k è un numero intero qualsiasi.

In questo modo ho dimostrato la formula dell'equazione polare della retta passante per l'origine.

2) Equazione della retta non passante per l'origine

Traccio una retta passante per un punto P del piano ma non per l'origine

Qualsiasi retta che non passa per l'origine può essere individuata in modo univoco tramite due parametri polari

• la distanza (d) tra la retta e il polo
• l'angolo β tra la retta della distanza e l'asse polare

La distanza (minima) tra la retta e il polo è un segmento OA passante per l'origine (polo) e perpendicolare alla retta.

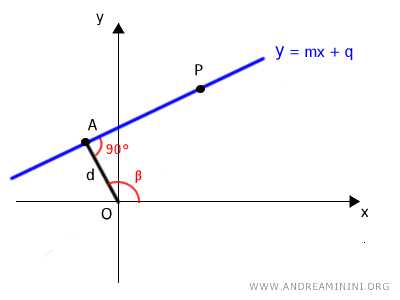
Il segmento OA ha un angolo di β gradi rispetto all'asse polare e una lunghezza d che ancora non conosco.

Per calcolare la distanza (d) traccio un segmento OP tra il polo e il punto P della retta.

Il segmento OP ha un angolo orientato α rispetto all'asse polare.

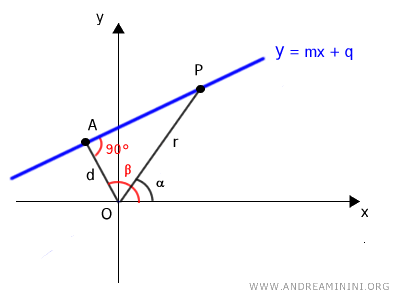
In questo modo ottengo un triangolo rettangolo OAP

Questo mi permette di usare i teoremi del triangolo rettangolo.

In base al primo teorema dei triangoli rettangoli la lunghezza di un cateto (OA) è uguale al prodotto tra l'ipotenusa (OP) per il coseno dell'angolo acuto adiacente θ=AOP

$$ \overline{OA} = \overline{OP} \cdot \cos \widehat{AOP} $$

Dove l'angolo θ=AOP è l'angolo acuto adiacente al cateto OA

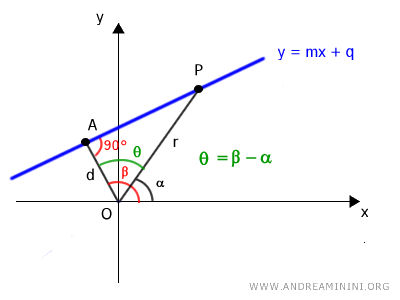
L'angolo θ=OAP posso scriverlo anche come differenza tra gli angoli beta e alfa θ=β-α

$$ \overline{OA} = \overline{OP} \cdot \cos (\beta - \alpha) $$

Sapendo che OA è la distanza (d) tra la retta e il polo mentre OP è la lunghezza (r)

$$ d = r \cdot \cos (\beta - \alpha) $$

Ho ottenuto la formula della distanza che volevo dimostrare.

E così via.