Coniche

Le coniche (o sezioni coniche) sono una famiglia di curve nel piano ottenute dall'intersezione tra un cono circolare retto e un piano.

A seconda dell'inclinazione e della posizione del piano rispetto al cono, si ottengono diversi tipi curve: ellisse, parabola e iperbole.

In generale una conica è un luogo di punti nel piano che soddisfano la sequente equazione di secondo grado:

$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$

Dove almeno uno tra i coefficienti A, B e C è diverso da zero.

Calcolando il discriminante dell'equazione si può capire se ammette soluzioni oppure no.

$$ \Delta = B^2 - 4AC $$

• Se $ \Delta <0 $ l'equazione rappresenta un'ellisse o una circonferenza
• Se $ \Delta =0 $ l'equazione rappresenta una parabola
• Se $ \Delta >0 $ l'equazione rappresenta un'iperbole

In generale, va detto che questo criterio funziona bene solo per distinguere il tipo geometrico principale (ellittica, parabolica, iperbolica). Tuttavia, non basta per garantire che ci siano soluzioni reali non vuote, ossia che la curva sia disegnabile e non sia solo immaginaria, né per escludere le degenerazioni.

Gli antichi greci furono i primi ad accorgersi che alcune curve erano ottenibili tramite delle sezioni coniche. In particolar modo, le sezioni coniche furono analizzate in dettaglio durante l'epoca ellenistica, intorno al 200 a.C., da Menecmo e Apollonio di Perga. Fu Apollonio a denominare le tre principali coniche come ellisse, parabola e iperbole, considerando la circonferenza un caso particolare dell'ellisse. Inizialmente, i greci utilizzavano uno cono diverso tagliato da un piano inclinato per ottenere la parabola, l'ellisse e l'iperbole. Apollonio dimostrò che si potevano ottenere anche usando lo stesso cono (retto o obliquo) inclindando semplicemente il piano di intersezione.

Le caratteristiche di una sezione conica

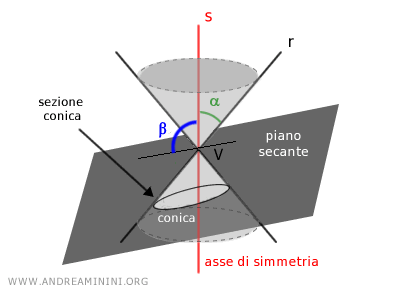
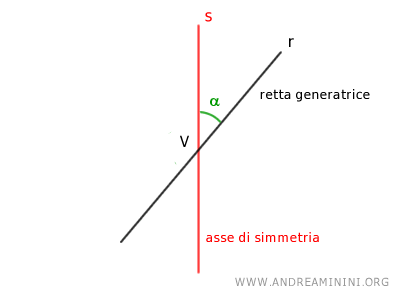
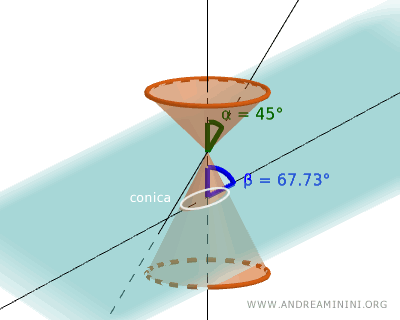
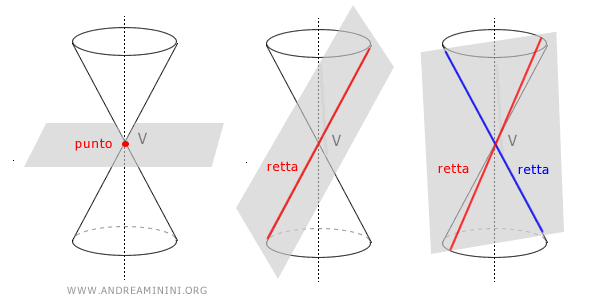
Per ottenere una conica faccio intersecare due rette r e s con un angolo α (detto semiapertura) in un punto V dello spazio detto "vertice".

La rotazione completa della retta r intorno alla retta s genera una superficie conica a due falde.

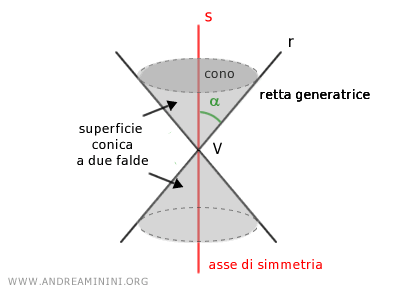
Per questa ragione la retta r è detta retta generatrice mentre la retta s è detta asse di rotazione.

Lo spazio all'interno della superficie è, invece, detto cono a due falde.

A questo punto interseco la conica a due falde con un piano con una determinata inclinazione β rispetto all'asse di simmetria.

I punti di intersezione del piano secante con la conica a due falde generano una curva detta "sezione conica" o semplicemente "conica"

Ad esempio, la conica della figura precedente mi appare sul piano in questa forma

A seconda dell'angolo α del cono (semiapertura) e dell'angolo β del piano posso ottenere diverse curve aperte o chiuse.

• Se β<α la sezione conica è una iperbole, ossia una curva aperta composta da due rami illimitati, perché il piano interseca due falde del cono.
  
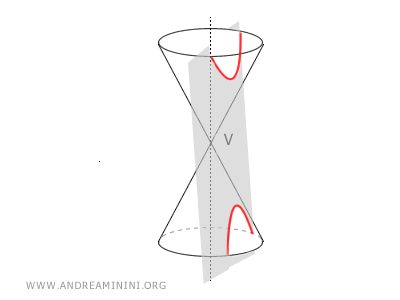
• Se β=α la sezione conica è una parabola, ossia una curva aperta e illimitata composta da un solo ramo, perché il piano ha la stessa inclinazione dell'angolo del cono e interseca una sola falda del cono.
  
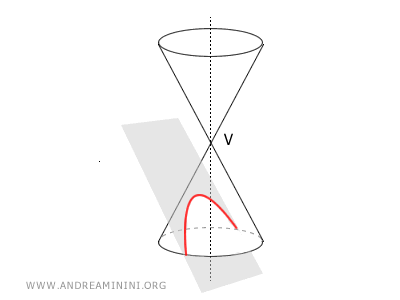
• Se β>α la sezione conica è una ellisse, ossia una curva chiusa e limitata, perché l'angolo del piano è maggiore della semiapertura.
  

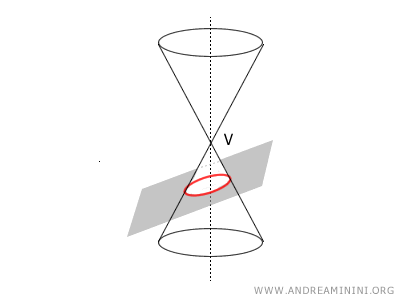
  Esempio
  

• Se β=π/2 è un angolo retto (90°), dove "π" rappresenta il numero pi greco, la sezione conica si riduce a una circonferenza, ossia una curva chiusa e limitata con tutti i punti equidistanti dal suo centro.
  

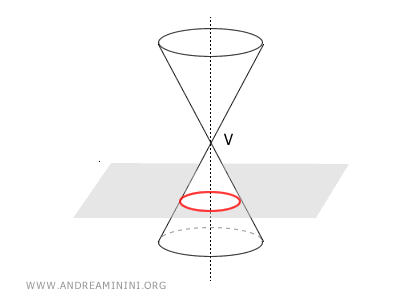
Tipi di coniche

Le coniche sono classificate in base alla loro forma e alle proprietà geometriche:

• Ellisse
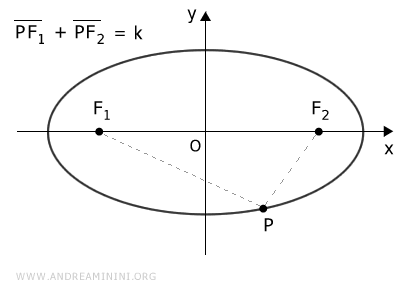
  L'ellisse è una curva chiusa ottenuta intersecando un cono con un piano inclinato tra θ e π/2 rispetto al suo asse. È definita dalla somma costante delle distanze dai suoi due fuochi. Ha due assi di simmetria, maggiore e minore. Se i due assi sono uguali si ottiene un cerchio.
  
• Parabola
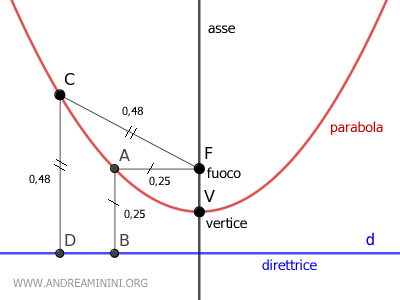
  La parabola è l'insieme dei punti equidistanti da un fuoco (F) e una retta direttrice (d). Ha un asse di simmetria e si forma intersecando un cono con un piano parallelo a una sua retta generatrice, formando un angolo θ con l'asse della conica. Non è una curva chiusa e appartiene a una sola falda del cono.
  
• Iperbole
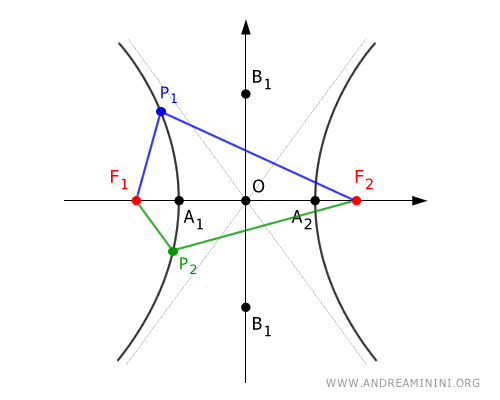
  L'iperbole è formata dall'intersezione di un cono con un piano inclinato meno di θ rispetto all'asse del cono. È definita dai punti la cui differenza di distanza da due fuochi fissi è costante. E' curva aperta e, poiché interseca entrambe le falde del cono, si divide in due rami opposti con due assi di simmetria.
  
• Circonferenza
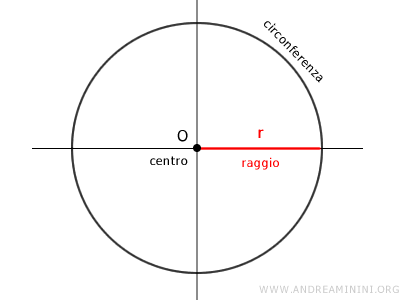
  La circonferenza è un caso particolare di ellisse che si ottiene facendo intersecare il cono retto con un piano perpendicolare al suo asse. E' una curva chiusa.
  

Nota. Questi tipi di coniche sono dette "non degeneri" per distinguerle dalle coniche "degeneri" come il punto, la retta e una coppia di rette. Ad esempio, il punto può essere considerato una conica degenere che si ottiene intersecando la conica con un piano passante per il vertice del cono. Lo stesso vale per il piano che interseca una retta o due rette della conica. Anche in questi casi si parla di "coniche degeneri".

La definizione di conica

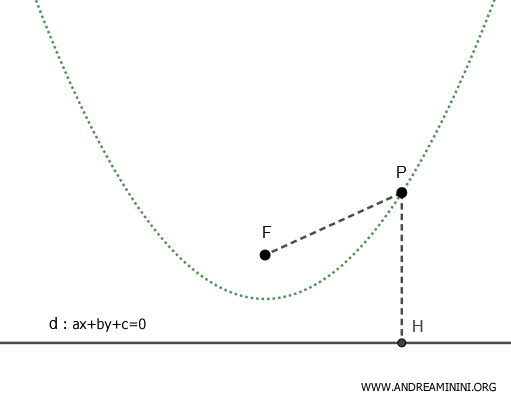
Ogni punto $ P(x;y) $ di una conica ha un rapporto costante $$ \frac{ \overline{PF} }{ \overline{PH} } = e $$ Dove PF è la distanza tra il punto P e un punto fisso $ F(p;q) $ detto "fuoco" mentre PH è la distanza tra il punto P e una retta fissa d: $ ax+by+c=0 $ detta "direttrice" che non passa per P. 

Il rapporto costante "e" è un numero reale costante, non negativo, che determina l'eccentricità della conica.

L'eccentricità della conica determina il tipo di conica

• Se e=0 la conica è una circonferenza
• Se 0<e<1 la conica è un'ellisse
• Se e=1 la conica è una parabola
• Se e>1 la conica è un'iperbole

Nota. La parabola ha un fuoco e una retta direttrice. L'ellisse e l'iperbole, invece, hanno due fuochi e due rette direttrici simmetriche rispetto al centro di simmetria e perpendicolari all'asse focale. Infine, la circonferenza si può interpretare come una conica con una retta direttrice posta a una distanza infinita dal centro. La circonferenza, tecnicamente, non ha una sola retta direttrice ma infinite tutte poste a distanza infinita dal centro.

Esempio

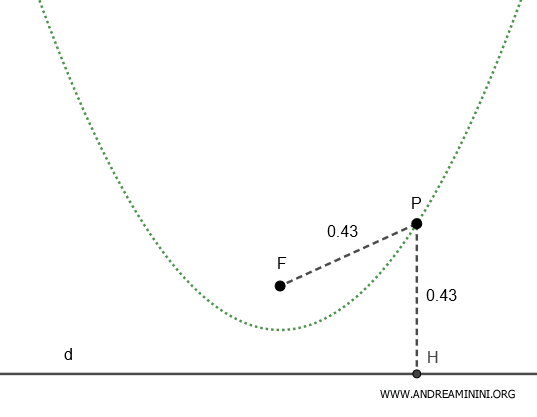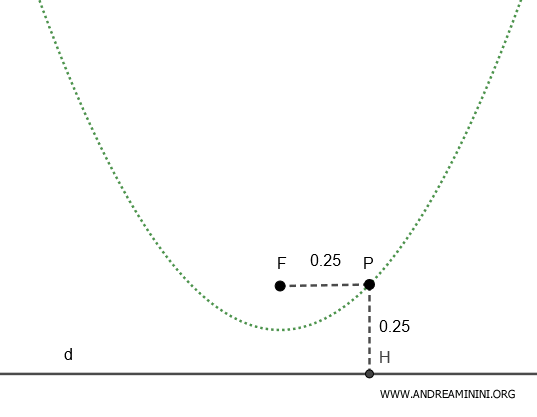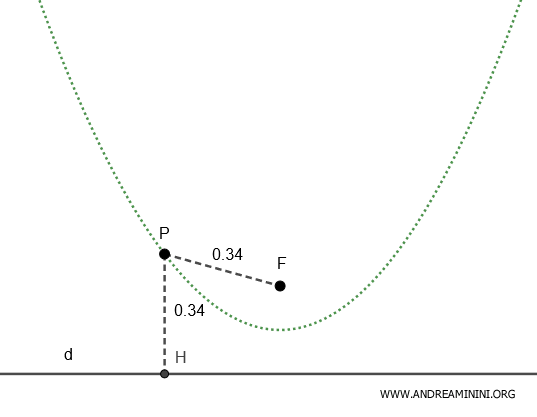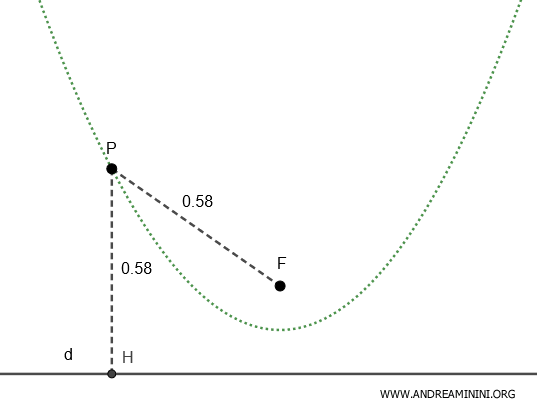
In una parabola l'eccentricità è $ e=1 $ uguale a uno.

$$ e = 1 $$

Quindi la distanza PF tra un punto P della parabola e il fuoco F è uguale alla distanza PH tra lo stesso punto P e la retta direttrice d.

$$ \frac{ \overline{PF} }{ \overline{PH} } = e = 1 $$

$$ \overline{PF} =  \overline{PH} $$

In questo caso il rapporto tra le due distanze $ \frac{ \overline{PF} }{ \overline{PH} } = 1 $ è sempre uguale a uno.

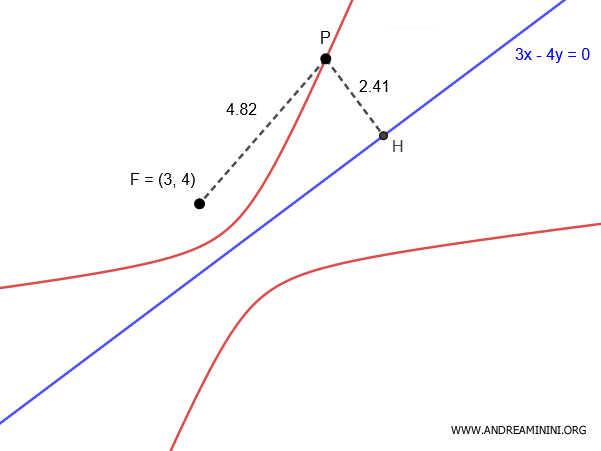
Esempio 2

Considero un fuoco alle coordinate $ F(3;4) $ e una retta $ 3x-4y=0 $

Devo determinare il luogo geometrico dei punti del piano $ P(x;y) $ in cui l'eccentricità è uguale a $ e = 2 $

$$ e = 2 $$

L'eccentricità di una conica è uguale al rapportro tra le distanze PF e PH ed è costante.

$$ \frac{ \overline{PF} }{ \overline{PH} } = 2 $$

$$ \overline{PF} = \overline{PH} \cdot 2 $$

La distanza euclidea tra i punti $ P(x;y) $ e $ F(p;q)=(3;4) $ è la seguente:

$$ \overline{PF} = \sqrt{(x-p)^2+(y-q)^2} $$

$$ \overline{PF} = \sqrt{(x-3)^2+(y-4)^2} $$

La distanza tra i punti $ P(x;y) $ e la retta direttrice $ 3x-4y=0 $ è la seguente:

$$ \overline{PH} = \frac{|3x-4y|}{ \sqrt{3^2+(-4)^2} } $$

$$ \overline{PH} = \frac{|3x-4y|}{ \sqrt{9+16} } $$

$$ \overline{PH} = \frac{|3x-4y|}{ \sqrt{25} } $$

$$ \overline{PH} = \frac{|3x-4y|}{ 5 } $$

Sostituisco le distanze nella formula dell'eccentricità

$$ \overline{PF} = \overline{PH} \cdot 2 $$

$$ \sqrt{(x-3)^2+(y-4)^2} = \frac{|3x-4y|}{ 5 } \cdot 2 $$

Elevo entrambi i lati dell'equazione al quadrato

$$ ( \sqrt{(x-3)^2+(y-4)^2} )^2 = ( \frac{|3x-4y|}{ 5 } \cdot 2 )^2 $$

$$ (x-3)^2+(y-4)^2 = \frac{(|3x-4y|)^2}{ 5^2 } \cdot 2^2 $$

$$ (x-3)^2+(y-4)^2 = \frac{(3x-4y)^2}{ 25 } \cdot 4 $$

Espando i quadrati

$$ (x^2-6x+9) + (y^2-8y+16) = \frac{ (9x^2-24xy+16y^2)}{ 25 } \cdot 4 $$

$$  x^2 - 6x + 9 + y^2 - 8y + 16 = \frac{36x^2 - 96xy + 64y^2}{25} $$

$$ 25(x^2 - 6x + y^2 - 8y + 25) = 36x^2 - 96xy + 64y^2  $$

$$ 25x^2 - 150x  + 25y^2 - 200y + 625 - 36x^2 + 96xy - 64y^2 = 0 $$

$$ (25 - 36)x^2 + 96xy + (25 - 64)y^2 - 150x - 200y + 625 = 0 $$

Quindi, l'equazione generale della conica è:

$$  -11x^2 + 96xy - 39y^2 - 150x - 200y + 625 = 0 $$

Questa conica è caratterizzata da un rapporto costante $ \frac{ \overline{PF} }{ \overline{PH} } = 2 $.

Equazione generale di una conica

Ogni conica è descritta da un'equazione di secondo grado del tipo $$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$ con i coefficienti A, B, C, D, E, F non tutti contemporaneamente nulli.

Ad esempio, se B=0 e A=0 l'equazione rappresenta una parabola con l'asse parallelo all'asse x.

$$ Cy^2 + Dx + Ey + F = 0 $$

Se invece fisso B=0 e C=0, l'equazione rappresenta una parabola con l'asse parallelo all'asse y.

$$ Ax^2 + Dx + Ey + F = 0 $$

Se B=0 e A=C con A≠0, l'equazione della conica rappresenta una circonferenza.

$$ Ax^2 + Cy^2 + Dx + Ey + F = 0 $$

Se B=0 e A≠C con A≠0 e C≠0, l'equazione della conica rappresenta una ellisse se A e C sono concordi (A·C>0) oppure un'iperbole se A e C sono discordi (A·C<0).

$$ Ax^2 + Cy^2 + Dx + Ey + F = 0 $$

Spiegazione. Raccolgo le variabili x e y $$ Ax^2 + Cy^2 + Dx + Ey + F = 0 $$ $$ A ( x^2  + \frac{Dx}{A} ) + C (y^2 + \frac{Ey}{A} ) + F = 0 $$ Poi completo i quadrati $$ A ( x^2  + \frac{Dx}{A} + ( \frac{D}{2A})^2 - ( \frac{D}{2A})^2 ) + C (y^2 + \frac{Ey}{C}  + (  \frac{E}{2C}  )^2 -  ( \frac{E}{2C}  )^2 ) + F = 0 $$ $$ A ( x^2  + \frac{Dx}{A} +  \frac{D^2}{4A^2} - \frac{D^2}{4A^2} ) + C (y^2 + \frac{Ey}{C}  +  \frac{E^2}{4C^2}  -  \frac{E^2}{4C^2}   ) + F = 0 $$ $$ A ( x^2  + \frac{Dx}{A} +  \frac{D^2}{4A^2}  ) + C (y^2 + \frac{Ey}{C}  +  \frac{E^2}{4C^2}    ) + F - \frac{D^2}{4A} -  \frac{E^2}{4C} = 0 $$ $$ A ( x +  \frac{D}{2A} )^2  + C (y +  \frac{E}{2C}    )^2 + F - \frac{D^2}{4A} -  \frac{E^2}{4C} = 0 $$$$ A ( x +  \frac{D}{2A} )^2  + C (y +  \frac{E}{2C}    )^2 = \frac{D^2}{4A} +  \frac{E^2}{4C} - F $$ Considero i termini noti come 's'  $$ A ( x +  \frac{D}{2A} )^2  + C (y +  \frac{E}{2C}    )^2 = s $$  Per Questa è anche la condizione di realtà dell'ellisse $ s>0 $  $$ s = \frac{D^2}{4A} +  \frac{E^2}{4C} - F $$ perché l'ellisse esiste se $ s>0 $. Se $ s=0 $ l'ellisse degenera in un punto mentre l'iperbole in una coppia di rette. Se s<0 l'ellisse non esiste. Tornando all'equazione $$ A ( x +  \frac{D}{2A} )^2  + C (y +  \frac{E}{2C}    )^2 = s $$ posso interpretarla come una translazione della conica dall'origine degli assi cartesiani (0;0) per un vettore $ \left( -  \frac{D}{2A}; - \frac{E}{2C} \right) $ che rappresenta il centro della conica e tornare all'equazione canonica $$ Ax^2 + Cy^2= s $$ che a seconda del segno concorde o discorde di A e C rappresenta rispettivamente un'ellisse o un'iperbole.

Un esempio

Prendo come esempio l'equazione di secondo grado

$$ -2x^2 + y^2 - 6x - 5y +3 = 0 $$

Devo capire se è una conica.

In questo caso A=-2, B=0, C=1, D=-6, E=-5, F=3

Poiché B=0 e A≠C con A≠0 e C≠0 deduco che potrebbe trattarsi di un'iperbole perché A e C sono discordi (A·C<0) ossia hanno il segno opposto.

Applico il metodo del completamento del quadrato.

$$ (-2x^2- 6x) + (y^2  - 5y) +3 = 0 $$

$$ -2(x^2+ 3x) + (y^2  - 5y) +3 = 0 $$

$$ -2(x^2+ 3x + (\frac{3}{2} )^2  -  (\frac{3}{2} )^2) + (y^2  - 5y + (\frac{5}{2} )^2 - (\frac{5}{2} )^2) +3 = 0 $$

$$ -2(x^2+ 3x + (\frac{3}{2} )^2  ) + (y^2  - 5y + (\frac{5}{2} )^2 ) +3 -   (\frac{3}{2} )^2 \cdot (-2) - (\frac{5}{2} )^2 = 0 $$

$$ -2(x + \frac{3}{2}  )^2 + (y  -  \frac{5}{2}  )^2 +  3 -  \frac{9}{4} \cdot (-2) - \frac{25}{4}= 0 $$

$$ -2(x + \frac{3}{2}  )^2 + (y  -  \frac{5}{2}  )^2 +  3 +  \frac{9}{2}- \frac{25}{4}= 0 $$

$$ -2(x + \frac{3}{2}  )^2 + (y  -  \frac{5}{2}  )^2 +   \frac{12+18-25}{4}= 0 $$

$$ -2(x + \frac{3}{2}  )^2 + (y  -  \frac{5}{2}  )^2 +   \frac{5}{4}= 0 $$

$$ -2(x + \frac{3}{2}  )^2 + (y  -  \frac{5}{2}  )^2 = -   \frac{5}{4} $$

La riconduco all'equazione canonica dell'ellisse moltiplicando entrambi i lati per -1

$$ (-1) \cdot [ -2(x + \frac{3}{2}  )^2 + (y  -  \frac{5}{2}  )^2 ] = -(1) \cdot ( -   \frac{5}{4} ) $$

$$ 2(x + \frac{3}{2}  )^2 - (y  -  \frac{5}{2}  )^2 ] =  \frac{5}{4} $$

Quest'ultima è l'equazione di una iperbole con centro in $ \left(  - \frac{3}{2} ;  \frac{5}{2}  \right) $ e l'asse trasverso, quello con i fuochi, parallello all'asse x.

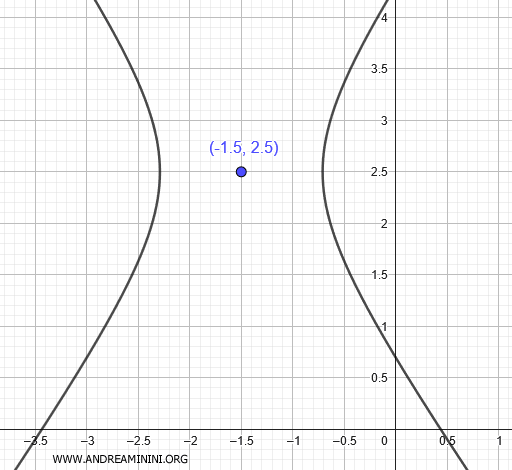
Esempio 2

Considero l'equazione di secondo grado

$$ 4x^2 +9y^2 -5x-y+10 = 0 $$

Devo capire se si tratta di una conica oppure no.

In questo caso A=4, B=0 , C=9, D=-5, E=-1, F=10

Poiché B=0 e A≠C con A≠0 e C≠0 deduco che potrebbe trattarsi di un'ellisse perché A e C sono concordi (A·C<0) ossia hanno lo stesso segno.

Raccolgo le variabili x e y

$$ (4x^2-5x) + (9y^2-y)+10 = 0 $$

Poi completo i quadrati

$$ (4x^2-5x + (\frac{5}{4})^2- (\frac{5}{4})^2 ) + (9y^2-y + (\frac{1}{6})^2-(\frac{1}{6})^2)+10 = 0 $$

$$ (4x^2-5x + (\frac{5}{4})^2 ) + (9y^2-y + (\frac{1}{6})^2)+10 - (\frac{5}{4})^2 -(\frac{1}{6})^2= 0 $$

$$ (2x-\frac{5}{4})^2 + (3y - \frac{1}{6})^2 +10 - \frac{25}{16} - \frac{1}{36} = 0 $$

$$ (2x-\frac{5}{4})^2 + (3y - \frac{1}{6})^2 +10 - \frac{25}{16} - \frac{1}{36} = 0 $$

$$ (2x-\frac{5}{4})^2 + (3y - \frac{1}{6})^2 +\frac{1440-225-4}{144} = 0 $$

$$ (2x-\frac{5}{4})^2 + (3y - \frac{1}{6})^2 +\frac{1211}{144} = 0 $$

$$ (2x-\frac{5}{4})^2 + (3y - \frac{1}{6})^2 = - \frac{1211}{144}  $$

In questo caso però la condizione di esistenza dell'ellisse non è soddifatta perché il termine noto nel lato destro è negativo

$$ s = - \frac{1211}{144}  < 0 $$

Quindi, questa equazione non è una conica.

La dimostrazione

Considero una retta direttrice \( ax + by + c = 0 \) e un punto generico \( P(x; y) \) della conica che non appartiene a questa retta.

Per definizione una conica è il luogo geometrico dei punti \( P(x, y) \) tali che il rapporto tra la distanza di \( P \) da un punto fisso \( F \) (il fuoco) e la distanza di \( P \) da una retta fissa \( d \) (la direttrice) è costante ed è chiamato eccentricità \( e \):

$$ \frac{ \overline{PF} }{ \overline{PH} } = e $$

$$ \overline{PF}= \overline{PH} \cdot e $$

La distanza PF tra il punto P(x;y) e un punto fisso detto fuoco $ F(p;q) $ della conica è la seguente:

$$ \overline{PF} = \sqrt{(x-p)^2 + (y-q)^2}  $$

La distanza PH tra il punto P(x;y) e l'equazione della retta direttrice $ ax+by+c=0 $ dove x e y sono le coordinate del punto P è la seguente:

$$ \overline{PH} = \frac{|ax+by+c|}{ \sqrt{a^2 + b^2} }    $$

Sostituisco le espressioni delle distanze

$$ \overline{PF}= \overline{PH} \cdot e $$

$$ \sqrt{(x-p)^2 + (y-q)^2} = \frac{|ax+by+c|}{ \sqrt{a^2 + b^2} }  \cdot e $$

Elevo al quadrato entrambi i lati dell'equazione

$$ ( \sqrt{(x-p)^2 + (y-q)^2}  )^2 = ( \frac{|ax+by+c|}{ \sqrt{a^2 + b^2} }  \cdot e )^2 $$

$$ (x-p)^2 + (y-q)^2 = \frac{(|ax+by+c|)^2}{ ( \sqrt{a^2 + b^2} )^2 }  \cdot e^2 $$

$$ (x-p)^2 + (y-q)^2 = \frac{(ax+by+c)^2}{ a^2 + b^2}   \cdot e^2 $$

Espando i quadrati e riorganizzo i termini:

$$ (x^2 - 2xp + p^2) + (y^2 - 2yq + q^2) = \frac{e^2}{a^2 + b^2} \cdot (a^2x^2 + 2abxy + b^2y^2 + 2acx + 2bcy + c^2) $$

Raggruppo i termini simili e portando tutto sullo stesso lato dell'equazione, ottenendo così una forma generale:

$$ [(1-e^2)a^2 + b^2]x^2 + 2abe^2xy + [(1-e^2)b^2 + a^2]y^2 \\ - 2(a^2p + b^2p + ace)x - 2(a^2q + b^2q + bce)y \\ + (p^2 + q^2)(a^2 + b^2) - c^2e^2 = 0 $$

L'espressione ottenuta può essere scritta nella forma generale dell'equazione di una conica:

$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$

Dove i coefficienti \( A \), \( B \), \( C \), \( D \), \( E \) e \( F \) sono determinati in funzione di \( a \), \( b \), \( c \), \( p \), \( q \) ed \( e \).

• $ A = (1-e^2)a^2 + b^2 $
• $ B = 2abe^2 $
• $ C =(1-e^2)b^2 + a^2 $
• $ D = - 2(a^2p + b^2p + ace) $
• $ E = - 2(a^2q + b^2q + bce) $
• $ F = (p^2 + q^2)(a^2 + b^2) - c^2e^2 $

Questa equazione rappresenta una conica che può essere un'ellisse, una parabola o un'iperbole a seconda del valore dell'eccentricità \( e \).

• Se \( e = 0 \), la conica è una circonferenza.
• Se \( 0 < e < 1 \), la conica è un'ellisse.
• Se \( e = 1 \), la conica è una parabola.
• Se \( e > 1 \), la conica è un'iperbole.

In questo modo, partendo dalla definizione della conica e dalle formule di distanza, sono arrivato all'equazione generale della conica nel piano cartesiano.

Le coniche immaginarie e degeneri

L’equazione generale di secondo grado \[ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0, \qquad (A,B,C \ \text{non tutti nulli}) \] si classifica in base al discriminante \(\Delta = B^2 - 4AC\).

Questo parametro distingue le tre grandi famiglie di coniche:

• se \(\Delta < 0\), la curva è di tipo ellittico (ellisse o circonferenza);
• se \(\Delta = 0\), la curva è di tipo parabolico (parabola);
• se \(\Delta > 0\), la curva è di tipo iperbolico (iperbole).

Tuttavia, il discriminante da solo non è sufficiente. Infatti non garantisce né che l’equazione abbia soluzioni reali, né che la conica sia effettivamente non degenere.

In altre parole, il discriminante mi dice solo a quale famiglia appartiene l'equazione (ellittica, parabolica, iperbolica). Non mi dice se la conica è immaginaria (non si vede sul piano cartesiano) o degenera in una retta.

Ad esempio, con \(\Delta < 0\) si può avere tanto un’ellisse reale quanto un’ellisse immaginaria (nessun punto reale). Con \(\Delta = 0\) oltre alla parabola compaiono le coppie di rette parallele. Con \(\Delta > 0\) l’iperbole può ridursi a due rette reali concorrenti.

Per individuare i casi degeneri devo usare la matrice simmetrica associata all’equazione:

\[ Q = \begin{pmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{pmatrix}. \]

Il suo determinante è l’invariante che discrimina tra coniche non degeneri e degeneri:

• se \(\det(Q) \neq 0\), la curva è una conica reale non degenere (ellisse, parabola o iperbole);
• se \(\det(Q) = 0\), l’equazione rappresenta una conica degenere, ossia una configurazione di rette (concorrenti, parallele o immaginarie, a seconda del segno di \(\Delta\)).

Il determinante della matrice simmetrica mi fa sapere se la conica è degenere (coppia di rette reali, parallele o immaginarie) oppure no.

Nota. Il determinante della matrice (Q) mi dice solo se la conica è non degenere o degenere ma non garantisce l’esistenza di punti reali. Anche con \( \det(Q) \neq 0 \) potrei avere una conica immaginaria, cioè un’equazione senza soluzioni reali (ad esempio \(x^2 + y^2 + 1 = 0\) ) e invisibile sul piano cartesiano. Per sapere se la conica è effettivamente “disegnabile” nel piano, devo verificare se l’equazione è risolvibile, in pratica controllare se esistono valori reali di (x) e (y) che soddisfano la relazione.

Esempi di classificazione delle coniche

Esempio 1 (ellisse reale)

Considero l'equazione

\[ x^2 + 2y^2 - 4 = 0 \]

Qui \(A=1\), \(B=0\), \(C=2\). Il discriminante è

$$ \Delta = 0^2 - 4\cdot 1 \cdot 2 = -8 < 0 $$

Quindi la conica è di tipo ellittico. L’equazione ha soluzioni reali e rappresenta un’ellisse reale con semiassi \(\sqrt{4}\) e \(\sqrt{2}\).

Esempio 2 (ellisse immaginaria e nessun punto reale)

Prendo come esempio quest'altra equazione:

\[ x^2 + y^2 + 1 = 0 \]

In questo caso \(A=1\), \(B=0\), \(C=1\). Il discriminante è

$$ \Delta = 0 - 4 \cdot 1 \cdot 1 = -4 < 0 $$

La curva è di tipo ellittico, ma l’equazione non ha soluzioni reali: è un’ellisse immaginaria.

Cos'è una conica immaginaria? In parole povere, una conica immaginaria è una curva che sulla carta “esiste” come equazione, ma in realtà non si vede sul piano cartesiano perché non ha nessun punto da disegnare. Quindi rimane solo un oggetto algebrico, non geometrico.

Esempio 3 (parabola)

Considero l'equazione

\[ y - x^2 = 0 \]

Qui \(A=1\), \(B=0\), \(C=0\). Il discriminante è

$$ \Delta = 0^2 - 4\cdot 1 \cdot 0 = 0 $$

Quindi la conica è di tipo parabolico. L’equazione rappresenta la parabola con asse verticale.

Esempio 4 (coppia di rette parallele)

Considero l’equazione:

\[ x^2 - 1 = 0 \]

I coefficienti sono: \(A=1\), \(B=0\), \(C=0\), \(D=0\), \(E=0\), \(F=-1\) e il discriminante è:

\[ \Delta = B^2 - 4AC = 0^2 - 4 \cdot 1 \cdot 0 = 0 \]

Quindi la curva è di tipo parabolico.

Tuttavia, per studiarla meglio, costruisco la matrice associata \(Q\):

\[ Q = \begin{pmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{pmatrix} \]

Il determinante della matrice è:

\[ \det(Q) = \begin{vmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{vmatrix} = 1 \cdot (0 \cdot -1 - 0 \cdot 0) = 0 \]

Poiché \(\det(Q) = 0\) è nullo, la conica è degenere. Infatti l’equazione si fattorizza come:

\[ x^2 - 1 = (x-1)(x+1) = 0 \]

La curva non è una parabola, ma la coppia di rette parallele verticali \(x=1\) e \(x=-1\).

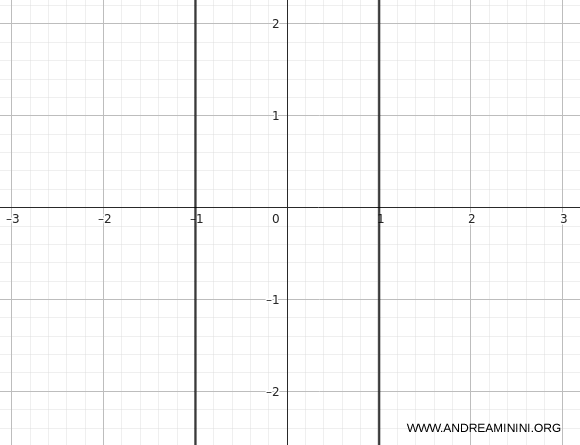
Esempio 5 (iperbole)

Considero l'equazione

\[ x^2 - y^2 - 1 = 0 \]

Qui \(A=1\), \(B=0\), \(C=-1\). Il discriminante è \(\Delta = 0 - 4\cdot 1 \cdot (-1) = 4 > 0\), quindi la curva è di tipo iperbolico.

L’equazione rappresenta un’iperbole con asintoti \(y = \pm x\).

Esempio 6 (coppia di rette reali concorrenti)

Considero l'equazione seguente:

\[ x^2 - y^2 = 0 \]

I coefficienti sono: \(A=1\), \(B=0\), \(C=-1\), \(D=0\), \(E=0\), \(F=0\).

Il discriminante è:

\[ \Delta = B^2 - 4AC = 0^2 - 4 \cdot 1 \cdot (-1) = 4 > 0 \]

Quindi la curva è di tipo iperbolico.

Ora costruisco la matrice associata \(Q\):

\[ Q = \begin{pmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{pmatrix} \]

Il determinante della matrice è nullo.

\[ \det(Q) = \begin{vmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{vmatrix} = 1 \cdot (-1) \cdot 0 = 0 \]

Poiché \(\det(Q) = 0\), la conica degenera in due rette. Infatti l’equazione si può fattorizzare come:

\[ x^2 - y^2 = (x-y)(x+y) = 0 \]

La curva non è un’iperbole vera e propria, ma una coppia di rette reali concorrenti \(y=x\) e \(y=-x\).

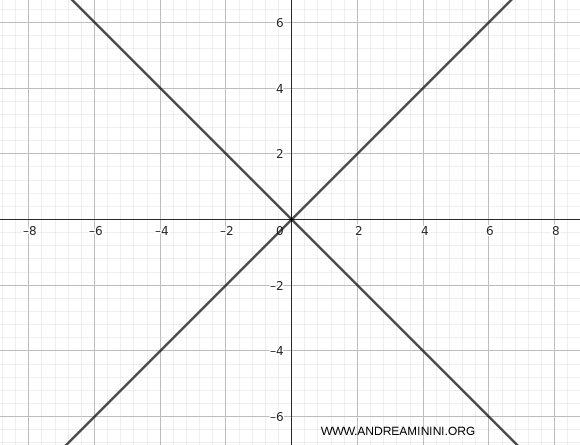
Note aggiuntive

Alcune note a margine sulle coniche.

• Eliminare il termine misto xy dall'equazione di una conica
  Per eliminare il termine misto $ xy $ di una conica, basta ruotare gli assi di un angolo $ \alpha $ che soddisfa la condizione $$ \tan 2 \alpha = \frac{B}{A-C} $$ Dove $ A, B, C $ sono i coefficienti dell'equazione generale della conica.

  Nota. Se il denominatore $ A-C=0 $ è nullo, allora (\tan 2\alpha) non esiste perché l'angolo è verticale, in questo caso particolare la condizione diventa semplicemente (\cos 2\alpha = 0), cioè (2\alpha = \pi/2 + k\pi). 

E così via.