Distanza di un punto da un piano

La distanza tra un punto P e un piano è data dalla lunghezza del segmento perpendicolare che congiunge P al piano.

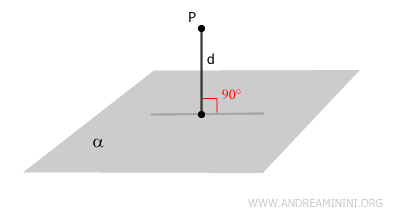
In altre parole, la distanza tra un punto P e un piano è uguale alla lunghezza del segmento perpendicolare al piano che ha per estremi il punto P e un punto qualsiasi del piano.

La distanza è sempre un valore non negativo. Se il punto appartiene al piano la distanza è nulla.

Come calcolare la distanza tra un punto e il piano

 

La distanza minima tra un punto P e un piano α nello spazio è data dalla lunghezza del segmento perpendicolare al piano α che ha origine in P.

$$ d(P, \alpha ) = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} $$

Esempio

Considero il punto P alle coordinate (x;y;z)=(1;3;2) nello spazio a tre dimensioni

$$ P = \begin{pmatrix} 1 \\ 3 \\ 2 \end{pmatrix} $$

L'equazione cartesiana del piano è la seguente:

$$ 4x-2y+z-5 = 0 $$

La distanza tra il punto e il piano si calcola usando la formula precedente.

$$ d(P,a) = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} $$

Indico i parametri dell'equazione del piano a=4, b=-2, c=1 e d=-5

$$ d(P,a) = \frac{|4 \cdot x_0-2 \cdot y_0+1 \cdot z_0-5|}{\sqrt{4^2+(-2)^2+1^2}} $$

$$ d(P,a) = \frac{|4 \cdot x_0-2 \cdot y_0+1 \cdot z_0-5|}{\sqrt{16+4+1}} $$

$$ d(P,a) = \frac{|4 \cdot x_0-2 \cdot y_0+1 \cdot z_0-5|}{\sqrt{21}} $$

Inserisco le coordinate del punto x₀=1, y₀=3, z₀=2

$$ d(P,a) = \frac{|4 \cdot 1-2 \cdot 3+1 \cdot 2-5|}{\sqrt{21}} $$

$$ d(P,a) = \frac{|-5|}{\sqrt{21}} $$

$$ d(P,a) = \frac{5}{\sqrt{21}} = 1,09 $$

Pertanto la distanza tra il punto P e il piano è 1,09.

Nella rappresentazione grafica seguente è la linea rossa tra il punto P e il piano.

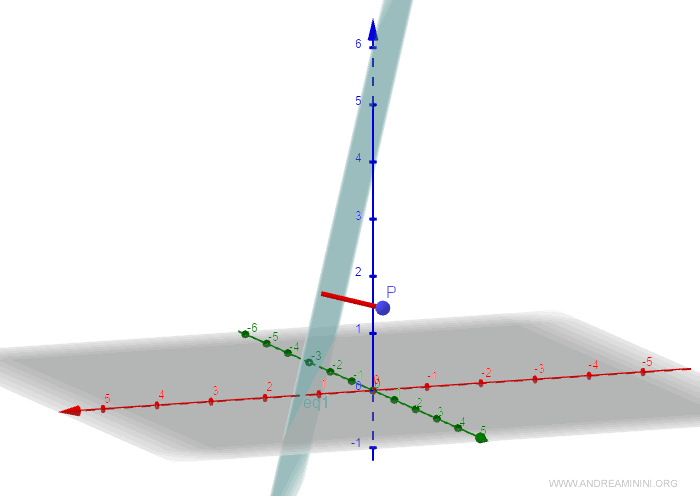
E' la lunghezza del segmento perpendicolare al piano che ha origine nel punto P.

Note

Alcune note aggiuntive sulla distanza tra un punto e il piano

• Teorema
  Dato un piano \( \alpha \) e un punto \( P \) non appartenente al piano \( \alpha \), il segmento perpendicolare \( PH \) condotto da \( P \) al piano è minore di ogni altro segmento obliquo \( PQ \).
  

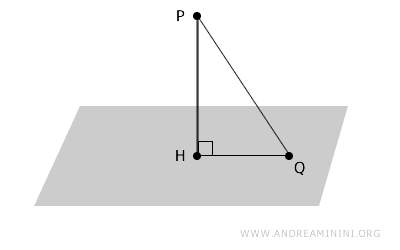
  Dimostrazione. Considero il segmento perpendicolare $ PH $ condotto da $ P $ al piano \( \alpha \) e un qualsiasi lato obliquo $ PQ $ dove $ Q $ è un punto qualsiasi del piano \( \alpha \). I tre punti formano un triangolo rettangolo $ PHQ $. Secondo il teorema di Pitagora, il lato obliquo è sempre più lungo dei singoli cateti, quindi $ PQ > PH $. Da questo deduco che il segmento $ PH $ perpendicolare al piano è la distanza minima tra il punto $ P $ e il piano.

• Corollario
  Dato un piano \( \alpha \) e un punto \( P \) non appartenente al piano \( \alpha \), se due segmenti obliqui condotti da \( P \) al piano hanno proiezioni congruenti, allora sono segmenti congruenti, e viceversa. 
  

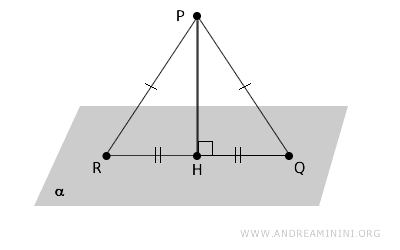
  Dimostrazione. Considero due segmenti obliqui $ PQ \cong PR $ congruenti e un segmento perpendicolare $ PH$, condotti dal punto $ P $ al piano $ \alpha $. In base ai criteri di congruenza dei triangoli, i due triangoli $ PHR \cong PHQ $ sono congruenti perché hanno due lati uguali e un angolo congruente. Quindi, i lati $ HR \cong HQ $ sono congruenti, ovvero i lati obliqui $ PR \cong PQ $ congruenti hanno proiezioni congruenti $ HR \cong HQ $  sul piano $ \alpha $.

• Corollario
  Dato un piano \( \alpha \) e un punto \( P \) non appartenente al piano \( \alpha \), se due segmenti obliqui condotti da \( P \) al piano hanno proiezioni diseguali, allora sono diseguali ed è maggiore quello che ha la proiezione maggiore.
  

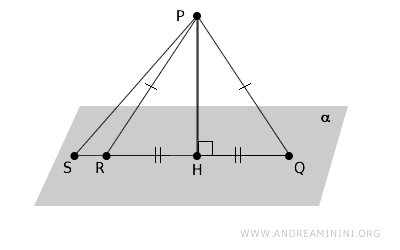
  Esempio. In questo caso il lato obliquo $ PS $ è più lungo di $ PR $, di conseguenza anche la sua proiezione $ HS $ è maggiore dell'altra, overo $ HS > HR $.

E così via.