Coefficiente angolare
Il coefficiente angolare di una retta $$ y=mx + q $$ è il rapporto tra la differenza delle ordinate (yB-yA) e la differenza delle ascisse (xB-xA) di due punti distinti della retta. $$ m = \frac{y_B-y_A}{x_B-x_A} $$ 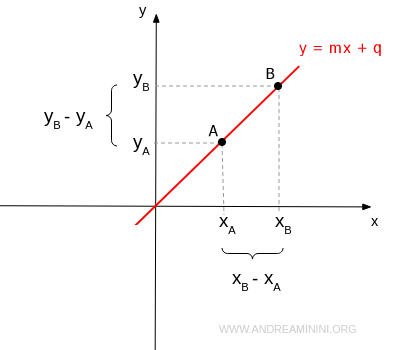
Il coefficiente angolare della retta misura l'inclinazione (o pendenza) della retta rispetto all'asse delle ascisse (x).
Fornisce l'ampiezza dell'angolo α fra la retta e l'asse x che ha per vertice il loro punto di intersezione e per lati la semiretta positiva dell'asse x e la semiretta della retta con ordinata positiva o nulla.
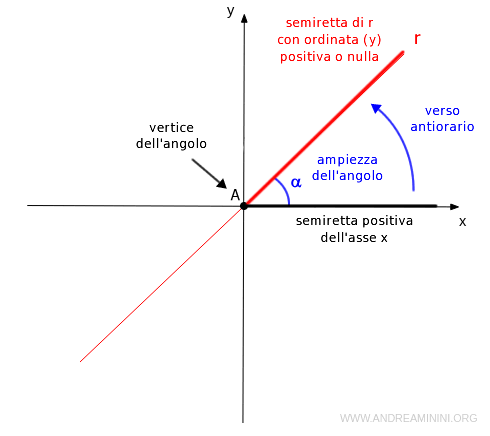
Nota. Per convenzione l'ampiezza di un angolo si misura in senso antiorario a partire dall'asse x positivo.
Il coefficiente angolare di una retta può essere positivo, negativo o nullo a seconda dell'inclinazione della retta.
- Se il coefficiente angolare è positivo (m>0) la retta è crescente. Tra la retta e l'asse delle ascisse si forma un angolo acuto.
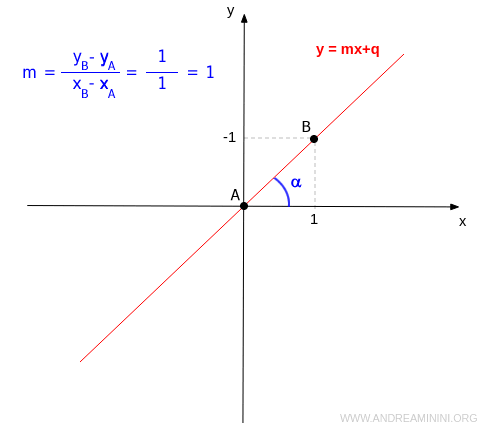
- Se il coefficiente angolare è negativo (m<0) la retta è decrescente. Tra la retta e l'asse delle ascisse si forma un angolo ottuso.
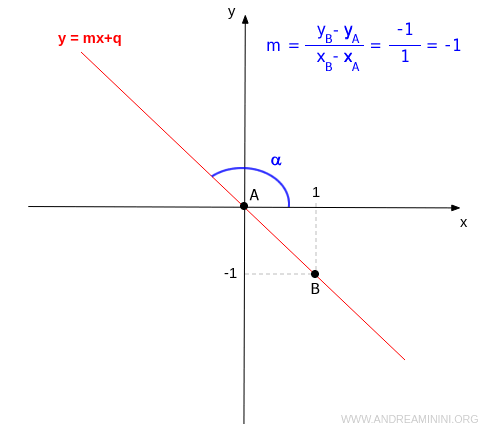
- Se il coefficiente angolare è nullo (m=0) la retta è costante. La retta è parallela o coincidente con l'asse delle ascisse. Quindi, l'angolo è nullo tra la retta e l'ascisse (o qualsiasi altra retta parallela all'ascisse).
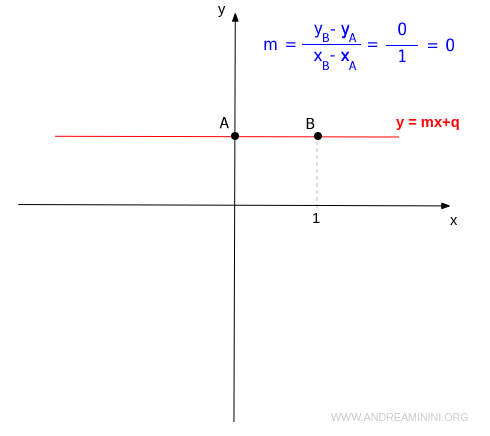
Nota. Il coefficiente angolare non può essere calcolato quando la retta è verticale, ovvero quando è parallela all'asse delle ordinate (y).
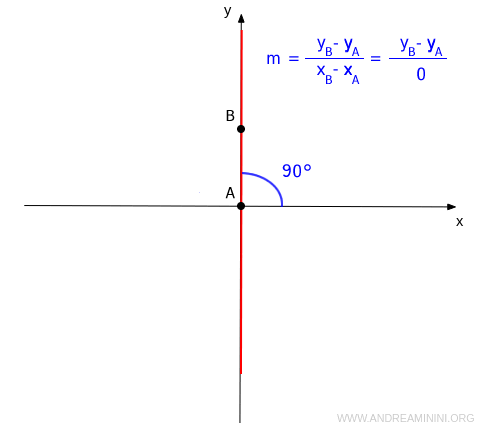
Questo accade perché nel caso in cui x=0 per qualsiasi y si verifica una divisione per zero nel calcolo del coefficiente angolare. $$ m = \frac{y_B-y_A}{x_B-x_A} = \frac{y_B-y_A}{0} $$ Se per assurdo esistesse un quoziente m della divisione per zero m=y/0 allora si dovrebbe avere y=m·0. Tuttavia, questo è impossibile da ottenere perché lo zero è un elemento assorbente, qualsiasi numero moltiplicato per zero è sempre zero y=m·0=0.
Il coefficiente angolare e la tangente dell'angolo
Il coefficiente angolare m di una retta è uguale alla tangente dell'angolo α che la retta forma con l'asse delle ascisse. $$ m = \tan \alpha $$
Questa relazione mi permette di descrivere la pendenza della retta in termini trigonometrici.
E' molto utile per calcolare l'ampiezza dell'angolo α conoscendo il coefficiente angolare della retta, e viceversa.
$$ m = \tan \alpha $$
$$ \alpha = \text{arctan} \ m $$
Dove arctan è l'arcotangente ovvero la funzione trigonometrica inversa della tangente.
Nota. Questa formula richiede la conoscenza della trigonometria e della derivata di una funzione. Quindi, può essere compresa solo a partire dal quinto anno delle scuole superiori o dal primo anno di università. La dimostrazione di questa relazione l'ho già spiegata in un'altra pagina dei miei appunti a cui rimando per ogni approfondimento. Quindi, evito di riscriverla.
Esempio
La retta y=2x-1 ha un coefficiente angolare m=2.
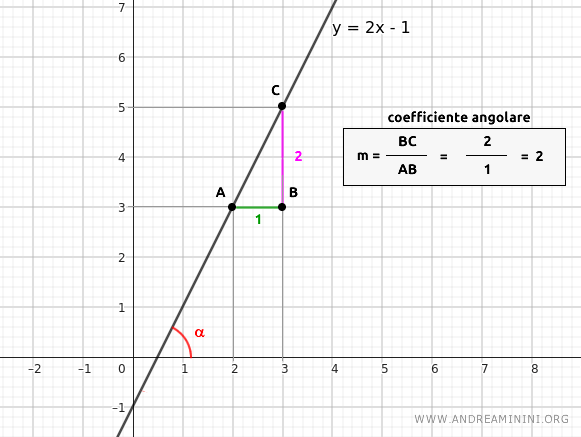
Qual è l'ampiezza dell'angolo α della retta?
Per trovare l'ampiezza devo trovare un valore della tangente uguale al coefficiente angolare m=2.
$$ \tan \alpha = 2 $$
Calcolo l'arcotangente (arctan) di entrambi i membri dell'equazione e ottengo.
$$ \text{arctan}( \tan \alpha ) = \text{arctan} ( 2 ) $$
L'arcotangente è la funzione inversa della tangente (tan), quindi si annullano reciprocamente.
$$ \alpha = \text{arctan} ( 2 ) $$
Quindi, l'ampiezza dell'angolo α è uguale all'arcotangente di 2 che è circa 1.107 radianti.
$$ \alpha_{rad} = 1.107 \ rad $$
Trasformo l'angolo da radianti in gradi usando la formula $ \alpha_{rad} \cdot \frac{180°}{\pi} $
$$ \alpha = 1.107 \ rad \cdot \frac{180°}{\pi} = 63.4264° $$
Pertanto, la retta forma un angolo di ampiezza pari a 63.4264° con l'asse x.
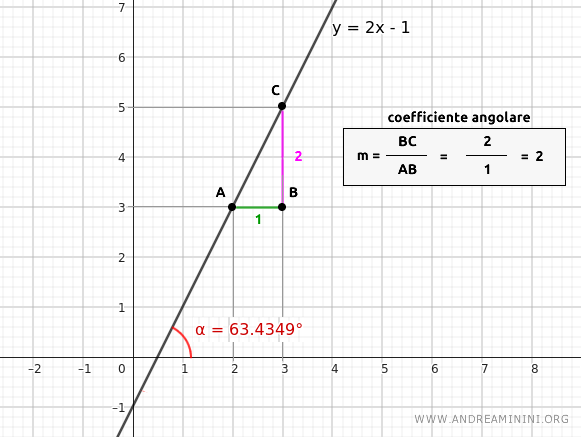
Ho così ottenuto l'ampiezza dell'angolo α della retta a partire dal coefficiente angolare.
E così via.
