L'equazione della retta
L'equazione della retta in forma esplicita è $$ y=m \cdot x + q $$ Dove m è il coefficiente angolare mentre q è il termine noto (o ordinata dell'origine) e indica l'intersezione della retta con l'asse delle ordinate (y).
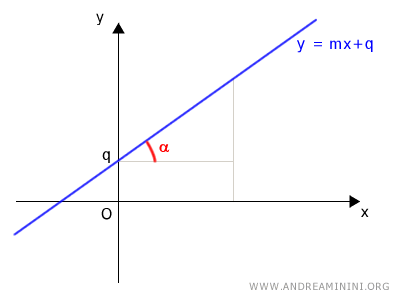
E' detta in forma esplicita perché la variabile y è esplicitata in funzione della variabile x.
$$ y = mx + q $$
Dove y è la variabile dipendente mentre x è la variabile indipendente.
Al variare del coefficiente angolare m cambia l'inclinazione della retta.
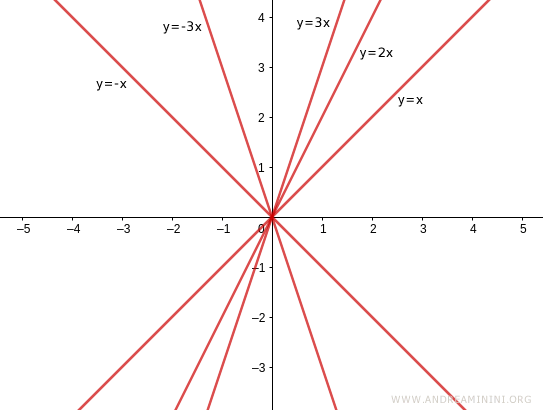
Al variare del termine noto q cambia l'intersezione della retta sull'asse delle ordinate.
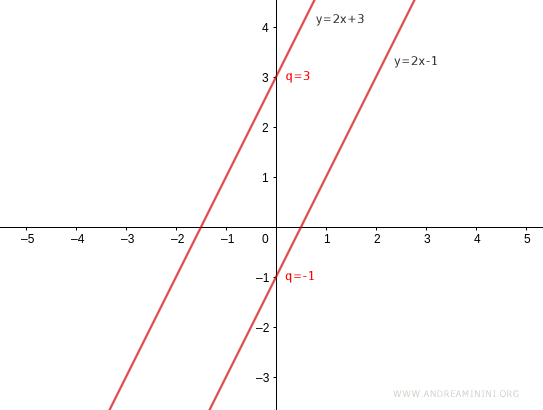
In questo modo, l'equazione della retta in forma esplicita può rappresentare tutte le rette del piano tranne le rette parallele o coincidenti con l'asse y.
Il caso delle rette parallele o coincidenti con l'asse y
Nel caso dell'asse delle ordinate si usa un'equazione diversa
$$ x = 0 $$
Mentre per le rette parallele all'asse y si utilizza l'equazione x=k
$$ x = k $$
Nota. L'asse y non è rappresentabile con l'equazione della retta in forma esplicita y=mx+q perché il coefficiente angolare (m) non è calcolabile quando la retta è perfettamente verticale.
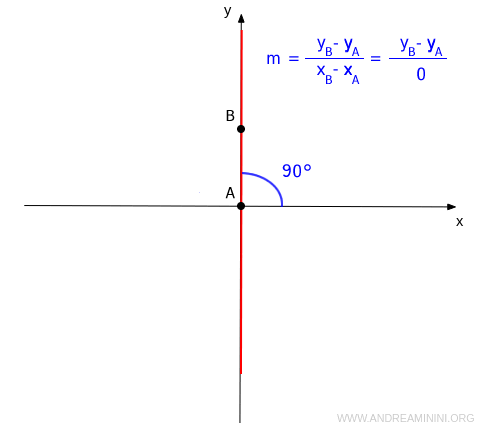
Non esistono valori del coefficiente angolare (m) e del termine noto (q) che sostituiti all'equazione y=mx+q possano rappresentare una qualsiasi retta verticale. Per questa ragione qualsiasi retta parallela all'asse delle ordinate si indica con l'equazione $$ x = k $$ Al variare di k si ottengono tutte le rette parallele all'asse delle ordinate per qualsiasi valore della variabile y. Per k=0 si ottiene l'asse delle ordinate.
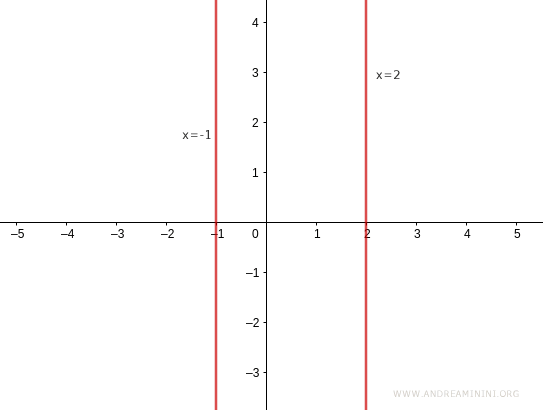
L’equazione in forma implicita
L'equazione della retta in forma implicita è un altro modo di rappresentare le rette del piano $$ ax+ by+c = 0 $$ Dove a, b, c sono numeri reali detti coefficienti. E' anche detta equazione generale della retta.
Nella forma implicita nessuna delle variabili x e y è ricavata in funzione dell'altra.
Al variare dei coefficienti a, b, c l'equazione della retta in forma implicita può rappresentare qualsiasi retta del piano cartesiano.
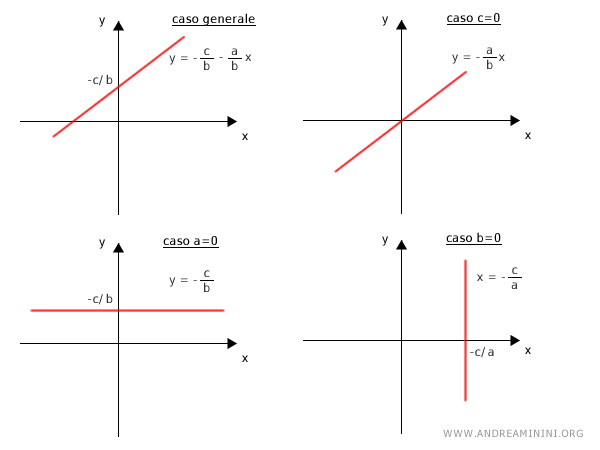
Attenzione. I coefficienti a e b dell'equazione in forma implicita ax+bx+c=0 non devono essere entrambi nulli.
L'equazione della retta in forma implicita può rappresentare anche le rette parallele o coincidenti con l'asse y.
Per questa ragione è anche detta equazione generale della retta.
Nota. Per rappresentare il caso di una retta verticale metto a zero il coefficiente b=0 ed esplicito la variabile x. $$ ax+ by + c = 0 $$ $$ ax+ 0 \cdot y + c = 0 $$ $$ ax+ c = 0 $$ $$ x = - \frac{c}{a} $$
Dimostrazione
Considero due punti P1(x1;y1) e P2(x2;y2) del piano cartesiano in cui passa una retta r non parallela agli assi e un punto P(x;y) intermedio tra P1 e P2 sulla retta.
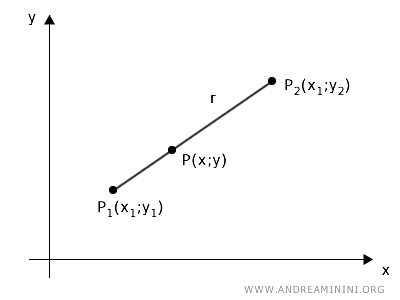
Proietto i punti sugli assi x e y tramite due fasci di rette parallele.
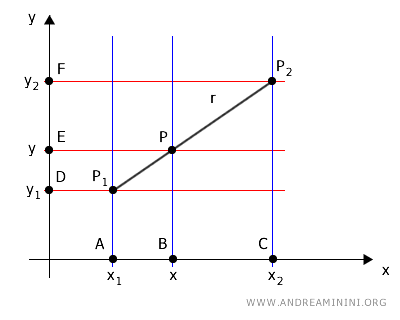
Il fascio di rette verticali che ho colorato in blu, quelle parallele all'asse y, intersecano due trasversali: la retta r e l'asse x.
Quindi, secondo il teorema di Talete i segmenti corrispondenti sulle trasversali sono direttamente proporzionali tra loro.
$$ \frac{ \overline{P_1P} }{ \overline{AB} } = \frac{ \overline{P_1P_2} }{ \overline{AC} } $$
$$ \frac{ \overline{P_1P} }{ \overline{P_1P_2} } = \frac{ \overline{AB} }{ \overline{AC} } $$
Allo stesso modo il fascio di rette orizzontali che ho colorato in rosso, quelle parallele all'asse x, intersecano due trasversali: la retta r e l'asse y.

Sempre secondo il teorema di Talete i segmenti corrispondenti sulle trasversali sono direttamente proporzionali tra loro.
$$ \frac{ \overline{P_1P} }{ \overline{DE} } = \frac{ \overline{P_1P_2} }{ \overline{DF} } $$
$$ \frac{ \overline{P_1P} }{ \overline{P_1P_2} } = \frac{ \overline{DE} }{ \overline{DF} } $$
Da queste due proporzioni deduco l'uguaglianza tra i rapporti AB/AC=DE/EF
$$ \frac{ \overline{P_1P} }{ \overline{P_1P_2} } = \frac{ \overline{AB} }{ \overline{AC} } = \frac{ \overline{DE} }{ \overline{DF} } $$
ovvero
$$ \frac{ \overline{AB} }{ \overline{AC} } = \frac{ \overline{DE} }{ \overline{DF} } $$
Sapendo che AB=x-x1 e AC=x2-x1.
$$ \frac{ x-x_1 }{ x_2-x_1 } = \frac{ \overline{DE} }{ \overline{EF} } $$
Inoltre, sapendo che DE=y-y1 e DF=y2-y1.
$$ \frac{ x-x_1 }{ x_2-x_1 } = \frac{ y - y_1 }{ y_2 - y_1 } $$
Quest'ultima relazione è detta condizione di allineamento di tre punti in una retta.
Con qualche passaggio algebrico modifico la relazione precedente.
$$ ( x-x_1 ) \cdot (y_2 - y_1 ) = (y-y_1) \cdot (x_2-x_1) $$
$$ x \cdot (y_2 - y_1 ) - x_1 \cdot (y_2 - y_1 ) = y \cdot (x_2-x_1) - y_1 \cdot (x_2-x_1) $$
$$ x \cdot (y_2 - y_1 ) - x_1 \cdot (y_2 - y_1 ) - y \cdot (x_2-x_1) + y_1 \cdot (x_2-x_1) = 0 $$
$$ \require{cancel} x \cdot (y_2 - y_1 ) - y \cdot (x_2-x_1) - x_1y_2 + \cancel{ x_1y_1 } + x_2y_1 - \cancel{ x_1y_1 }= 0 $$
$$ x \cdot (y_2 - y_1 ) - y \cdot (x_2-x_1) - x_1y_2 + x_2y_1 = 0 $$
Trasformo -y(x2-x1) nella forma equivalente +y(x1-x2)
$$ x \cdot (y_2 - y_1 ) + y \cdot (x_1-x_2) - x_1y_2 + x_2y_1 = 0 $$
A questo punto indico con a=(y2-y1), b=(x1-x2), c=-x1y2+x2y1
$$ x \cdot a + y \cdot b +c = 0 $$
In questo modo ottengo la forma implicita dell'equazione della retta.
$$ ax + by +c = 0 $$
Come passare dalla forma implicita a quella esplicita
Per passare dall’equazione in forma implicita $ ax+by+c=0 $ a quella in forma esplicita $ y = mx+q $ mi basta esplicitare la variabile y.
$$ y = - \frac{ax}{b} - \frac{c}{b} $$
$$ y = - \frac{a}{b} \cdot x - \frac{c}{b} $$
Dove -a/b è il coefficiente angolare e -c/b è il termine noto.
$$ m = - \frac{a}{b} $$
$$ q = - \frac{c}{b} $$
Questo è possibile soltanto se il coefficiente b è diverso da zero.
Nota. La trasformazione dalla forma implicita a quella esplicita non è possibile se il coefficiente b=0 è nullo, perché si verifica una divisione per zero.
Esempio
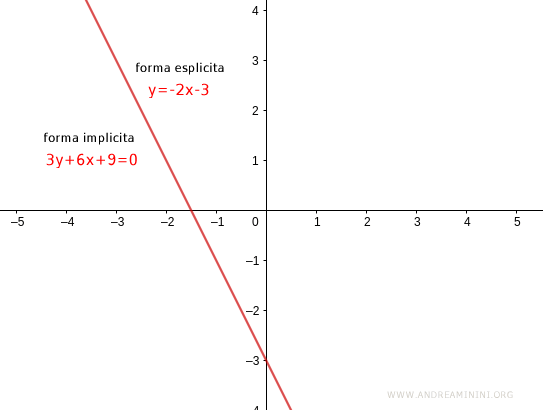
Ho l’equazione della retta in forma implicita dove a=3, b=6 e c=9
$$ 3y + 6x + 9 = 0 $$
Per trasformarla in forma esplicita, esplicito la y rispetto alle altre variabili.
$$ 3y = - 6x - 9 $$
Poi applico la proprietà invariantiva dividendo entrambi i membri dell'equazione per 3
$$ \frac{3y}{3} = - \frac{6}{3}x - \frac{9}{3} $$
$$ y = - 2x - 3 $$
Quest’ultima è l’equazione della retta scritta in forma esplicita .
$$ y = mx + q $$
Dove il coefficiente angolare è m=-2 e il termine noto è q=-3
Qual è la differenza tra la forma implicita e la forma esplicita? Entrambe le forme rappresentano la stessa retta sul piano è sempre la stessa. Cambia solo la forma algebrica per rappresentarla.
La forma implicita della retta come sistema di due piani
Ogni retta nello spazio può essere descritta come l’intersezione di due piani non paralleli, rappresentati da un sistema di due equazioni di primo grado. $$ \begin{cases} a_1 x + b_1 y + c_1 z + d_1 = 0 \\ \\ a_2 x + b_2 y + c_2 z + d_2 = 0 \end{cases} $$
In geometria analitica, una retta nello spazio (cioè in $\mathbb{R}^3$) può essere rappresentata in diversi modi.
Una delle rappresentazioni più semplici è la cosiddetta forma implicita, che consiste nell'esprimere la retta come sistema di due equazioni di piano.
Ogni piano nello spazio ha un'equazione generale:
$$ a x + b y + c z + d = 0 $$
Ora, se considero due piani distinti che si intersecano, posso scrivere un sistema con due equazioni:
$$
\begin{cases}
a_1 x + b_1 y + c_1 z + d_1 = 0 \\ \\
a_2 x + b_2 y + c_2 z + d_2 = 0
\end{cases}
$$
Le equazioni del sistema sono dette equazioni generali della retta e ogni equazione rappresenta un piano.
Questo sistema rappresenta in modo implicito una retta, poiché impone due condizioni sui punti $(x, y, z)$. I punti che soddisfano entrambe le equazioni appartengono simultaneamente ai due piani, e quindi costituiscono la loro intersezione.
L'intersezione di due piani distinti (non paralleli) è una retta $ r $.
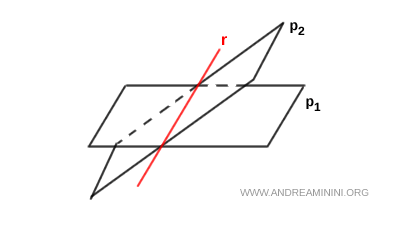
Ovviamente il sistema che rappresenta la retta non è unico, perché esistono infiniti piani che possono intersecarsi dando origine alla stessa retta $ r $.
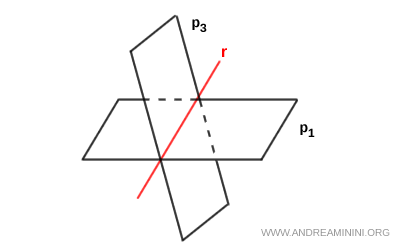
L'insieme delle piani che dà origine alla stessa retta $ r $ forma un fascio di piani.
Perché si chiama forma implicita? Si chiama implicita perché non esplicita le coordinate della retta come funzione di un parametro e non mi fa subito capire se passa per un determinato punto e qual è la direzione. Mi dà invece due vincoli (due piani), e la retta è definita come loro intersezione.
Esempio
Considero i due piani:
$$
\begin{cases}
x + y + z - 1 = 0 \\
2x - y + 3z + 4 = 0
\end{cases}
$$
L'insieme dei punti $(x, y, z)$ che soddisfa entrambe le equazioni è una retta nello spazio.
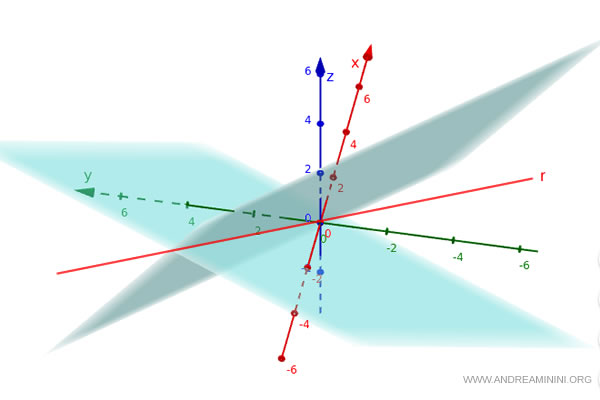
Le equazioni ridotte della retta
Le equazioni ridotte sono un modo per descrivere una retta nello spazio usando due equazioni nelle quali due coordinate sono espresse in funzione della terza.
Ad esempio, la coppia di variabili x e y in funzione di z.
$$
\begin{cases}
a_1 x + b_1 y + c_1 z + d_1 = 0 \\ \\
a_2 x + b_2 y + c_2 z + d_2 = 0
\end{cases} \ \rightarrow \
\begin{cases}
x = g z + p \\ \\
y = hz + q
\end{cases}
$$
Oppure la coppia di variabili x e z in funzione di y
$$
\begin{cases}
x = ky + r \\ \\
z = jy + s
\end{cases}
$$
o la coppia di variabili y e z in funzione di x.
$$
\begin{cases}
y = mx + t \\ \\
z = nx + u
\end{cases}
$$
Questa forma è utile per descrivere la retta in modo parametrico implicito, senza usare direttamente un ulteriore parametro t.
Attribuendo valori arbitrari alla variabile indipendente (come z), si ottengono punti sulla retta.
Nota. La scelta del parametro dipende dalla posizione della retta nello spazio. Ad esempio, se la retta è parallela al piano Oxy, allora la coordinata z resta costante lungo tutta la retta. In questo caso, non si può usare z come parametro per esprimere x e y, perché non varia. $$ \begin{cases} x = g z + p \\ \\ y = hz + q \end{cases} $$ Lo stesso vale se la retta è parallela al piano Oxz o al piano Oyz, in questi casi, non è possibile scegliere rispettivamente la variabile y o x come parametro, poiché rimarrebbero costanti lungo la retta. Quindi, per scrivere le equazioni ridotte della retta, si deve scegliere come parametro una variabile che cambia, cioè che non è costante lungo la retta.
Esempio
Considero la retta espressa dal sistema di equazioni:
$$
\begin{cases}
x + y - z = 0 \quad \text{(1)} \\
2x - y + 3z = 5 \quad \text{(2)}
\end{cases}
$$
Per trovare le equazioni ridotte, devo risolvere il sistema. Scelgo di risolverlo trovando la coppia di variabili $ x $ e $ y $ in funzione della variabile $ z $.
Sommo la prima equazione con la seconda, in questo modo elimino la $ y $ e ricavo $ x $.
$$
\begin{cases}
x+2x + y-y - z+3z = 0+5 \\
2x - y + 3z = 5
\end{cases}
$$
$$
\begin{cases}
3x +2z = 5 \\
2x - y + 3z = 5
\end{cases}
$$
$$
\begin{cases}
x = \frac{5 - 2z}{3} \\
2x - y + 3z = 5
\end{cases}
$$
Ora sostituisco la $ x $ nella seconda equazione e ricavo la variabile $ y $.
$$
\begin{cases}
x = \frac{5 - 2z}{3} \\
2 ( \frac{5 - 2z}{3} ) - y + 3z = 5
\end{cases}
$$
$$
\begin{cases}
x = \frac{5 - 2z}{3} \\
\frac{10 - 4z}{3} - y + 3z = 5
\end{cases}
$$
$$
\begin{cases}
x = \frac{5 - 2z}{3} \\
y = \frac{10 - 4z}{3} - 5 + 3z
\end{cases}
$$
$$
\begin{cases}
x = \frac{5 - 2z}{3} \\
y = \frac{10 - 4z-15+9z}{3}
\end{cases}
$$
Ho così trovato le due equazioni ridotte della retta.
$$
\begin{cases}
x = \frac{5 - 2z}{3} \\
y = \frac{5z-5}{3}
\end{cases}
$$
Per risolvere il sistema si può usare qualsiasi metodo, in questo caso ho trovato utile sommare le due equazioni.
Le equazioni frazionarie e parametriche della retta
Date due punti distinti $A(x_1, y_1, z_1)$ e $B(x_2, y_2, z_2)$, la retta passante per questi due punti ha le seguenti equazioni frazionarie: $$ \frac{x - x_1}{l} = \frac{y - y_1}{m} = \frac{z - z_1}{n} $$ dove: $$ l = x_2 - x_1, \quad m = y_2 - y_1, \quad n = z_2 - z_1 $$ Questi valori $l, m, n$ si chiamano coefficienti direttivi della retta.
Le equazioni frazionarie sono un modo compatto per descrivere una retta nello spazio tridimensionale, perché permettono di esprimere, in un’unica relazione, il legame tra le coordinate $x, y, z$ dei punti della retta.
So già che la condizione di allineamento in una retta nello spazio soddisfa questa condizione:
$$ \frac{ x-x_1 }{ x_2-x_1 } = \frac{ y - y_1 }{ y_2 - y_1 } = \frac{ z - z_1 }{ z_2 -z_1 } $$
Chiamo i denominatori di questa condizione $ l=x_2-x1 $, $ m = y_2 - y_1 $, $ n = z_2 - z_1 $.
$$ \frac{ x-x_1 }{ l } = \frac{ y - y_1 }{ m } = \frac{ z - z_1 }{ n } $$
Questi coefficienti $l, m, n$ sono detti coefficienti direttivi e rappresentano quanto ci si sposta lungo gli assi $x, y, z$ per passare da un punto all’altro sulla retta.
- $l = x_2 - x_1$ indica di quanto aumenta o diminuisce la coordinata $x$ da $A$ a $B$.
- $m = y_2 - y_1$ indica lo spostamento lungo $y$.
- $n = z_2 - z_1$ indica lo spostamento lungo $z$.
I numeri $l, m, n$ indicano come la retta si muove nello spazio lungo gli assi $x, y, z$.
In altre parole, $(l, m, n)$ è il vettore direzione della retta: dice in quale direzione e verso si muove la retta nello spazio.
Nota. Se moltiplico i coefficienti direttivi per uno stesso fattore $k$, la direzione resta la stessa, cioè $(l, m, n)$ e $(k\,l, k\,m, k\,n)$ individuano la stessa retta. Quindi, due rette sono parallele se hanno gli stessi coefficienti direttivi in proporzione $ l = kl' $ $ m=km' $, $ n = kn' $, ossia se valgono le seguenti proporzioni tra i coefficienti direttivi: $$ \frac{l}{l'} = \frac{m}{m'} = \frac{n}{n'} = k $$
Esempio
Considero i punti:
$$ A(1, -2, 3), \quad B(5, 4, 1) $$
Calcolo i coefficienti direttivi:
$$ l = 5 - 1 = 4 $$
$$ m = 4 - (-2) = 6 $$
$$ n = 1 - 3 = -2 $$
Le equazioni frazionarie della retta passante per $A$ e $B$ sono:
$$ \frac{x - 1}{4} = \frac{y + 2}{6} = \frac{z - 3}{-2} $$
L’equazione frazionaria m dice che quando $x$ cresce di $l$, anche $y$ cresce di $m$ e $z$ cresce di $n$.
Ogni rapporto indica quante volte ho percorso il vettore direzione partendo da $A$.
In questo caso il vettore direttore ha le componenti $ \vec{v} = ( 4, 6, -2) $
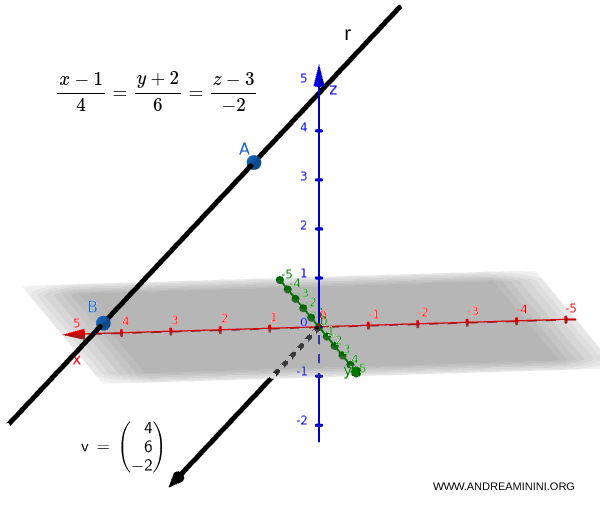
Caso di coefficienti nulli. Se uno dei coefficienti $l, m, n$ è uguale a zero, significa che la retta è parallela a uno dei piani coordinati:
- Se $l = 0$, la retta è parallela al piano $Oyz$ allora $x$ è costante.
- Se $m = 0$, la retta è parallela al piano $Oxz$ allora $y$ è costante.
- Se $n = 0$, la retta è parallela al piano $Oxy$ allora $z$ è costante.
In questi casi, le equazioni frazionarie non possono essere scritte perché ci sarebbe divisione per zero. Si usano invece equazioni ridotte in cui la coordinata costante viene esplicitata.
Le equazioni parametriche
Ponendo tutti i rapporti uguali a un parametro $t$ ottengo
$$ \begin{cases} \frac{x - x_1}{l} = t \\ \frac{y - y_1}{m} = t \\ \frac{z - z_1}{n} = t \end{cases} $$
Ricavo x, y, z da ciascuna equazione
$$ \begin{cases} x - x_1 = lt \\ y - y_1 = mt \\ z - z_1 = nt \end{cases} $$
$$ \begin{cases} x = x_1 + l\,t \\ y = y_1 + m\,t \\ z = z_1 + n\,t \end{cases} $$
Queste sono le equazioni parametriche della retta.
Quindi le equazioni frazionarie rappresentano in forma alternativa delle equazioni parametriche.
Esempio
Considero l'equazione frazionaria dell'esempio precedente
$$ \frac{x - 1}{4} = \frac{y + 2}{6} = \frac{z - 3}{-2} $$
Scrivo un sistema mettendo tutti i rapporti uguali a un parametro t
$$ \begin{cases} \frac{x - 1}{4} = t \\ \\ \frac{y + 2}{6} = t \\ \\ \frac{z - 3}{-2} = t \end{cases} $$
Ricavo la $ x $ dalla prima equazione, la $ y $ dalla seconda e la $ z $ dalla terza
$$ \begin{cases} x = 1+4t \\ \\ y = -2+6t \\ \\ z = 3-2t \end{cases} $$
Queste sono le equazioni parametriche della stessa retta.
Le coordinate polari della retta
- L'equazione della retta posso scriverla anche tramite le coordinate polari.
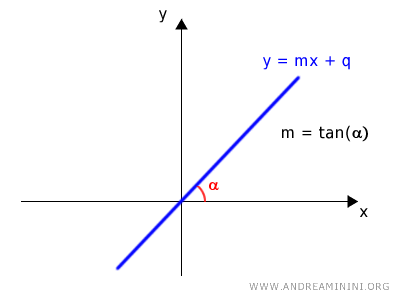
- Se la retta passa per l'origine è sufficiente conoscere l'angolo α che determina il coefficiente angolare $$ m = \tan \alpha \ \ \ \ con \ \alpha \ne \frac{\pi}{2}+k \pi $$
- Se la retta non passa per l'origine è necessario conoscere la distanza d tra la retta e il polo (origine) e l'angolo β del segmento d rispetto al semiasse polare positivo. $$ d = r \cdot \cos (θ) $$
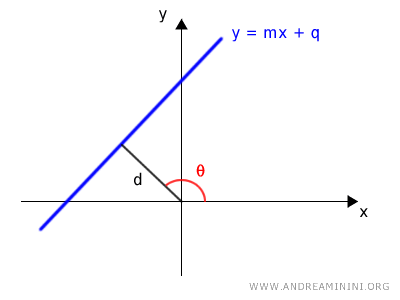
Dove θ α l'angolo delle coordinate polari di un altro punto P qualsiasi della retta.
Osservazioni
Alcune osservazioni e note a margine sull'equazione lineare (equazione della retta).
- L'equazione della retta individua tutti i punti di una e una sola retta
Questa affermazione si dimostra per assurdo, ipotizzando che esista un punto P'(x;y') esterno alla retta r che soddisfa l'equazione lineare ax+by+c=0 della retta r. Per ipotesi, il punto P' ha la stessa ascissa del punto P ma una ordinata diversa.
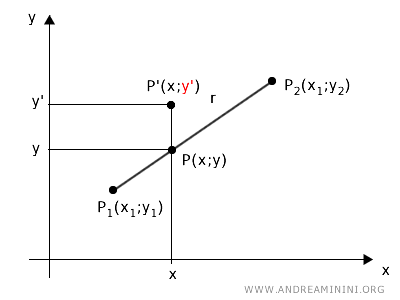
In base a questa ipotesi, sono soddisfatte entrambe le seguenti equazioni: $$ ax+by+c=0 $$ $$ ax+by'+c=0 $$ Per risolvere il sistema utilizzo il metodo della riduzione, sottraggo le due equazioni l'una dall'altra. $$ \begin{matrix} ax & +by & + c & =0 & - \\ ax & +by' & + c & = 0 & \\ \hline 0 & +b(y-y') & 0 & = 0 \end{matrix} $$ Il risultato è l'equazione $$ b(y-y')=0 $$ Sapendo che il coefficiente b è diverso da zero, l'unico modo per soddisfare l'equazione è l'uguaglianza tra le ordinate y=y'. In altre parole il punto esterno P' deve avere anche la stessa ordinata del punto interno P. Questo però contraddice l'ipotesi iniziale in quanto P' è un punto esterno alla retta, mentre P è un punto interno alla retta. In conclusione, è falso che i punti esterni a una retta r soddisfino l'equazione ax+bx+c=0. Pertanto, è vero il contrario. Solo i punti della retta r soddisfano l'equazione lineare ax+bx+c=0. - Ogni equazione lineare corrisponde a una retta e viceversa
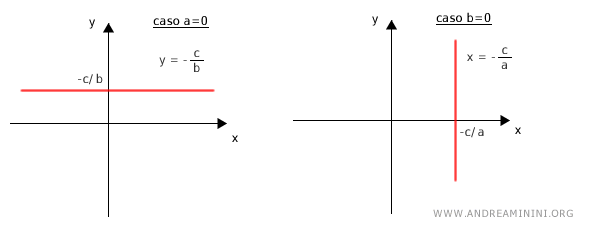
A ogni equazione lineare in due variabili x e y corrisponde una retta del piano cartesiano e viceversa. $$ r \Leftrightarrow ax+by+c=0 $$Dimostrazione. Sapendo che i coefficienti "a" e "b" dell'equazione non devono essere entrambi nulli. Analizzo il caso estremo in cui a=0 e b≠0 e l'altro caso estremo in cui a≠0 e b=0. Nel primo caso ottengo un fascio improprio di rette parallele all'asse orizzontale delle ascisse (x) mentre nel secondo caso un fascio di rette parallele all'asse verticale delle ordinate (y).
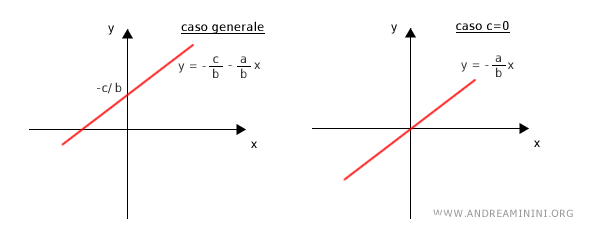
Nel caso intermedio in cui i coefficienti sono non nulli, ovvero a≠0 e b≠0, l'equazione lineare resta nella forma $ ax+by+c=0 $. Devo dimostrare che questa equazione corrisponde a una specifica retta del piano cartesiano. Considero tre punti dell'equazione (x1;y1), (x2;y2), (x3;y3) e li metto in un sistema. $$ \begin{cases} ax_1+by_1+c=0 \\ ax_2+by_2+c=0 \\ ax_3+by_3+c=0 \end{cases} $$ Utilizzo il metodo della riduzione e sottraggo la terza equazione dalla prima e dalla seconda equazione. $$ \begin{cases} a(x_1-x_3)+b(y_1-y_3)=0 \\ a(x_2-x_3)+b(y_2-y_3)=0 \end{cases} $$ $$ \begin{cases} a(x_1-x_3)=-b(y_1-y_3) \\ a(x_2-x_3)=-b(y_2-y_3) \end{cases} $$ $$ \begin{cases} \frac{x_1-x_3}{y_1-y_3}= - \frac{b}{a} \\ \frac{x_2-x_3}{y_2-y_3}= - \frac{b}{a} \end{cases} $$ Confronto le due equazione e capisco che sono entrambe uguali a -b/a. Quindi posso scrivere l'uguaglianza seguente: $$ \frac{x_1-x_3}{y_1-y_3}= \frac{x_2-x_3}{y_2-y_3} $$ che è equivalente alla condizione di allineamento di tre punti di una retta $$ \frac{x_1-x_3}{x_2-x_3}= \frac{y_1-y_3}{y_2-y_3} $$ Questo dimostra che l'equazione lineare $ ax+by+c=0 $ corrisponde a una e una sola retta del piano ovvero c'è una corrispondenza biunivoca tra le soluzioni dell'equazione lineare e i punti di una retta del piano.
E così via.
