Omotetia

L'omotetia è una trasformazione geometrica che mappa i punti di una figura rispetto a un punto fisso O, modificando le distanze relative tra i punti in proporzione a un fattore k, lasciando inalterata la forma della figura.

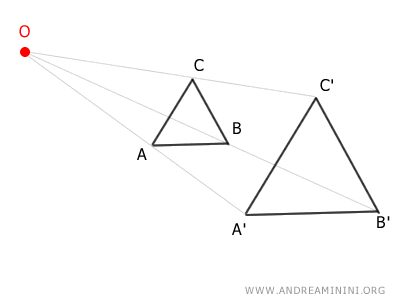
Il centro O è detto centro di omotetia mentre il fattore k è detto rapporto di omotetia.

L'omotetia diretta e inversa

L'omotetia può generare una riduzione o un ingrandimento della figura, mantenendo i punti sulla stessa retta (collinearità) e conservando le distanze relative tra i punti.

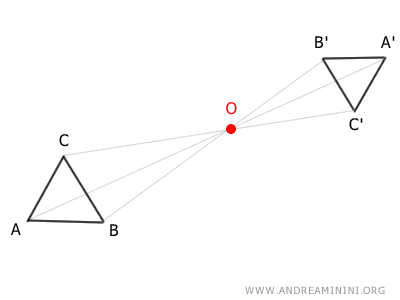
Ad esempio, considero una figura ABC e prendo il punto O come centro di omotetia e il numero k come rapporto di omotetia.

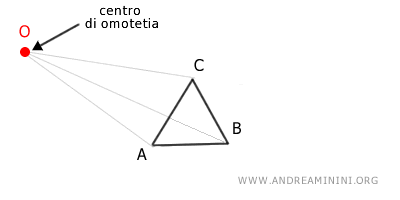
Considero il vettore $ \overrightarrow{OA} $ e lo moltiplico per il rapporto di omotetia k, ottenendo un altro vettore $ \overrightarrow{OA'} $ che ha la stessa origine e direzione del precedente (O) ma una lunghezza (modulo) differente.

$$ \overrightarrow{OA'} = k \times \overrightarrow{OA} $$

Questo mi permette di individuare un altro punto A' nel piano che si trova sulla stessa retta di OA.

 

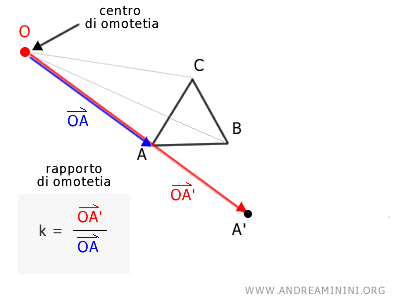
Quindi, se A è un punto della figura originale e A' è il suo corrispondente nella figura omotetica, allora i punti O, A, A' sono allineati e il segmento OA' è k volte il segmento OA

Nota. Sto usando dei vettori (es. $ \overrightarrow{OA} $) anziché dei segmenti (es. $ \overline{OA} $) perché nell'omotetia è importante considerare anche il verso della trasformazione geometrica, in quanto il rapporto di omotetia k può essere anche un numero negativo (k<0) ovvero una "omotetia inversa".

Se ripeto questo procedimento anche per gli altri punti B e C della figura iniziale, ottengo un altra figura A'B'C' che simile alla precedente.

La figura A'B'C' ha la stessa forma della figura ABC ma dimensioni diverse.

In questo caso la figura trasformata è ingrandita.

 

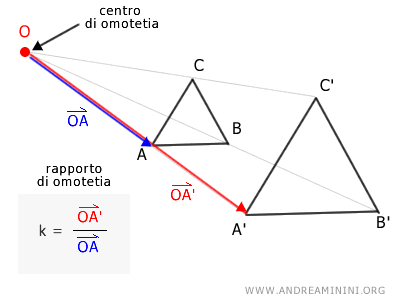
A seconda del rapporto di omotetia (k) possono verificarsi diversi effetti:

• Se |k| > 1 l'omotetia è una dilatazione
• Se |k| < 1 l'omotetia è una contrazione
• Se k = 1 l'omotetia è una identità e la figura resta la stessa.
• Se k = -1 l'omotetia equivale a una simmetria centrale.

E' importante ricordarsi che il rapporto di omotetia può anche essere negativo (k<0).

Il segno del rapporto di omotetia definisce il tipo di omotetia: diretta o inversa

• Omotetia diretta
  Se k>0 l'omotetia è detta omotetia diretta perché i punti corrispondenti si trovano sullo stesso quadrante
  
• Omotetia inversa
  Se k < 0 l'omotetia è detta omotetia inversa causa anche una riflessione rispetto al centro di omotetia O, oltre che una riduzione o un ingrandimento
  

A cosa serve? L'omotetia serve a ingrandire o ridurre figure geometriche mantenendo le proporzioni e le forme originali. E' molto utile quando si tratta di studiare le relazioni tra figure simili.

Un esempio pratico

Considero un quadrato di lato a e un centro di omotetia al suo centro O.

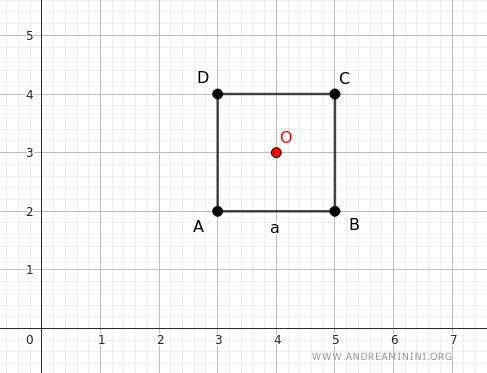
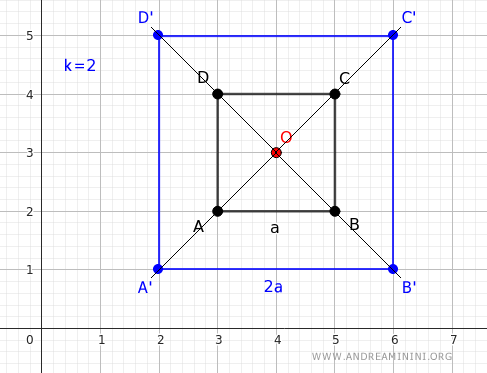
Se applico un'omotetia con rapporto k=2, ottengo un quadrato di lato 2a.

Il risultato è un ingrandimento.

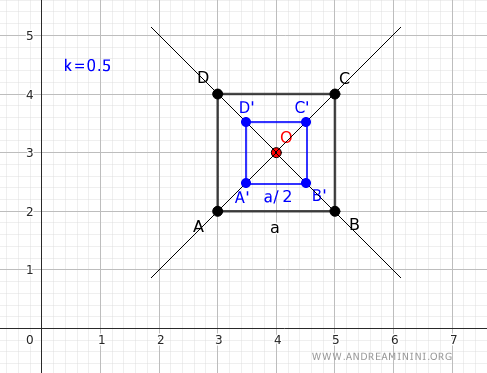
Se applico un'omotetia con rapporto k = 0.5, ottengo un quadrato di lato a/2

In questo caso il risultato è una riduzione

Ovviamente, a parità di fattore k il risultato cambia a seconda del punto di omotetia che scelgo.

Ad esempio, considero lo stesso quadrato ma con con un punto di omotetia O(2;3).

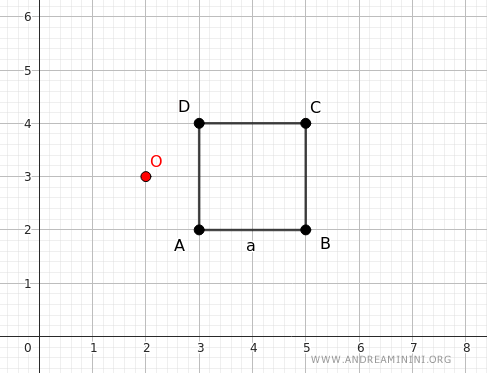
Se applico un'omotetia con rapporto k=2, ottengo un quadrato di lato 4a.

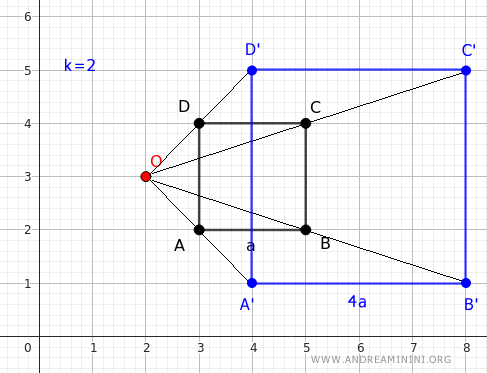
Il risultato è completamente diverso dal precedente.

Le equazioni di omotetia

Queste equazioni sono una rappresentazione semplificata dell'omotetia in coordinate cartesiane, quando il centro di omotetia è l'origine degli assi O(0;0) del piano cartesiano.

$$ \begin{cases} x′=k \cdot x \\ \\ y' = k \cdot y \end{cases} $$

Dove k è il rapporto di omotetia, (x,y) sono le coordinate di un punto della figura originale mentre (x′,y′) sono le coordinate del punto corrispondente nella figura omotetica.

Se il centro di omotetia O non fosse l'origine, ma un altro punto O(x₀,y₀) le equazioni sarebbero un po' più complesse.

$$ \begin{cases} x′=x_0 + k \cdot (x-x_0) \\ \\ y' = y_0 + k \cdot (y-y_0) \end{cases} $$

Queste equazioni descrivono come ogni punto della figura originale viene mappato nella figura omotetica rispetto al centro O(x₀,y₀).

Esempio. In questo esempio il rapporto di omotetia è k=2 e il centro di omotetia si trova alle coordinate O(2;3) quindi x₀=2 e y₀=3.

Il punto A si trova alle coordinate (x;y)=(3;2). Utilizzo le equazioni per calcolare le coordinate (x';y') del punto corrispondente A' dopo la trasformazione geometrica. $$ \begin{cases} x′=x_0 + k \cdot (x-x_0) \\ \\ y' = y_0 + k \cdot (y-y_0) \end{cases} $$ Applico il rapporto di omotetia k=2. $$ \begin{cases} x′=x_0 + 2 \cdot (x-x_0) \\ \\ y' = y_0 + 2 \cdot (y-y_0) \end{cases} $$ Sostituisco x₀=2 e y₀=3 $$ \begin{cases} x′=2 + 2 \cdot (x-2) \\ \\ y' = 3 + 2 \cdot (y-3) \end{cases} $$ Considero le coordinate del punto A ossia x=3 e y=2. $$ \begin{cases} x′=2 + 2 \cdot (3-2) \\ \\ y' = 3 + 2 \cdot (2-3) \end{cases} $$ $$ \begin{cases} x′=2 + 2 \cdot 1 \\ \\ y' = 3 + 2 \cdot (-1) \end{cases} $$ Quindi, le coordinate del punto corrispondente A' sono x'=4 e y'=1 $$ \begin{cases} x′=4 \\ \\ y' = 1 \end{cases} $$ Usando la stessa procedura posso calcolare gli altri punti corrispondenti B', C' e D'.

Omotetia nello spazio

L'omotetia nello spazio tridimensionale è una trasformazione geometrica che mantiene il rapporto tra le distanze rispetto a un punto fisso, detto centro di omotetia. Mi permette di scalare figure mantenendo le proporzioni.

Questa operazione è una generalizzazione dell'omotetia nel piano e si applica a tutti i punti di uno spazio tridimensionale.

 

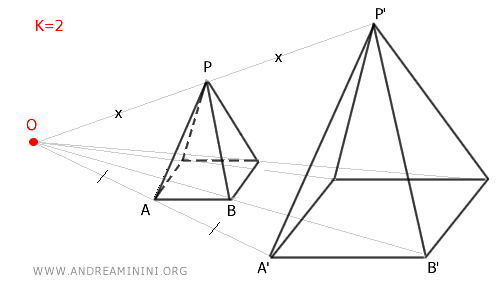
Sia \( O \) un punto fisso nello spazio e sia \( k \neq 0 \) un numero reale detto rapporto di omotetia.

L'omotetia con centro \( O \) e rapporto \( k \) trasforma ogni punto \( P(x, y, z) \) nel punto \( P'(x', y', z') \) secondo la relazione:

\[ P' = O + k (P - O) \]

In termini di coordinate, se \( O(x_0, y_0, z_0) \) e \( P(x, y, z) \), allora il punto trasformato \( P'(x', y', z') \) è dato da:

\[ x' = x_0 + k (x - x_0) \]

\[ y' = y_0 + k (y - y_0) \]

\[ z' = z_0 + k (z - z_0) \]

Questa formula significa che ogni punto \( P \) si sposta lungo la retta passante per \( O \) e \( P \), ridimensionandosi in base al valore di \( k \).

L'omotetia diretta e inversa

L'omotetia nello spazio tridimensionale può essere diretta o inversa a seconda del valore del rapporto \( k \).

• Omotetia diretta
  Se \( k > 0 \), l'omotetia è diretta: i punti si spostano radialmente rispetto al centro di omotetia, mantenendo lo stesso orientamento. I punti si allontanano o si avvicinano a \( O \), mantenendo l'orientamento. Se \( k>1 \) la figura solida viene ingrandita, viceversa se \( 0<k< 1 \) la figura viene ridotta. Ad esempio, per \( k=2 \) il solido raddoppia la sua dimensione. Nel caso in cui \( k=1 \) la trasformazione è identica, non cambia nulla.
  
• Omotetia inversa
  Se \( k < 0 \), l'omotetia è inversa: i punti vengono riflessi rispetto al centro \( O \) e si trovano dalla parte opposta della retta \( OP \). I punti si spostano dalla parte opposta rispetto a \( O \), invertendo l'orientamento. Nel caso particolare in cui \( k = -1 \) la figura solida viene ribaltata ma è congruente con l'originale perché mantiene le stesse distanze tra i punti e si ottiene lo stesso risultato di una simmetria centrale rispetto a \( O \).
  

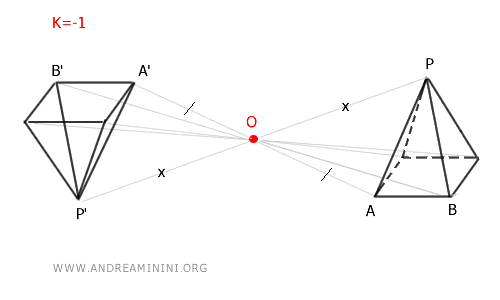
Esempio

Se applico un'omotetia diretta con \( k = 2 \) a un cubo centrato in \( O \), tutte le sue dimensioni raddoppiano, ma la forma e l'orientamento rimangono invariati.

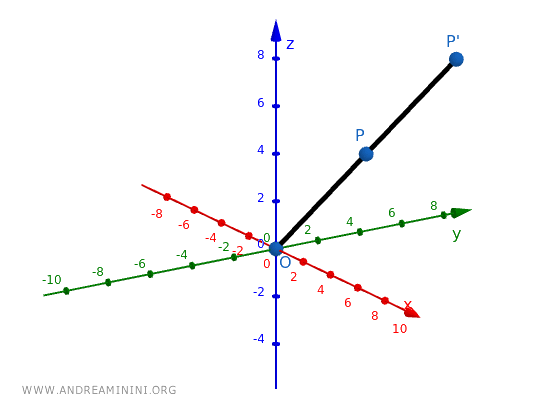
Supponiamo di avere un punto \( P(2, 3, 4) \) e di applicare un'omotetia di centro \( O(0,0,0) \) con \( k = 2 \):

\[ x' = 0 + 2(2 - 0) = 4 \]

\[ y' = 0 + 2(3 - 0) = 6 \]

\[ z' = 0 + 2(4 - 0) = 8 \]

Il nuovo punto è \( P'(4, 6, 8) \), che si trova sulla stessa direzione di \( P \) rispetto a \( O \), ma con una distanza doppia.

Esempio 2

Nel caso di una omotetia inversa l'oggetto trasformato si riflette rispetto a \( O \), invertendo l'orientamento. Se un omotetia con \( k = -1 \) viene applicata a un cubo, esso viene ribaltato rispetto al centro \( O \).

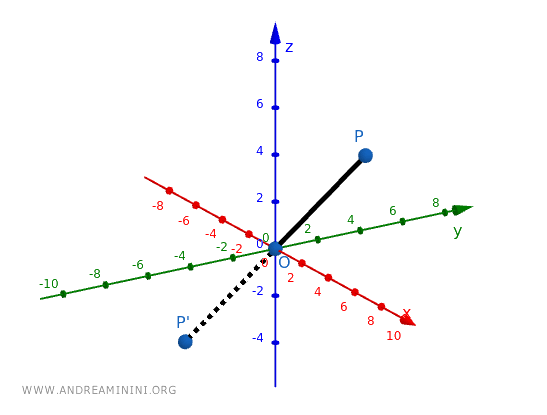
Se prendiamo lo stesso punto \( P(2, 3, 4) \) e applico un'omotetia con \( k = -1 \):

\[ x' = 0 + (-1)(2 - 0) = -2 \]

\[ y' = 0 + (-1)(3 - 0) = -3 \]

\[ z' = 0 + (-1)(4 - 0) = -4 \]

Il nuovo punto è \( P'(-2, -3, -4) \), che è il simmetrico di \( P \) rispetto al centro \( O \).

In altre parole, l'omotetia diretta conserva l'orientamento, mentre l'omotetia inversa inverte la disposizione dell'oggetto nello spazio.

Le proprietà dell'omotetia nello spazio

L'omotetia nello spazio tridimensionale ha le seguenti proprietà:

• Similitudine: Le figure omotetiche sono simili tra loro, mantenendo le proporzioni tra le distanze.
• Allineamento: Se tre punti erano allineati prima della trasformazione, lo saranno anche dopo.
• Parallelismo: Se due piani erano paralleli prima dell'omotetia, rimarranno paralleli dopo.
• Rapporti tra aree e volumi:
  - Se un oggetto ha area \( A \), dopo l'omotetia con rapporto \( k \), la nuova area sarà \( A' = k^2 A \).
  - Se un oggetto ha volume \( V \), dopo l'omotetia il volume sarà \( V' = k^3 V \).

Osservazioni

Alcune osservazioni e proprietà dell'omotetia

• L'omotetia non è una trasformazione isometrica
  Poiché le distanze assolute tra i punti cambiano, è evidente che, ad eccezione del caso k=1, l'omotetia non è una trasformazione isometrica. Tuttavia, come nelle isometrie, l'omotetia conserva alcune proprietà invarianti delle figure, come l'ampiezza degli angoli, la collinearità ossia l'allineamento dei punti, le proporzioni tra le distanze dei punti.
  
• Proporzionalità delle distanze
  Le distanze tra i punti nella figura omotetica sono proporzionali alle distanze corrispondenti nella figura originale. Quindi, le distanze relative tra i punti sono una proprietà invariante dell'omotetia (ma non le distanze assolute).
  
  

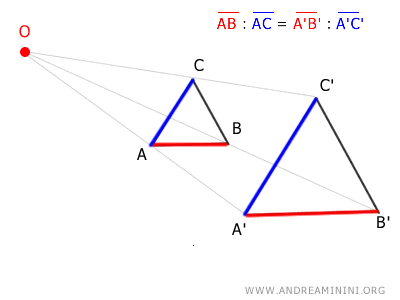
  Ad esempio, il segmento AB sta al segmento AC come il segmento A'B' sta al segmento A'C'. Vale la seguente proporzione: $$ \overline{AB}:\overline{AC} = \overline{A'B'}: \overline{A'C'} $$

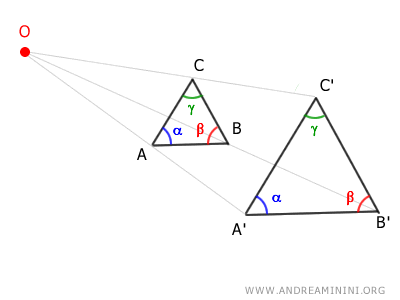
• Conservazione degli angoli
  Gli angoli nella figura originale e nella figura omotetica (la figura trasformata) sono congruenti ossia hanno la stessa ampiezza.
  
• Invarianza del centro
  Il centro di omotetia (O) rimane invariato dalla trasformazione ed è l'unico punto unito dell'omotetia.
  

  

• Se il rapporto di omotetia è k=-1, l'omotetia equivale alla simmetria centrale
  Quando il rapporto di omotetia è k=-1, i vettori della trasformazione hanno la stessa origine e direzione ma verso opposto. In questo caso particolare il risultato finale coincide con quello di una simmetria centrale nello stesso centro O.
  

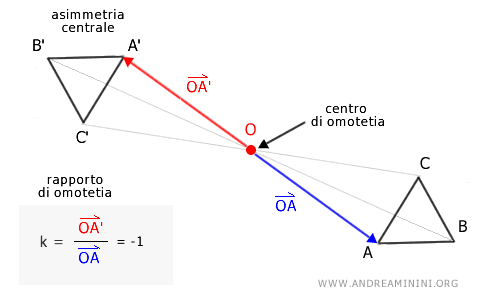
  Nota. In questo caso particolare i lati della figura originale e quelli corrispondenti della figura trasformata sono congruenti. $$ \overline{AB} \cong \overline{A'B'} \\  \overline{AC} \cong \overline{A'C'} \\ \overline{BC} \cong \overline{B'C'} $$

E così via