La distanza tra un punto e una retta con i vettori
La distanza minima di un punto P da una retta è il segmento PH perpendicolare alla retta che ha per estremi il punto P(x0;y0) e un punto H di intersezione sulla retta.
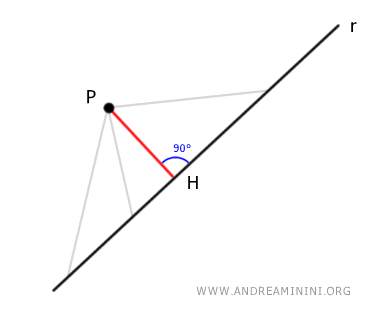
Per calcolare la distanza minima del segmento PH utilizzo la seguente formula. $$ D(P(x_0,y_0),r) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$
Un esempio pratico
Sul piano cartesiano ho una retta r
$$ 2x + 4y -6 = 0 $$
e un punto A
$$ A \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$
Rappresento sul piano cartesiano sia la retta che il punto
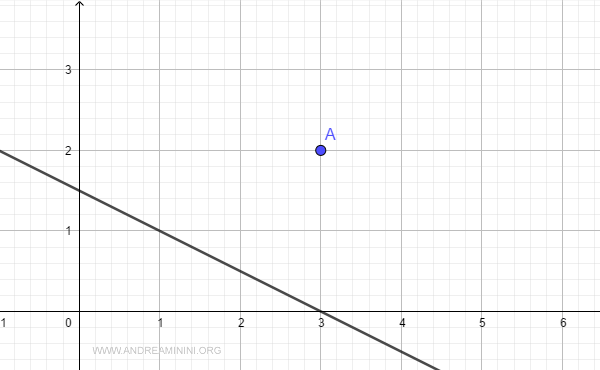
Qual è la distanza minima tra il punto e la retta?
Per trovare la distanza tra il punto A e la retta r applico la formula
$$ D(A(x_0,y_0),r) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$
Sostituisco le coordinate del punto A
$$ D(A(3,2),r) = \frac{|a(3)+b(2)+c|}{\sqrt{a^2+b^2}} $$
Sostituisco i coefficienti della retta
$$ D(A(3,2),r) = \frac{|2 \cdot (3)+4 \cdot (2)-6|}{\sqrt{2^2+4^2}} = \frac{|6+8-6|}{\sqrt{4+16}} = \frac{8}{\sqrt{20}} = 1.78 $$
Quindi la distanza minima tra il punto A e la retta è 1,78.
Qual è il punto della retta più vicino al punto?
Conosco la distanza minima tra il punto A e la retta.
Ora voglio conoscere qual è il punto della retta più vicino al punto A.
La distanza minima deve trovarsi su una retta perpendicolare r' che passi per il punto A.
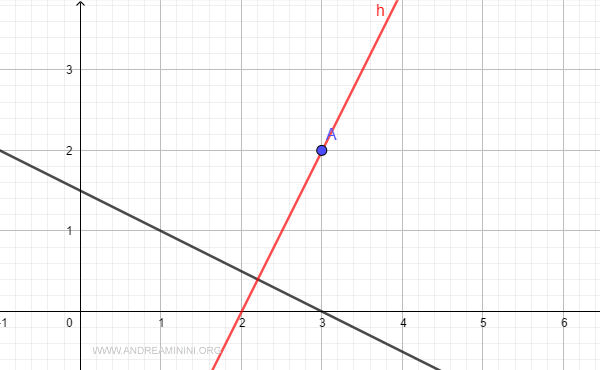
L'equazione vettoriale della retta perpendicolare r' è la seguente:
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
Nota. Le coordinate (3,2) sono il punto A mentre il vettore (2,4) è il vettore normale ossia il vettore perpendicolare al vettore direttore della retta..
Trasformo l'equazione vettoriale in parametrica
$$ \begin{cases} x = 3 + 2 t \\ y = 2 + 4t \end{cases} $$
Il punto della retta più vicino al punto A deve trovarsi in questa retta.
Aggiungo l'equazione della retta r come ulteriore condizione del sistema.
$$ \begin{cases} x = 3 + 2 t \\ y = 2 + 4t \\ 2x + 4y -6 = 0 \end{cases} $$
Poi risolvo il sistema per t
$$ \begin{cases} x = 3 + 2 t \\ y = 2 + 4t \\ 2(3+2t) + 4(2+4t) -6 = 0 \end{cases} $$
$$ \begin{cases} x = 3 + 2 t \\ y = 2 + 4t \\ 6+4t + 8+16t -6 = 0 \end{cases} $$
$$ \begin{cases} x = 3 + 2 t \\ y = 2 + 4t \\ 8+20t = 0 \end{cases} $$
$$ \begin{cases} x = 3 + 2 t \\ y = 2 + 4t \\ 8+20t = \frac{-8}{20}= \frac{-2}{5} \end{cases} $$
Ho trovato il parametro t della retta perpendicolare r'.
A questo punto, per trovare le coordinate del punto H sulla retta più vicino al punto A, mi basta sostituire il parametro t nelle equazioni parametriche con il valore appena trovato.
$$ \begin{cases} x = 3 + 2 t \\ y = 2 + 4t \end{cases} $$
$$ \begin{cases} x = 3 + 2 \cdot \frac{-2}{5} \\ y = 2 + 4 \cdot \frac{-2}{5} \end{cases} $$
$$ \begin{cases} x = \frac{15-4}{5} \\ y = \frac{10-8}{5} \end{cases} $$
$$ \begin{cases} x = \frac{11}{5} = 2.2 \\ y = \frac{2}{5} = 0.4 \end{cases} $$
Ho così trovato le coordinate del punto H sulla retta.
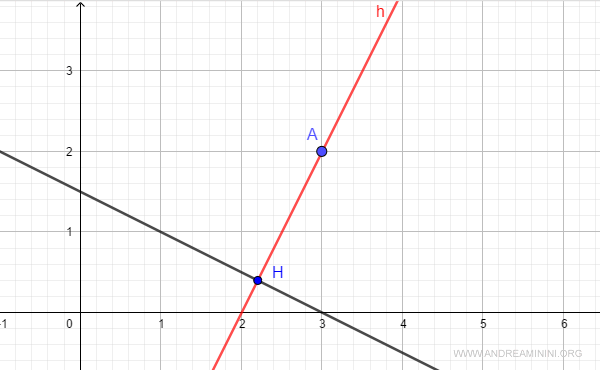
Nota. Per una verifica provo a calcolare la distanza tra i due punti AH. Se tutto è corretto dovrei ottenere la stessa distanza tra il punto A e la retta r. $$ || A-H || = || \begin{pmatrix} 3 - \frac{11}{5} \\ 2 - \frac{2}{5} \end{pmatrix} || = || \begin{pmatrix} \frac{4}{5} \\ \frac{8}{5} \end{pmatrix} || = $$ $$ || A-H || = \sqrt{(\frac{4}{5})^2+(\frac{8}{5})^2} = \sqrt{(\frac{16}{25})+(\frac{64}{25})} = \sqrt{\frac{16}{5}} = 1.78 $$ Tutto ok. E' la stessa distanza.
E così via.
