Quadrato

Un quadrato è un parallelogramma con quattro lati congruenti e quattro angoli retti.

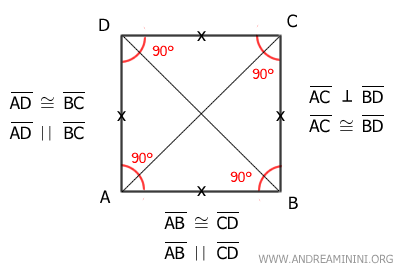
In alternativa, si può dire anche che un quadrato è un parallelogramma con quattro lati e quattro angoli congruenti. Quindi, il quadrato è sia un rombo che un rettangolo.

Eredita tutte le proprietà del rombo:

• I lati del rombo sono congruenti
• Le diagonali sono perpendicolari, ossia formano un angolo di 90°
• Le diagonali sono le bisettrici degli angoli

Inoltre, eredita tutte le proprietà del rettangolo:

• ogni angolo del rettangolo è un angolo retto (90°)
• le diagonali sono congruenti, ossia hanno la stessa lunghezza

Le formule

Le principali formule del quadrato

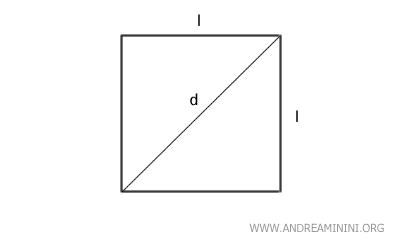
• Il perimetro
  Il perimetro del quadrato è uguale a quattro volte la lunghezza di un lato (l) $$ P = 4 \cdot l = l + l + l + l $$
• L'area
  L'area del quadrato è uguale al lato al quadrato (l²) $$ A = l^2 $$ In alternativa, l'area del quadrato è uguale alla diagonale (d) al quadrato diviso due. $$ A=\frac{d^2}{2} $$
• La diagonale
  La diagonale del quadrato è al prodotto tra il lato e la radice quadrata di 2 $$ d = l \cdot \sqrt{2} $$

  Nota. Quest'ultima formula deriva dal teorema di Pitagora. La diagonale è l'ipotenusa di un triangolo rettangolo in cui i cateti sono due lati del quadrato $$ d = \sqrt{l^2+l^2} $$ $$ d = \sqrt{2 \cdot l^2} $$ Faccio uscire il lato dalla radice quadrata e ottengo la formula precedente $$ d = l \cdot \sqrt{2} $$
  

• Il lato
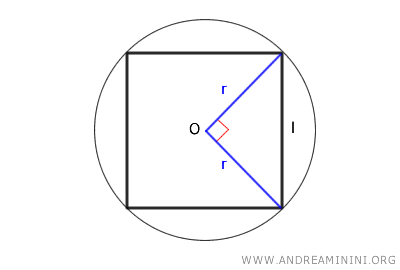
  Il lato del quadrato si può ottenere semplicemente dividendo il perimetro per quattro $$ l = \frac{p}{4} $$ oppure tramite la radice quadrata dell'area $$ l = \sqrt{A} $$ La misura del lato si può ottenere anche tramite la relazione tra il lato e il raggio del cerchio circoscritto al quadrato, moltiplicando il raggio per la radice quadrata di due. $$ l = r \cdot \sqrt{2} $$

  Nota. Anche quest'ultima formula deriva dal teorema di Pitagora. I raggi tra il centro del cerchio (O) e due estremi di un lato del quadrato (l) formano un angolo di 90°. Viene così a crearsi un triangolo rettangolo in cui i cateti hanno la misura del raggio e l'ipotenusa quella del lato del quadrato.  $$ l = \sqrt{r^2+r^2} $$ $$ l = \sqrt{2r^2} $$  Faccio uscire il raggio dalla radice e ottengo la formula che cercavo. $$ l = r \cdot \sqrt{2} $$
  

• Il lato del quadrato è il doppio del raggio del cerchio inscritto al quadrato. $$ l = 2r $$

  Nota. Questa formula è abbastanza intuitiva. Il doppio del raggio 2r (il diametro) del cerchio inscritto è congruente con i lati del quadrato. Questo avviene perché il diametro del cerchio inscritto tocca esattamente i lati del quadrato in quattro punti di tangenza (uno per lato), rendendo il cerchio il più grande possibile che può essere contenuto all'interno del quadrato senza oltrpassare i suoi lati.
  
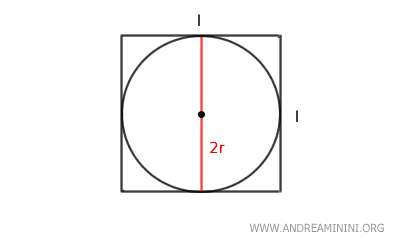
  Si può anche dimostrare che esiste una relazione tra il raggio del cerchio inscritto e il lato del quadrato.

Come disegnare un quadrato

Traccio il segmento AB come primo lato del quadrato.

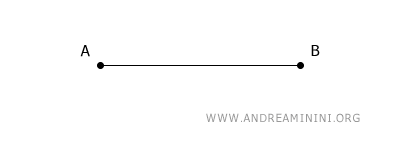
Centro il compasso sull'estremo A e traccio un arco con apertura a piacere.

L'arco interseca il segmento AB nel punto C.

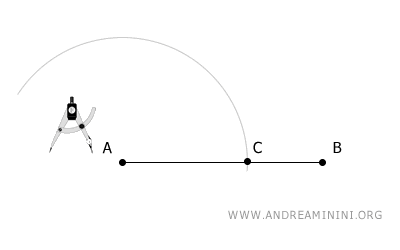
Con la stessa apertura (raggio), centro il compasso nel punto C e disegno un secondo arco che interseca il primo arco nel punto D.

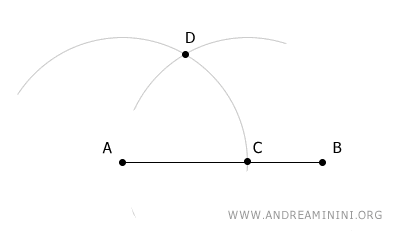
Ora centro il compasso nel punto D con la stessa apertura e traccio un terzo arco che interseca il primo arco nel punto E.

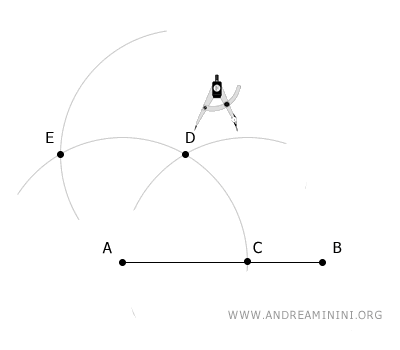
Infine, centro il compasso nel punto E e con lo stesso raggio traccio un arco che interseca l'ultimo arco nel punto F.

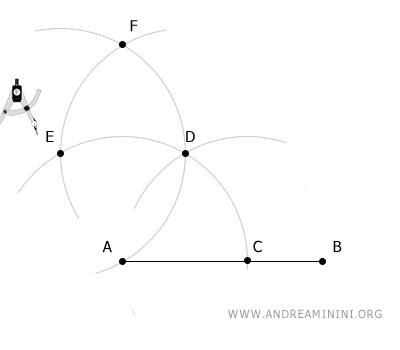
A questo punto, disegno una retta tra i punti A e F.

In questo modo ho trovato la retta perpendicolare alla retta AB che passa per il punto A.

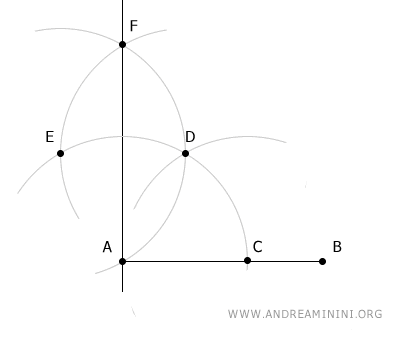
Centro il compasso sul punto A e con un raggio pari ad AB traccio un arco che interseca la retta perpendicolare nel punto F.

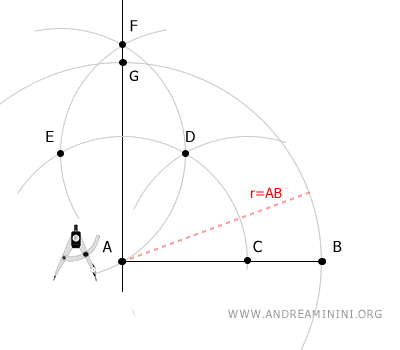
Mantenendo la stessa apertura, centro il compasso sul punto G e traccio un altro arco.

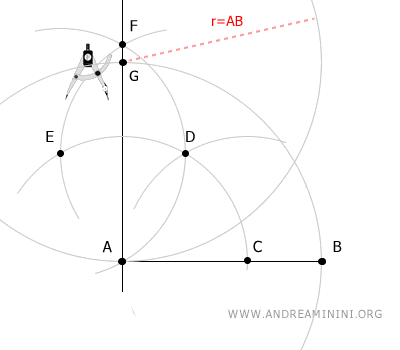
Infine, con la stessa apertura, centro il compasso sul punto B e traccio un arco che interseca l'ultimo nel punto H.

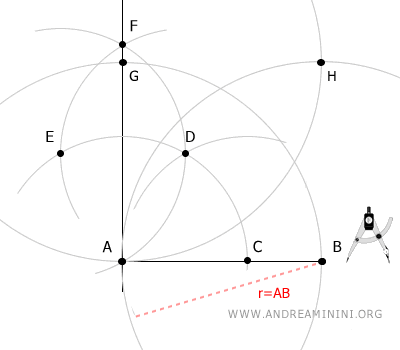
Traccio dei segmenti tra i punti AB, AG, GH, BH.

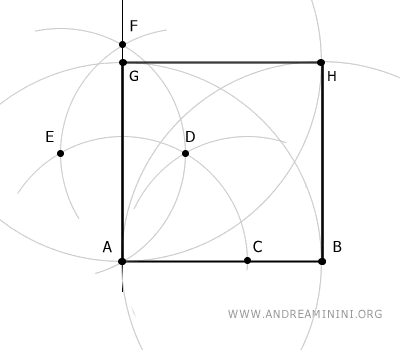
La figura finaleABHG è un quadrato.

In alternativa, posso anche disegnare il quadrato inscritto in una circonferenza.

Osservazioni

Alcune osservazioni e note sui quadrati

• Un quadrato ha le diagonali congruenti

  Dimostrazione. Un quadrato ABCD ha, per definizione, tutti i lati congruenti e tutti gli angoli congruenti (angoli retti). Partendo da queste ipotesi posso affermare che i triangoli ABD e ABC sono congruenti per il primo principio di congruenza (criterio del lato-angolo-lato, o LAL) perché hanno un lato coincidente (AC), i lati congruenti (AB≅BC) e l'angolo compreso tra questi lati congruente (90°), ovvero l'angolo retto.
  
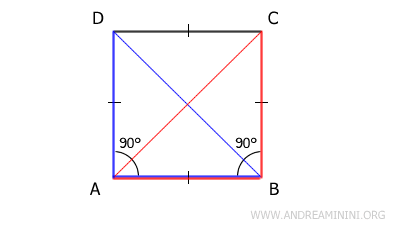
  I triangoli ABD≅ABC congruenti hanno tutti i lati e angoli congruenti nello stesso ordine. In particolare, mi interessa sapere che le loro ipotenuse AC e BD sono congruenti (AC≅BD) perché sono anche le diagonali del quadrato. In conclusione, la tesi è dimostrata: le diagonali del quadrato sono congruenti.

• Un parallelogramma è un quadrato se ha le diagonali congruenti e perpendicolari

  Dimostrazione. Per l'ipotesi iniziali il parallelogramma ABCD ha le diagonali congruenti AC≅BD e perpendicolari tra loro. Essendo un parallelogramma, le diagonali si incontrano nel loro punto medio M. Quindi le semidiagonali AM, BM, CM, DM sono congruenti tra loro.
  
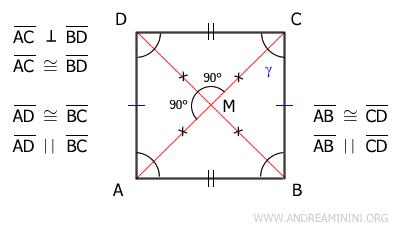
  Da questo deduco che i triangoli AMD e CDM sono congruenti per il primo principio di congruenza (LAL) perché hanno un lato coincidente DM, i lati AM≅CM congruenti e l'angolo compreso congruente (90°). Quindi, i triangoli AMD≅CDM hanno tutti i lati e gli angoli congruenti.
  
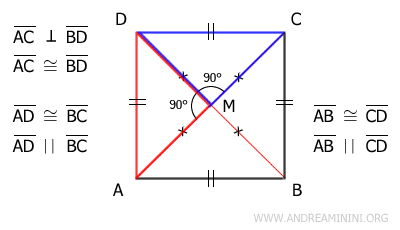
  In questo caso mi interessa sapere soprattutto che le loro ipotenuse AD≅CD sono congruenti, perché AC e CD sono anche due lati continui del parallelogramma. In un parallelogramma i lati opposti sono congruenti. Da questo deduco che tutti i lati del parallelogramma sono congruenti ossia hanno la stessa lunghezza. Inoltre, sapendo per l'ipotesi iniziale che le diagonali sono congruenti, deduco che si tratta di un quadrato e non di un rombo.

• Una diagonale divide il quadrato in due triangoli rettangoli isosceli

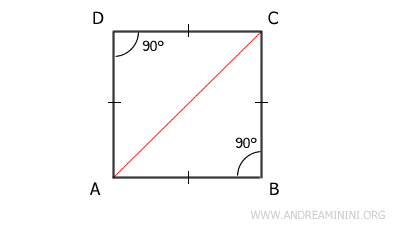
  Dimostrazione. Per definizione un quadrato ABCD ha i lati congruenti e gli angoli congruenti (angoli retti). Una diagonale, ad esempio AC, divide il quadrato in due triangoli rettangoli perché uno degli angoli è sicuramente un angolo retto (90°). I due triangoli sono anche isosceli perché due loro lati (AB≅BC e AD≅CD) sono sicuramente congruenti per l'ipotesi iniziale.
  
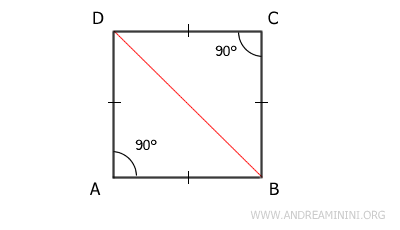
  Lo stesso risultato si ottiene analizzando l'altra diagonale BD del quadrato. Anche in questo caso, per le stesse ragioni, la diagonale divide il quadrato in due triangoli rettangoli isosceli.
  

• Le due diagonali dividono il quadrato in quattro triangoli isosceli

  Dimostrazione. Il quadrato ABCD è un parallelogramma con tutti i lati e angoli congruenti. Tutti i parallelogrammi hanno le diagonali che si incontrano nel loro punto medio M.
  
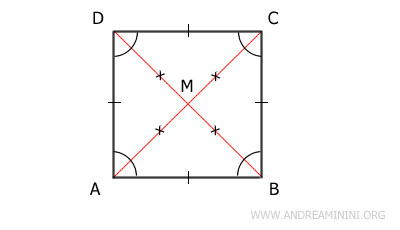
  A differenza di altri parallelogrammi, in un quadrato le diagonali sono anche congruenti tra loro. Questo vuol dire che il quadrato può essere scomposto in quattro triangoli con due lati obliqui congruenti, ovvero in quattro triangoli isosceli ABM, BCM, CDM, ADM. Poiché in un quadrato le diagonali sono anche perpendicolari fra loro, i quattro triangoli sono anche triangoli rettangolo oltre a essere isosceli.

• Un parallelogramma è un quadrato se le diagonali sono congruenti e una diagonale è una bisettrice di un angolo

  Dimostrazione. Per ipotesi nel parallelogramma ABCD le diagonali AC≅BD sono congruenti. Inoltre, una diagonale è bisettrice di un angolo. Ad esempio, la diagonale AC è bisettrice dell'angolo al vertice A. Quindi, gli angoli α' e α'' sono congruenti (α'≅α'').
  
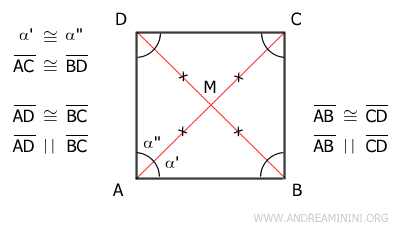
  Essendo un parallelogramma, i lati opposti sono congruenti (AB≅CD e AD≅BC) e paralleli (AB||CD e AD||BC). Quindi la diagonale AC posso considerarla come la trasversale tra due rette parallele AD e BC. Di conseguenza, per il teorema delle rette parallele, gli angoli alterni interni α''≅γ sono congruenti.
  
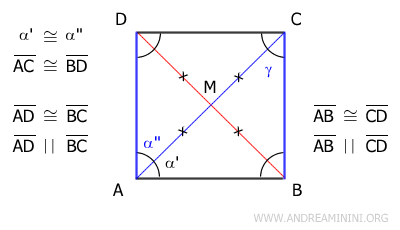
  Poiché α'≅α'' sono congruenti per l'ipotesi iniziale, deduco che anche α'≅γ sono congruenti. Questo vuol dire che il triangolo ABC è un triangolo isoscele, perché ha due angoli congruenti alla base AC. Essendo un triangolo isoscele, i suoi due lati obliqui AB≅BC sono congruenti. Di conseguenza, essendo due lati consecutivi del parallelogramma, posso affermare che tutti i lati del parallelogramma sono congruenti.
  
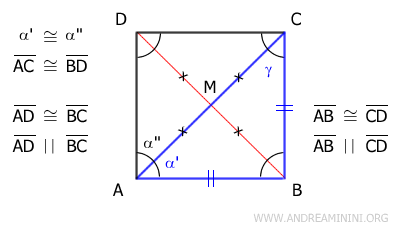
  Resta ancora da capire se il parallelogramma è un rombo o un quadrato. Quest'ultimo quesito è di facile soluzione. Sapendo per l'ipotesi iniziale che le diagonali sono congruenti, deduco che la figura geometrica ABCD è un quadrato.

E così via