I segmenti

Un segmento è una parte di una retta delimitata da due punti A e B chiamati estremi.

I punti estremi A e B determinano i limiti del segmento e sono inclusi nel segmento stesso.

Il segmento è quindi rappresentato da una linea retta che inizia da un punto e si estende fino a raggiungere l'altro punto.

Tutti i punti tra gli estremi sono detti punti interni del segmento.

Nota. Pur essendo una retta delimitata, il segmento è composto da infiniti punti perché, dati due punti diversi qualsiasi del segmento, è sempre possibile trovare un punto intermedio tra questi. In altre parole, il segmento è un insieme denso. Fa eccezione alla regola solo il segmento nullo. Quando gli estremi del segmento coincidono, il segmento è detto segmento nullo. Nel caso particolare del segmento nullo, il segmento è composto da un solo punto.

Un segmento può essere considerato come una parte della retta.

Le semirette che appartengono alla stessa retta "r" del segmento e hanno origine da un estremo del segmento, senza passare per l'altro estremo, sono detti prolungamenti del segmento.

Due segmenti sono detti segmenti consecutivi se hanno in comune uno e un solo estremo.

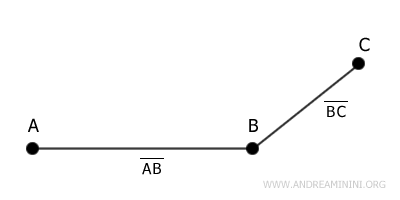
Due segmenti sono detti segmenti adiacenti se sono consecutivi e appartengono alla stessa retta.

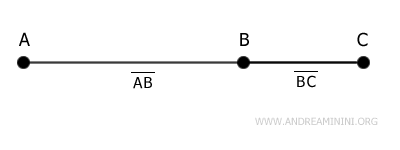
Ogni segmento ha una lunghezza definita, che corrisponde alla distanza tra i suoi estremi e può essere misurata tramite un'unità di misura, come centimetri, metri o altre unità di lunghezza.

Nota. I segmenti sono utilizzati nella geometria per costruire figure più complesse. Sono importanti anche nel calcolo vettoriale, perché rappresentano la lunghezza del vettore che collega due punti.

I segmenti che hanno la stessa lunghezza sono segmenti congruenti e, indipendentemente dalla loro posizione nello spazio, appartengono alla stessa classe.

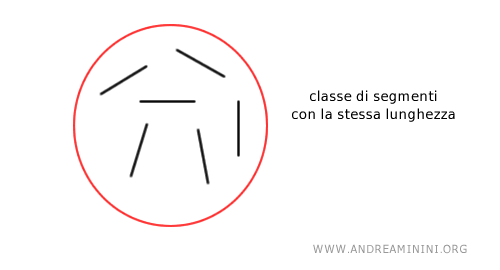
Nota. La "congruenza" è un termine che si usa in geometria quando due oggetti hanno la stessa forma e dimensione ma occupano una diversa posizione nello spazio. Nel caso di segmenti, se due segmenti sono congruenti, significa che hanno la stessa lunghezza.

Pertanto la lunghezza è una classe di equivalenza che accomuna più segmenti.

Si distingue dalla misura della lunghezza che, invece, è semplicemente un numero. Ad esempio, un segmento è lungo 3 cm.

E così via.