L'equazione cartesiana della sfera

Una sfera è un insieme di punti P dello spazio R3 equidistanti da un punto centrale C detto centro della sfera. La distanza tra i punti e il centro è detta raggio r. $$ d(C,P)=r $$

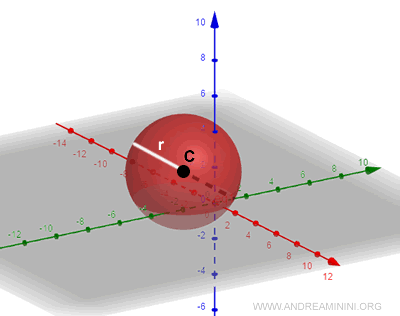
• Punti interni
  I punti con distanza compresa tra 0 e r sono detti punti interni della sfera. $$ 0 < d(C,P) < r $$
• Punti esterni
  I punti con distanza d(C,P) > r sono detti punti esterni della sfera. $$ d(C,P) > r $$

Nota. Se la distanza è nulla la sfera degenera in un solo punto C.

Come trovare l'equazione cartesiana della sfera

La definizione della sfera mi permette di costruire l'equazione cartesiana della sfera.

$$ d(C,P)=r $$

Fisso un riferimento cartesiano RC(O;i,j,k)

Il centro C è un punto caratterizzato da coordinate x,y,z nello spazio euclideo.

$$ C = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} $$

Poi prendo un generico punto P della sfera

$$ P = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$

A questo punto calcolo la distanza tra i due punti

$$ d(C,P) = \sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2} $$

Sapendo che la distanza d(C,P) eguaglia il raggio r

$$ d(C,P) = r $$

Posso scrivere

$$ \sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2} = r $$

Elevo entrambi i membri alla seconda

$$ \begin{pmatrix} \sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2} \end{pmatrix} ^2 = (r)^2 $$

$$ (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2 $$

Ho così trovato l'equazione cartesiana in forma canonica della sfera.

$$ (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2 $$

Ogni sfera ha una propria equazione canonica ed è unica.

Per trovare l'equazione cartesiana della sfera svolgo i calcoli algebrici sull'equazione canonica.

$$ (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2 $$

$$ (x^2-2xx_0+x_0^2)+(y^-2yy_0+y_0^2)+(z^2-2zz_0+z_0^2) = r^2 $$

$$ x^2-2xx_0+x_0^2 + y-2yy_0+y_0^2 + z^2-2zz_0+z_0^2 - r^2 = 0 $$

A questo punto raccolgo i coefficienti in questo modo

$$ \begin{pmatrix} a=-2x_0 \\ b = -2y_0 \\ c = -2z_0 \\ d=x_0^2+y_0^2+z_0^2-r^2 \end{pmatrix} $$

Nota. In alcuni casi il precedente sistema è utile anche per determinare il raggio e il valore delle incognite a partire dai coefficienti. Dopo semplici passaggi algebrici diventa $$ \begin{pmatrix} x_0= - \frac{a}{2} \\ y_0 = - \frac{b}{2} \\ z_0 = - \frac{c}{2} \\ r=\sqrt{x_0^2+y_0^2+z_0^2-d} \end{pmatrix} $$ L'espressione sotto radice deve essere non negativa. Quindi la condizione necessaria che si tratti di una sfera è $$ x_0^2+y_0^2+z_0^2-d \ge 0 $$ o in alternativa sostituendo le incognite con i coefficienti $$ (\frac{a}{2})^2 + (\frac{b}{2})^2 + (\frac{c}{2})^2 - d \ge 0 $$.

Poi sostituisco i coefficienti all'equazione precedente e ottengo l'equazione cartesiana della sfera.

$$ x^2 + y^2 + z^2 + ax + by + cz + d = 0 $$

Come già anticipato, ogni sfera ha una propria equazione cartesiana ed è unica.

Un esempio pratico

Devo determinare se questa equazione cartesiana è una sfera oppure no

$$ x^2 + y^2 + z^2 + 3x + 2y -3z - 4 = 0 $$

I coefficienti sono

$$ \begin{pmatrix} a=3 \\ b = 2 \\ c=-3 \\ d=-4 \end{pmatrix} $$

E' una sfera se

$$ (\frac{a}{2})^2 + (\frac{b}{2})^2 + (\frac{c}{2})^2 - d \ge 0 $$

$$ (\frac{3}{2})^2 + (\frac{2}{2})^2 + (\frac{-3}{2})^2 - (-4) \ge 0 $$

$$ \frac{9}{4} + 1 + \frac{9}{4} +4 \ge 0 $$

$$ \frac{9}{2} + 5 \ge 0 $$

$$ \frac{19}{2} \ge 0 $$

L'espressione è non negativa. Pertanto, si tratta di una sfera.

Come trovare il centro e il raggio della sfera

Una volta appurato che si tratta di una sfera, posso calcolare le coordinate del centro C ( x₀,y₀,z₀ ) e del raggio r.

$$ \begin{pmatrix} a=-2x_0 \\ b = -2y_0 \\ c = -2z_0 \\ d=x_0^2+y_0^2+z_0^2-r^2 \end{pmatrix} $$

$$ \begin{pmatrix} 3=-2x_0 \\ 2 = -2y_0 \\ -3 = -2z_0 \\ -4=x_0^2+y_0^2+z_0^2-r^2 \end{pmatrix} $$

$$ \begin{pmatrix} x_0 = - \frac{3}{2} \\ y_0 = -\frac{2}{2} = -1 \\ z_0 = \frac{3}{2} \\ r^2=x_0^2+y_0^2+z_0^2+4 \end{pmatrix} $$

$$ \begin{pmatrix} x_0 = - \frac{3}{2} \\ y_0 = -1 \\ z_0 = \frac{3}{2} \\ r= \sqrt{ (- \frac{3}{2})^2+(-1)^2+( \frac{3}{2})^2+4 } \end{pmatrix} $$

$$ \begin{pmatrix} x_0 = - \frac{3}{2} \\ y_0 = -1 \\ z_0 = \frac{3}{2} \\ r= \sqrt{ \frac{9}{4}+1+ \frac{9}{4}+4 } \end{pmatrix} $$

$$ \begin{pmatrix} x_0 = - \frac{3}{2} \\ y_0 = -1 \\ z_0 = \frac{3}{2} \\ r= \sqrt{ \frac{9}{2}+5 } \end{pmatrix} $$

$$ \begin{pmatrix} x_0 = - \frac{3}{2} \\ y_0 = -1 \\ z_0 = \frac{3}{2} \\ r= \sqrt{ \frac{19}{2} } \approx 3.08 \end{pmatrix} $$

Ho così trovato le coordinate del punto centrale C

$$ C = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} = \begin{pmatrix} - \frac{3}{2} \\ -1 \\ \frac{3}{2} \end{pmatrix} $$

e il valore del raggio r

$$ r = 3.08 $$

E così via.

Nota. Ho verificato su Geogebra le coordinate del punto centrale C e la misura del raggio della sfera. I calcoli sono corretti.

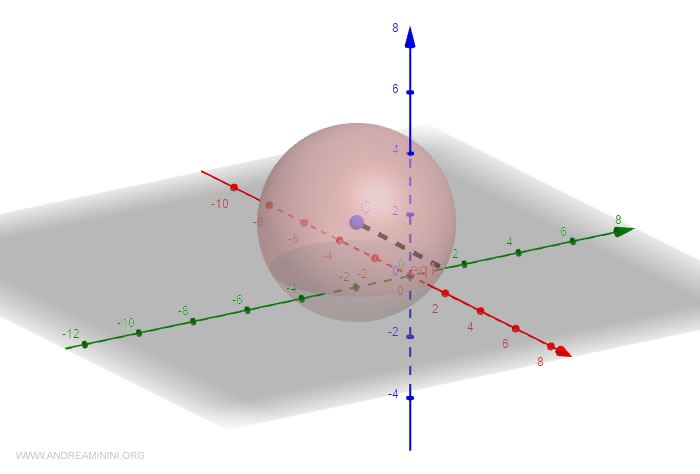
E così via.