Rette

Cos'è una retta

Una retta è un insieme ordinato di punti che si estende in entrambe le direzioni all'infinito senza curvarsi mai.

La retta è un oggetto geometrico fondamentale della geometria euclidea.

In base al primo postulato di Euclide, tra due punti diversi dello spazio In base passa una e una sola retta.

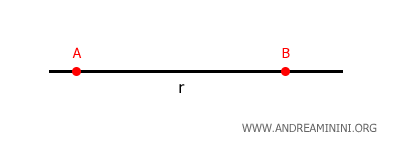
In genere per indicare le rette si utilizzano le lettere minuscole mentre per indicare i punti le lettere maiuscole.

Nota. Da questo deduco che la retta non possa mai curvare, perché prendendo due coppie di punti del piano (A,B) e (B,C) diversi tra loro, questi appartengono a un'unica retta soltanto se sono tutti allineati.

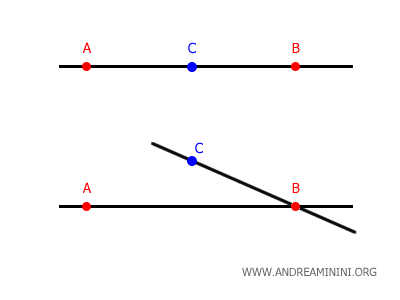
In base al secondo postulato di Euclide, una retta è un segmento che può essere esteso all'infinito in entrambe le direzioni.

Quindi, in una retta non esiste né un primo punto, né un ultimo punto.

Nota. Questo distingue una retta da un segmento che, invece, è dotato di due estremità ossia di un punto iniziale e finale.

Dati due punti qualsiasi della retta, esiste sempre almeno un altro punto tra di essi.

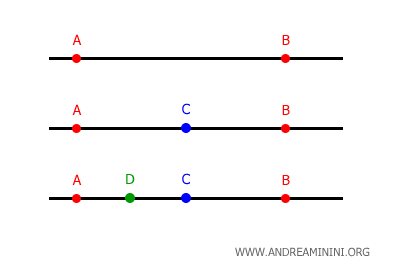
Per questa ragione si dice che la retta è un insieme denso.

Nota. Esiste una corrispondenza biunivoca tra i punti della retta e l'insieme dei numeri reali. Entrambi sono insiemi con infiniti elementi della stessa densità.

Dai primi due postulati di Euclide derivano diverse proprietà della retta.

Quando due o più rette passano per lo stesso punto sono dette rette incidenti o rette concorrenti.

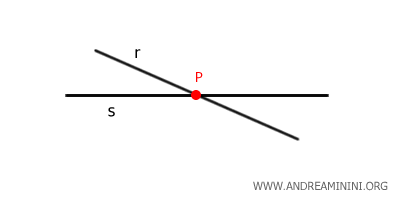
In un punto passano infinite rette.

L'insieme delle rette passanti per un punto è detto fascio proprio di rette.

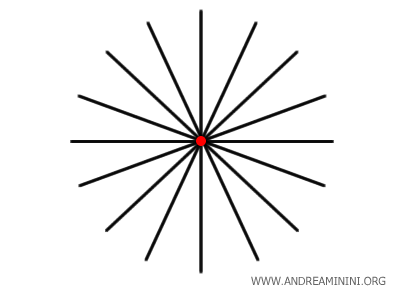
Nota. Sapendo che una retta è un insieme di punti, deduco che una retta contiene almeno un punto. Per definire una retta servono almeno due punti, quindi deduco che in un punto qualsiasi passano infinite rette.

Ogni piano contiene infiniti punti, quindi contiene infinite rette.

Per definire un piano sono necessari almeno tre punti non allineati.

Nello spazio a tre dimensioni una retta può essere definita come l'intersezione di due piani.

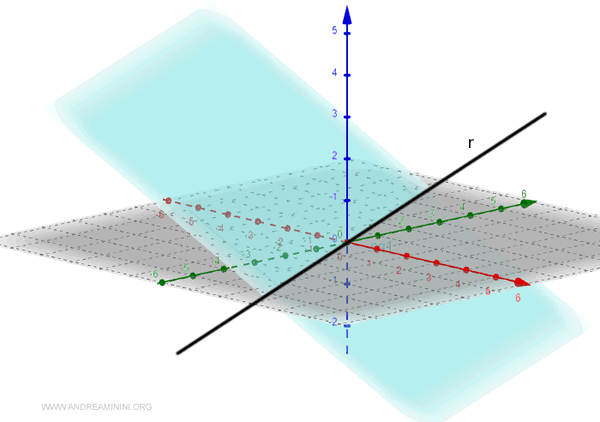
Nota. Questo concetto è una semplificazione di un concetto molto più generale che può essere esteso a molte più dimensioni nella matematica avanzata.

In una retta è sempre possibile fissare un verso di percorrenza.

Una retta in cui sia fissato un verso è detta retta orientata.

Nel piano cartesiano, una retta può essere definita tramite l'equazione lineare

$$ y = mx + b $$

Dove

• "y" è il valore della coordinata verticale di ogni punto sulla retta
• "x" è il valore della coordinata orizzontale di ogni punto sulla retta
• "m" è il coefficiente angolare della retta, cioè rappresenta la pendenza della retta, ossia m=y/x
• "b" è l'intercetta, cioè il punto in cui la retta interseca l'asse y (quando x = 0).

Graficamente l'equazione della retta sul piano cartesiano si rappresenta in questo modo

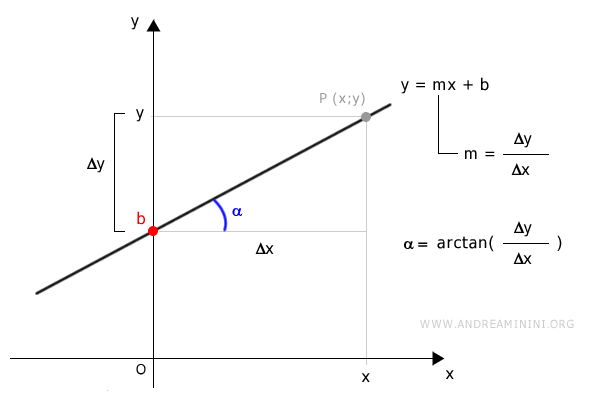
Dati due punti qualsiasi della retta, è sempre possibile trovare l'equazione della retta utilizzando la formula per la pendenza e l'equazione della retta stessa.

E così via.