Lunghezza
La lunghezza è la dimensione di un oggetto che indica la sua estensione nello spazio. Ad esempio, la lunghezza di un segmento.
La lunghezza è una delle grandezze fisiche fondamentali, perché non è definita a partire da altre grandezze fisiche.
L'unità di misura della lunghezza nel Sistema Internazionale è il metro e i vari multipli (es. chilometro) e sottomultipli (es. centrimetro, millimetro, ecc.).
Secondo la definizione attuale, un metro è la distanza percorsa dalla luce nel vuoto in un intervallo di tempo pari a 1/299792458 di secondo.
Nota. La storia della misurazione della lunghezza risale alle civiltà antiche perché ha infinite applicazioni pratiche (es. costruzione di edifici, la distanza delle tratte commerciali, ecc. ). Nell'antichità venivano utilizzate unità di misura basate su parti del corpo umano, come il piede o il braccio. Ad esempio, il cubito egiziano era la distanza tra la mano e il gomito, ecc. Con il progresso tecnico-scientifico queste misure sono state standardizzate per facilitare il commercio e la comunicazione scientifica.
Il significato della lunghezza
La lunghezza è una delle grandezze più fondamentali nella comprensione e nella manipolazione del nostro mondo.
Ad esempio, spesso basta un colpo d'occhio per capire se un bastoncino è più corto o più lungo di un altro.

Tuttavia, la semplicità apparente della "lunghezza" nasconde una profonda complessità, perché questo termine può assumere diversi significati a seconda del contesto, del campo di studio o della disciplina tecnica o scientifica.
Ad esempio, nella geometria euclidea la lunghezza di un segmento è semplicemente la distanza tra i due punti estremi del segmento.

Due segmenti sono detti segmenti congruenti se hanno la stessa lunghezza, ovvero se possono essere sovrapposti tra loro occupando gli stessi punti del piano.
In questi casi si dice che i due segmenti congruenti appartengono alla stessa classe di equivalenza.
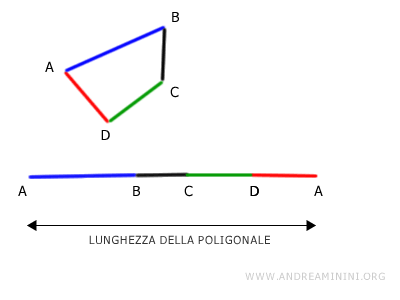
La lunghezza di una poligonale è, invece, la somma delle lunghezze dei segmenti che la compongono.
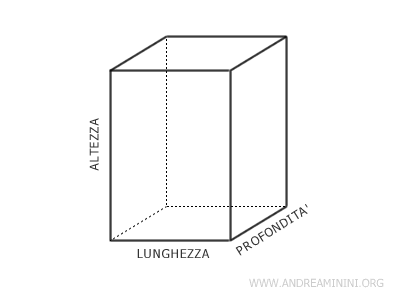
Nella geometria solida la lunghezza è una delle tre dimensioni, insieme all'altezza e alla profondità (o larghezza), necessarie per misurare la dimensione di un oggetto.
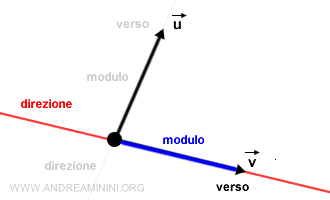
In algebra lineare la lunghezza (o magnitudine) è il modulo di un vettore, è sinonimo di norma o di valore assoluto, ecc.
Un vettore è generalmente indicato con una freccia e il modulo del vettore è la lunghezza della freccia.
Quindi, per comprendere il significato del termine "lunghezza" bisogna fare attenzione al contesto in cui viene utilizzato.
La lunghezza come grandezza fisica
In fisica la lunghezza è la grandezza fisica fondamentale, si misura con il metro (m) ed è indicata con [L] nelle analisi dimensionali.
L'unità di misura della lunghezza è il metro (m) che oggi viene definito come lo spazio percorso dalla luce in una frazione di secondo.
$$ 1 \ \text{metro} = c \cdot \frac{1 \ s}{299.792.458} $$
Dove \( c = 299.792.458 \ \text{m/s} \) è la velocità della luce nel vuoto.
Nota. Poiché la velocità della luce $ c $ è un rapporto tra la lunghezza e il tempo, anche l'analisi dimensionale conferma la relazione. $$ \left[ L \right] = \left[\frac{L}{T}\right] \cdot \left[T\right] = \left[L\right] $$
La storia dell'unità di misura della lunghezza
In passato, molte unità di lunghezza erano legate al corpo umano, poiché erano facilmente accessibili.
Ad esempio, il cubito nell'antico Egitto era pari alla distanza tra il gomito e la punta del dito medio. Il piede, invece, era basato sulla lunghezza del piede umano ed è stato adottato in varie culture.
Tuttavia, queste unità erano imprecise e variabili, poiché le dimensioni del corpo umano differiscono da persona a persona, rendendo difficile standardizzare le misurazioni.
Nel 1793, durante la rivoluzione francese, l'Accademia francese delle scienze introdusse il metro come tentativo di creare un'unità di misura standard e universale.
Il metro venne definito come la quarantamilionesima parte della lunghezza del meridiano terrestre che collega il Polo Nord con l'Equatore, passando per Parigi. Questa definizione legava la lunghezza a un fenomeno naturale e misurabile.
Nel 1889, per facilitare la standardizzazione, venne creato un campione fisico del metro, rappresentato da una barra di platino-iridio conservata a Parigi.
Questa barra, con due tacche che distavano esattamente un metro, divenne il riferimento internazionale. Copie della barra furono distribuite in tutto il mondo per assicurare uniformità nelle misurazioni.
Nel 1960, con i progressi della fisica, si abbandonò il campione fisico a favore di una definizione basata su fenomeni naturali. Il metro venne ridefinito in termini di una specifica lunghezza d'onda della radiazione emessa dall'atomo di kripton-86, consentendo una misurazione molto più precisa e replicabile.
Nel 1983, il metro venne ulteriormente raffinato con una definizione basata sulla velocità della luce. Si stabilì che il metro fosse la distanza percorsa dalla luce nel vuoto in 1/299.792.458 di secondo. Questa definizione sfrutta il fatto che la velocità della luce è una costante fondamentale e immutabile, garantendo una precisione assoluta.
Il metro ha percorso un lungo cammino, passando da misure arbitrarie basate sul corpo umano a una definizione fondata su costanti fisiche fondamentali.
Questa evoluzione ha permesso di ottenere misurazioni sempre più precise e uniformi, essenziali per il progresso scientifico e tecnologico.
Nota. L'unità di misura delle distanze varia a seconda della scala. Ad esempio, per misurare le distanze su scala astronomica non si usa il metro ma altre unità di misura come l'Unità Astronomica (UA), l'anno luce (a.l.) e il parsec. L'Unità Astronomica (UA) è l'unità di misura delle distanze che si usa per descrivere le distanze all'interno del Sistema Solare. E' definita come la distanza media tra la Terra e il Sole e 1 UA corrisponde a circa 149.597.870,7 chilometri (circa 150 milioni di chilometri). Ad esempio, Giove si trova a circa 5,2 UA dal Sole. L'anno luce (a.l.) è un'unità di misura utilizzata per descrivere le distanze interstellari, cioè tra le stelle o tra sistemi stellari. Un anno luce corrisponde alla distanza che la luce percorre nel vuoto in un anno, ossia circa 9,46 trilioni di chilometri (9,46 x 1012 km) ovvero quasi diecimila miliardi di chilometri. Un'altra unità utilizzata spesso in astronomia è il parsec, che corrisponde a circa 3,26 anni luce o 3,086 x 1013 chilometri.
La lunghezza da grandezza assoluta a grandezza relativa
Nella fisica classica del XIX secolo la lunghezza era considerata come una grandezza assoluta, indipendente dal tempo.
Questa certezza crollò nel XX secolo con la teoria della relatività ristretta di Einstein
La lunghezza assume una nuova dimensione, perde il significato di misura assoluta per assumere un'accezione di misura relativa.
Ad esempio, la lunghezza di un oggetto in movimento è più corta rispetto a quella misurata da un osservatore in stato di quiete, un fenomeno noto come contrazione delle lunghezze.
Questo effetto si verifica a velocità prossime a quella della luce.
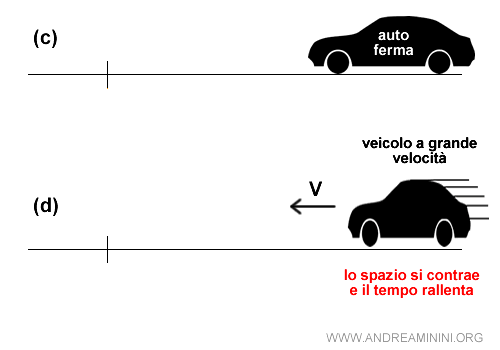
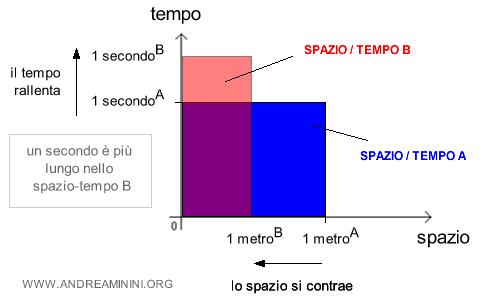
Inoltre, nella teoria generale di Einstein lo spazio e il tempo sono viste come grandezze interdipendenti e non più come entità fisiche separate.
Lo spaziotempo diventa un tessuto unificato che definisce la struttura dell'universo.
In questo contesto, gli eventi non sono più localizzati in punti isolati di spazio e istanti discreti di tempo, ma piuttosto in coordinate spaziotemporali che evidenziano l'interazione inscindibile tra lo spazio e il tempo.
La misurazione della lunghezza
Nella misurazione della lunghezza, precisione e accuratezza sono fondamentali.
La precisione si riferisce alla capacità di uno strumento di fornire risultati ripetibili e coerenti, mentre l'accuratezza indica quanto una misurazione si avvicina al valore reale.
Gli strumenti per misurare una lunghezza variano dalla semplice riga graduata, al calibro a corsoio, agli strumenti più sofisticati come il micrometro, i laser e i dispositivi GPS.
In laboratorio, le lunghezze possono essere misurate con estrema precisione utilizzando interferometri.
Strumenti che utilizzano la luce laser per misurare distanze. Funzionano calcolando il tempo che la luce impiega a riflettersi su un oggetto e tornare allo strumento.
La scelta dello strumento di misurazione della lunghezza dipende dal grado di precisione e accuratezza richiesti.
Nota. Mentre strumenti semplici come righe e calibri sono adeguati per misurazioni quotidiane o industriali, tecnologie più avanzate come laser, GPS e interferometri sono indispensabili per misurazioni complesse e di estrema precisione in laboratori e applicazioni scientifiche.
Le operazioni tra le lunghezza
In geometria euclidea le proprietà delle operazioni matematiche sono valide anche nelle operazioni tra le lunghezze.
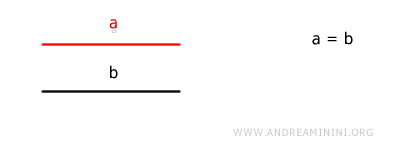
La lunghezza di un segmento è normalmente indicata con una lettera minuscola (es. a, b, c, ...).
Ad esempio, la congruenza dei segmenti equivale all'uguaglianza tra due lunghezze (a=b).
$$ a = b $$
Confrontando due segmenti non congruenti si può capire se uno dei due è maggiore o minore dell'altro (a<b oppure a>b).
$$ a < b $$
La somma di due segmenti è uguale alla lunghezza di un segmento ottenuto concatenando gli estremi dei segmenti tra loro.
$$ a + b = c $$
La somma di due segmenti soddisfa le seguenti proprietà:
- Commutativa $$ a+b = b+a $$
- Associativa $$ (a+b)+c = a+(b+c) $$
- Esistenza dell'elemento neutro $$ a+0 = 0+a = a $$
E così via.
