Piani paralleli, coincidenti e incidenti nello spazio
Due piani nello spazio R3 possono essere paralleli, coincidenti o incidenti.
- Sono piani paralleli se non hanno punti in comune.
- Sono piani coincidenti se sono paralleli e hanno in comune tutti i punti del piano.
- Sono piani incidenti se hanno in comune gli infiniti punti della retta incidente tra i due piani.
In altre parole, quando i piani sono incidenti, l'intersezione è sempre una retta, mentre nel caso parallelo o coincidente, l'intersezione è assente o coincide con l'intero piano stesso.
Nota. I piani paralleli e coincidenti condividono la stessa direzione delle normali, ma differiscono per la posizione relativa. I piani incidenti, invece, intersecano formando una retta comune, ma le loro normali non sono parallele.
Come verificare se due piani sono paralleli, coincidenti o incidenti
Per capire se due piani sono paralleli, coincidenti o incidenti nello spazio, devo analizzare la dipendenza lineare dei vettori direttori dei piani.
- Se i vettori sono linearmente dipendenti, i piani sono paralleli o coincidenti.
- Se i vettori sono linearmente indipendenti, i piani sono incidenti.
Come si misura la dipendenza lineare dei vettori?
I due piani sono identificati da due equazioni vettoriali/parametriche.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$
$$ \begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} = \begin{pmatrix} x'_0 \\ y'_0 \\ z'_0 \end{pmatrix} + t_1 \begin{pmatrix} l_3 \\ m_3 \\ n_3 \end{pmatrix} + t_2 \begin{pmatrix} l_4 \\ m_4 \\ n_4 \end{pmatrix} $$
Prendo i quattro vettori direttori e li dispongo in colonna in una matrice.
$$ \begin{pmatrix} l_1 & l_2 &l_3 &l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix}$$
Poi calcolo il rango della matrice.
- Se il rango della matrice è uguale o inferiore a 2, i vettori sono linearmente dipendenti. I due piani sono paralleli oppure coincidenti. $$ r_k \begin{pmatrix} l_1 & l_2 &l_3 &l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} \le 2 $$
Nota. Per capire se sono paralleli o coincidenti, basta verificare se un punto di un piano appartiene anche all'altro. Se il punto appartiene a entrambi i piani, i piani sono coincidenti. Viceversa, sono paralleli.
- Se il rango della matrice è uguale a 3, i vettori sono linearmente indipendenti. I due piani sono incidenti. $$ r_k \begin{pmatrix} l_1 & l_2 &l_3 &l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} = 3 $$
Quindi, se le equazioni dei piani sono in forma parametrica la regola da seguire è la seguente:
| Rango della matrice | Relazione tra i vettori | Posizione reciproca dei piani |
|---|---|---|
| 1-2 | Linearmente dipendenti | Piani coincidenti o paralleli distinti |
| 3 | Linearmente indipendenti | Piani incidenti (si intersecano lungo una retta) |
Il caso delle equazioni cartesiane
Nel caso delle equazioni cartesiane del piano
$$ a_1 x + b_1 y+ c_1 z + d_1 = 0$$
$$ a_2 x + b_2 y+ c_2 z + d_2 = 0$$
i vettori sono linearmente dipendenti se il rango della matrice dei coefficienti è uguale a 1.
In questo caso i piani sono paralleli o coincidenti.
$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{pmatrix} = 1 $$
Viceversa, i vettori sono linearmente indipendenti se il rango della matrice dei coefficienti è uguale a 2.
In questo caso i piani sono incidenti.
$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{pmatrix} = 2 $$
Quindi, se le equazioni dei piani sono in forma cartesiana la regola da seguire è la seguente:
| Rango della matrice | Relazione tra i vettori | Posizione reciproca dei piani |
|---|---|---|
| 1 | Linearmente dipendenti | Piani coincidenti o paralleli distinti |
| 2 | Linearmente indipendenti | Piani incidenti (si intersecano lungo una retta) |
Esempio
Esempio 1 ( equazioni parametriche )
Ho due piani nello spazio
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix} + t_2 \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
Metto i vettori direttori in matrice.
Poi calcolo il rango.
$$ r_k \begin{pmatrix} 0 & 2 & 0 & 1 \\ -1 & -1 & -3 & -1 \\ 2 & 0 & 6 & 1 \end{pmatrix} = 2$$
Il rango della matrice è due.
Quindi, i vettori sono linearmente dipendenti.
Il piano è parallelo distinto o coincidente.
Come verifico se i piani sono paralleli o coincidenti?
Prendo un punto della prima retta e verifico se appartiene anche all'altra.
So già che P(0,0,0) appartiene al primo piano.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix} + t_2 \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} $$
Sostituisco le coordinate (0,0,0) nell'equazione del secondo piano e verifico se l'equazione è soddisfatta.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
$$ \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
La trasformo in equazione parametrica.
$$ \begin{cases} 0 = 0 + t_2 \\ 0 = 1 -3t_1 -t_2 \\ 0 = 0 +6t_1 +t_2 \end{cases} $$
$$ \begin{cases} t_2 = 0 \\ 1 -3t_1 - (0) = 0 \\ 6t_1 + (0) = 0 \end{cases} $$
$$ \begin{cases} t_2 = 0 \\ t_1 = \frac{1}{3} \\ 6t_1 = 0 \end{cases} $$
Il sistema non ha una soluzione.
Il punto P(0,0,0) non appartiene al secondo piano e i due piani non sono coincidenti.
Quindi, sono due piani paralleli.
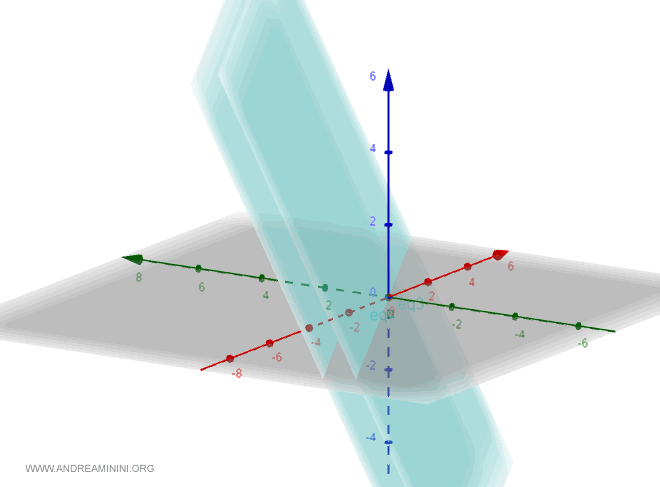
Esempio equazioni cartesiane
Ho due equazioni cartesiane:
$$ x+2y+z=0 $$
$$ 2x+4y+2z-5=0 $$
Costruisco la matrice dei coefficienti.
$$ \begin{pmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \end{pmatrix} $$
Poi calcolo il rango della matrice
$$ r_k \begin{pmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \end{pmatrix} = 1 $$
Il rango della matrice è uguale a 1.
Quindi i vettori sono linearmente dipendenti, ossia paralleli o incidenti.
Come verificare se sono piani paralleli o incidenti?
Calcolo le coordinate di un punto della prima equazione mettendo a zero due coordinate a mia scelta.
Ad esempio, x=0 e y=0.
$$ x+2y+z=0 $$
$$ 0+20+z=0 $$
$$ z=0 $$
Ottengo così le coordinate di un punto del primo piano.
$$ P ( x,y,z ) = P(0,0,0 ) $$
Sostituisco le coordinate del punto P(0,0,0) nell'equazione del secondo piano.
$$ 2x+4y+2z-5=0 $$
$$ 2(0)+4(0)+2(0)-5=0 $$
$$ -5=0 $$
L'equazione non è soddisfatta.
Pertanto il punto del primo piano P(0,0,0) non appartiene anche al secondo piano.
I due piani non possono essere coincidenti.
So due piani paralleli.

Note
Alcune note aggiuntive sui piani paralleli o inclinati.
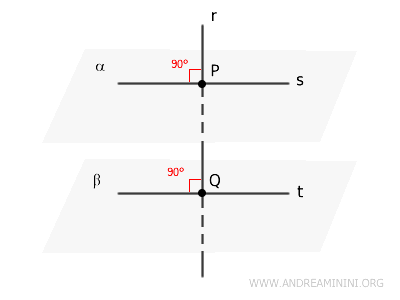
- Teorema della retta perpendicolare a due piani
Se due piani \( \alpha \) e \( \beta \) sono perpendicolari a una retta \( r \) in due punti distinti \( P \) e \( Q \) della retta, allora i due piani sono paralleli.
- Teorema dei piani paralleli intersecati da un terzo piano
Se un piano \( \pi \) interseca due piani paralleli \( \pi_1 \) e \( \pi_2 \), le intersezioni sono due rette parallele.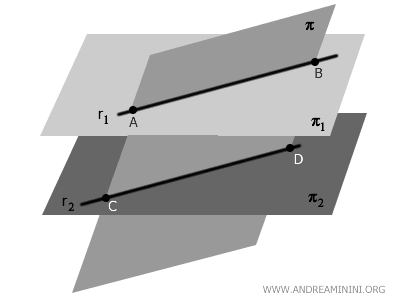
Questo si verifica perché, essendo \( \pi_1 \) e \( \pi_2 \) equidistanti e paralleli, il piano \( \pi \) li interseca formando due rette \( r_1 \) e \( r_2 \). Poiché \( \pi \) mantiene lo stesso angolo di intersezione con entrambi i piani, le rette \( r_1 \) e \( r_2 \) risultano parallele.
E così via.
