Le grandezze geometriche

Le classi di grandezze geometriche sono un concetto fondamentale in matematica e geometria.

Queste classi includono varie misure e proprietà di figure e forme, come lunghezza, area, volume, angoli, e altre.

Alcuni esempi di classi di grandezze geometriche

Tra le grandezze geometriche più comuni ci sono le seguenti:

• Lunghezza
  Si riferisce alla misura di una linea retta da un punto all'altro. È la dimensione più semplice e viene misurata tramite diverse unità di misura come metri, centimetri, pollici, ecc.
• Area
  L'area è la misura dello spazio bidimensionale (piano) all'interno di una figura. Per esempio, l'area di un quadrato o di un cerchio. Viene misurata in unità quadrate come metri quadrati, centimetri quadrati, ecc.
• Volume
  Il volume misura lo spazio tridimensionale occupato da un oggetto. Ad esempio, il volume di una sfera o di un cubo. Viene misurato in unità cubiche come metri cubi, centimetri cubi, ecc.
• Angoli
  Gli angoli orientabili sono misure che indicano la deviazione tra due linee che si incontrano in un punto in comune detto "vertice". Sono misurati in gradi o radianti.
• Superficie
  E' una classe generale che include anche l'area delle figure piane (bidimensionali) e l'area totale che copre l'esterno di un oggetto tridimensionale.

Queste grandezze sono essenziali per studiare e comprendere le proprietà delle forme geometriche sia in matematica pura che nelle sue applicazioni pratiche.

Le grandezze geometriche omogenee

Le grandezze sono considerate grandezze omogenee quando appartengono alla stessa classe geometrica.

In altre parole, due grandezze sono omogenee se possono essere direttamente confrontate o combinate tra loro perché hanno la stessa natura o dimensione.

Ad esempio, due o più lunghezze sono omogenee se sono misurate nella stessa unità (come metri, chilometri, pollici, ecc.) e quindi possono essere sommate o sottratte.

5 metri e 3 metri sono grandezze omogenee.

Allo stesso modo sono omogenee le aree se sono misurate nella stessa unità (come metri quadrati, ettari, acri, ecc.).

Due volumi sono omogenei se espressi nella stessa unità di misura (come litri, metri cubi, ecc.).

Gli angoli sono omogenei quando sono misurati nella stessa unità, come gradi o radianti.

Non posso combinare direttamente grandezze non omogenee. Ad esempio, non ha senso sommare una lunghezza e un'area, o un volume e un angolo, perché appartengono a classi di grandezza diverse. Tuttavia, spesso è possibile convertire le grandezze in unità compatibili, se necessario, per renderle omogenee.

I multipli e i sottomultipli di una grandezza

Una grandezza A si dice multiplo di una grandezza omogenea B, se è n volte la grandezza B. $$ A = n \cdot B $$ Dove n è un numero naturale maggiore o uguale a zero (n≥0).

Quando si parla del multiplo di una grandezza A secondo un numero naturale n, si considera una grandezza B, che è omogenea ad A. Questo significa che B e A sono dello stesso tipo o natura (per esempio, entrambe possono essere lunghezze, tempi, masse, ecc.).

Ecco come definire A in termini di B e n:

• Se n è maggiore o uguale a 1
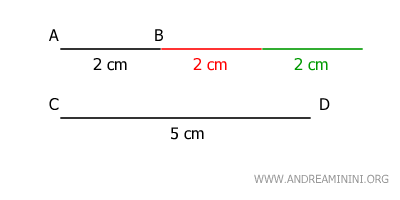
  In questo caso, A è la somma di n grandezze uguali ad B.

  Ad esempio, considero due segmenti AB e CD. Sono due grandezze omogenee perché sono entrambe due lunghezze. Se il segmento CD è tre volte (n=3) il segmento AB e il segmento AB è una lunghezza di 2 metri, allora il segmento CD è una lunghezza di 6 metri ed è una grandezza multipla del segmento AB per un numero naturale n=3. $$ \overline{CD} = 3 \cdot \overline{AB} $$
  /geometria/grandezze-commensurabili-e-incommensurabili

• Se n è uguale a 1
  In questo caso A è semplicemente uguale ad B. Questo è ovvio, poiché la somma di una grandezza con se stessa una sola volta è la grandezza stessa. $$ A=B $$
• Se n è uguale a 0
  In questo caso A è la grandezza nulla ossia zero. In termini pratici, se non moltiplico una grandezza per alcun fattore (zero volte), ottengo una grandezza nulla. $$ A= 0 \cdot B = 0 $$

Per ottenere la definizione di sottomultiplo mi basta invertire la relazione di multiplo.

Se la grandezza A è un multiplo di B, allora B è un sottomultiplo di A. $$ B = \frac{1}{n} \cdot A $$ Dove n è sempre un numero naturale maggiore di zero (n>0).

In altre parole, la grandezza B è una frazione o una parte di A.

In questo caso evito di considerare il caso n=0 perché si verificherebbe una divisione per zero, ovvero un'operazione matematica impossibile.

Ad esempio, se il segmento CD è un multiplo di AB per un numero naturale n=3, allora il segmento AB è un sottomultiplo di CD per una frazione di 1/3. $$ \overline{AB} = \frac{1}{3} \cdot \overline{CD} $$
/geometria/grandezze-commensurabili-e-incommensurabili

Osservazioni

Alcune osservazioni e note a margine sulle classi delle grandezze geometriche

• Le classi geometriche sono gruppi?
  Le classi geometriche non sono gruppi nel senso algebrico perché non sono definite da un'operazione che soddisfa le proprietà dei gruppi.

  Le classi geometriche organizzano e categorizzano forme e figure sulla base di proprietà condivise, i gruppi invece sono strutture algebriche che definiscono un modo preciso per combinare gli elementi di un insieme.

• Il postulato di Eudosso-Archimede
  Il postulato stabilisce che se si ha una grandezza minore di un'altra, è sempre possibile aggiungere un numero sufficiente di copie di questa prima grandezza per superare la seconda.
  
  

  Nota. Ovviamente le grandezze devono essere entrambe non nulle. Se la grandezza minore fosse nulla, tutti i suoi multipli sarebbero nulli. Quindi, non esisterebbe alcun multiplo in grado di superare la grandezza maggiore.

• Le grandezze geometriche commensurabili e incommensurabili
  Due grandezze geometriche omogenee sono commensurabili se esiste un numero razionale m/n che le mette in relazione. Viceversa, se non esiste, le grandezze sono incommensurabili.

  Esempio. Le lunghezze dei segmenti AB e CD sono grandezze commensurabili
  
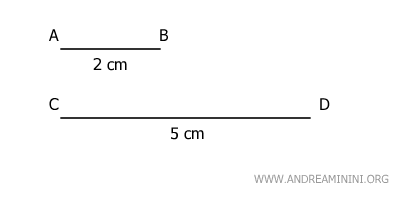
  perché esiste un numero razionale m/n che le mette in relazione tra loro. $$ \overline{AB} = \frac{2}{5} \cdot \overline{CD} $$ Dove m e n sono due numeri interi.

E così via.