Superfici equivalenti

Due superfici A e B sono superfici equivalenti quando hanno la stessa estensione. $$ A \doteq B $$

Nella geometria euclidea del piano questo vuol dire che le superfici sono equivalenti se hanno la stessa area.

$$ Area(A) = Area(B) $$

Questo è il caso più comune e intuitivo di equivalenza.

Ad esempio, un quadrato e un triangolo sono superfici equivalenti se le loro aree sono uguali, anche se le loro forme sono diverse.

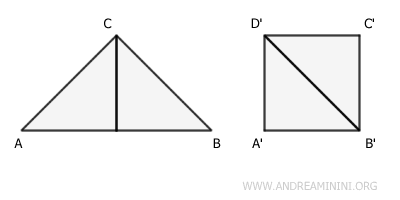
Tutte le superifici che hanno la stessa estensione (area) appartengono alla stessa classe di equivalenza.

Le proprietà delle superfici equivalenti

L'equivalenza tra superfici è una relazione di equivalenza, quindi soddisfa le seguenti proprietà:

• Proprietà riflessiva
  Una superficie è sempre equivalente a se stessa. $$ A \doteq A $$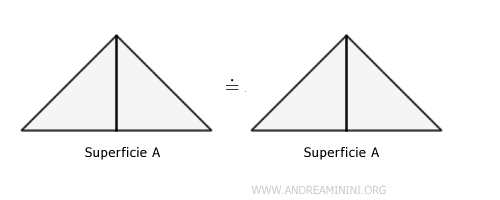

  

• Proprietà simmetrica
  Se una superficie A è equivalente alla superficie B, allora anche la superficie B è equivalente alla superficie A. $$ A \doteq B \Leftrightarrow B \doteq A $$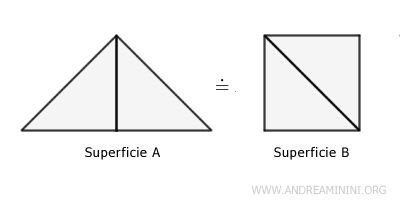

  

• Proprietà transitiva
  Se una superficie A è equivalente alla superficie B e quest'ultima è equivalente alla superficie C, allora la superficie A è equivalente anche alla superficie C. $$ A \doteq B \ , \ B \doteq C \Longrightarrow A \doteq C $$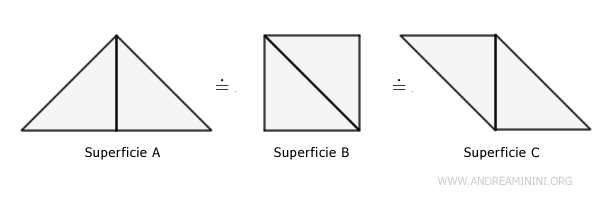

  

Sono concetti chiave nella matematica, che vanno oltre la semplice geometria, perché sono soddisfatti da tutte le relazioni di equivalenza.

Osservazioni

Alcune osservazioni e note aggiuntive sulle superfici equivalenti.

• Postulato di De Zolt
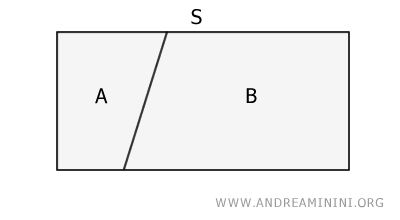
  Una superficie non è equivalente a una sua parte.

  Esempio. La superficie S è suddivisa in due parti A e B. L'area della superficie S è la somma delle aree delle superfici A e B. Quindi, S non può essere equivalente alla superficie A, né a B.
  

• Due superfici congruenti sono sempre equivalenti, ma non è detto il contrario
  Ad esempio, due triangoli congruenti hanno la stessa lunghezza dei lati e ampiezza degli angoli nello stesso ordine. Quindi, hanno la stessa area e sono superfici equivalenti.
  
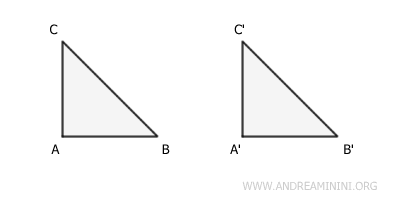
  Viceversa, un triangolo ABC e un quadrato ABCD con la stessa area sono superfici equivalenti ma non sono congruenti perché non sono sovrapponibili punto a punto con un movimento rigido. Hanno lati e angoli differenti.
  
• Se considero due coppie di superfici equivalenti $$ S_1 \doteq S_2 $$ $$ S_3 \doteq S_4 $$ e le sommo membro a membro tra loro, la somma delle superfici è a sua volta equivalente $$ S_1 + S_3 \doteq S_2 + S_4 $$

  Esempio
  

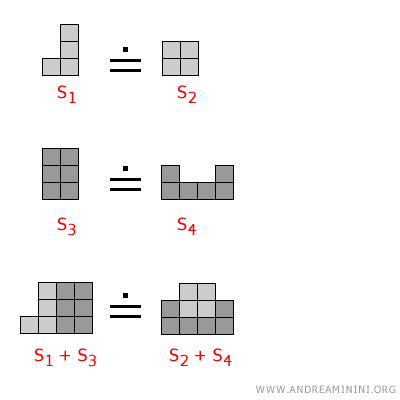
• Principio di equiscomponibilità
  Due figure equiscomponibili, cioè scomponibili nello stesso numero di parti congruenti, sono equivalenti.
  
• Date due figure congruenti, se sottraggo o aggiungo delle parti congruenti, ottengo delle figure equivalenti.
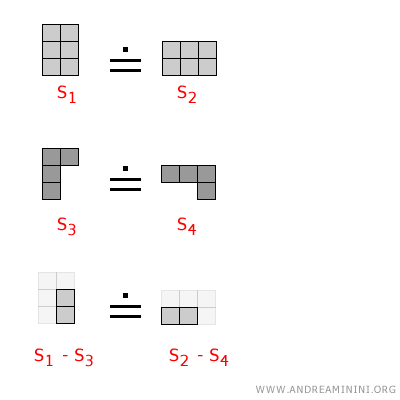
• Se considero due coppie di superfici equivalenti $$ S_1 \doteq S_2 $$ $$ S_3 \doteq S_4 $$ e le sottraggo membro a membro, la differenza delle superfici è a sua volta equivalente $$ S_1 - S_3 \doteq S_2 - S_4 $$

  Esempio
  

E così via.