La congruenza in geometria

Due figure geometriche sono dette congruenti se sono sovrapponibili punto a punto tramite un movimento rigido.

Dove il movimento rigido è lo spostamento della figura senza deformazione tramite una traslazione, una rotazione e/o una riflessione.

Pertanto, due figure congruenti hanno la stessa forma e dimensione ma occupano una diversa posizione nello spazio.

Per indicare una congruenza si utilizza il simbolo "circa uguale" ossia un uguale con una tilde sopra ≅

$$ A ≅ B $$

Il concetto di congruenza è fondamentale per l'identificazione e la comparazione delle figure geometriche.

Nota. Il concetto di congruenza viene introdotto nel contesto della geometria euclidea. Si basa su trasformazioni rigide, o isometrie, come traslazioni, rotazioni e riflessioni. Queste trasformazioni alterano la posizione di una figura nello spazio, ma non la sua forma o dimensione. Pertanto, se una figura può essere mappata su un'altra tramite una serie di isometrie, le due figure sono congruenti.

Un esempio pratico

Considero due copie dello stesso triangolo,

Una copia è capovolta rispetto all'altra.

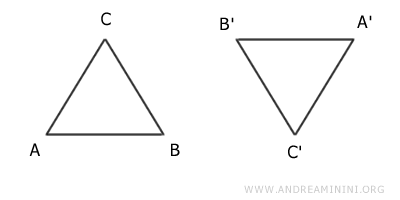
Questi due triangoli non sono uguali perché, pur avendo la stessa forma e dimensione, non occupano lo stesso spazio.

I due triangoli sono congruenti perché hanno la stessa forma e dimensioni e posso sovrapporli dopo una rotazione e una traslazione.

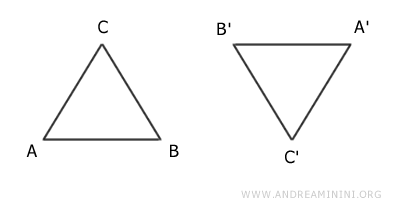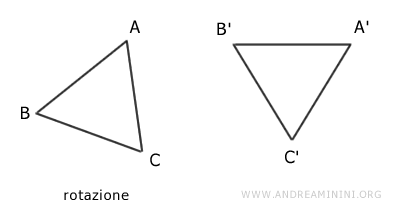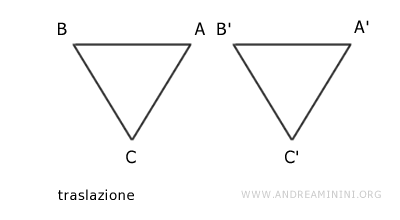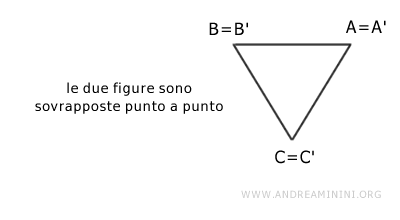
Una volta sovrapposti, allora le due figure geometriche diventano uguali.

Altri esempi di congruenze

In particolare, nella geometria del piano:

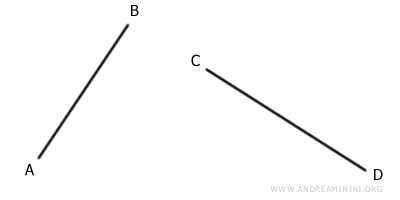
1. Due segmenti sono congruenti se hanno la stessa lunghezza. Ad esempio, AB≅CD
   
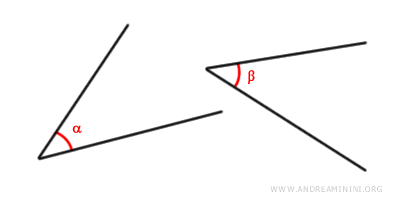
2. Due angoli sono congruenti se hanno la stessa ampiezza. Ad esempio, α≅β
   
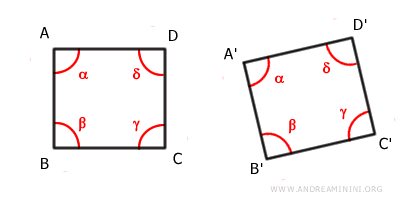
3. Due poligoni sono congruenti se i loro lati corrispondenti sono congruenti e i loro angoli corrispondenti sono congruenti.
   

In altre parole, per stabilire la congruenza tra due figure geometriche, devono essere rispettati determinati criteri.

Ad esempio, due triangoli sono congruenti se rispettano uno dei seguenti criteri di congruenza

• Criterio dei tre lati o LLL
  due triangoli sono congruenti se hanno i tre lati congruenti, ossia della stessa lunghezza.
• Criterio del lato-angolo-lato o LAL
  due triangoli sono congruenti se hanno due lati e l'angolo compreso congruenti.
• Criterio dell'angolo-lato-angolo o ALA
  due triangoli sono congruenti se hanno due angoli e il lato compreso congruenti.

Nota. Questi criteri di congruenza sono specifici per i triangoli. Se due triangoli soddisfano uno dei precedenti criteri di congruenza, allora soddisfano anche gli altri. Pertanto, è sufficiente verificare un solo criterio per stabilire la congruenza dei triangoli.

Qual è la differenza tra congruenza e uguaglianza?

I termini "congruenza" e "uguaglianza" sono spesso usati in modo intercambiabile, ma in geometria e matematica hanno significati diversi.

Due figure sono uguali se coincidono punto a punto, senza fare alcun movimento rigido.

Pertanto, due figure geometriche uguali occupano esattamente lo stesso spazio, hanno la stessa forma, le stesse dimensioni e la stessa posizione.

Per indicare un'uguaglianza in geometria si utilizza il simbolo uguale della matematica ossia "="

$$ A = B $$

Ad esempio, l'altezza e la mediana di un triangolo isoscele sono uguali perché coincidono punto a punto.

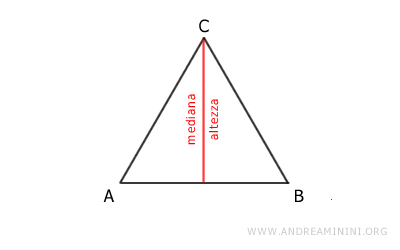
La congruenza, invece, richiede che due figure siano sovrapponibili punto a punto dopo un movimento rigido.

Pertanto, due figure congruenti hanno la stessa forma e dimensione ma una diversa posizione, ossia occupano uno spazio diverso.

Per indicare una congruenza in geometria si usa il simbolo "circa uguale", è un uguale con una tilde sopra ≅

$$ A ≅ B $$

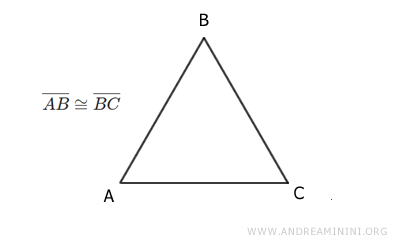
Ad esempio, i cateti AB e BC del triangolo isoscele sono congruenti perché posso sovrapporli dopo una rotazione e una traslazione.

In conclusione, la congruenza è una versione più flessibile dell'uguaglianza, specifica per la geometria, che consente a figure di forma e dimensione identica di avere posizioni diverse.

La differenza tra congruenza e similitudine

La congruenza si distingue anche dalla similitudine.

Nella similitudine le figure geometriche hanno la stessa forma ma dimensioni diverse.

Ad esempio, questi due triangoli non sono congruenti perché non sono sovrapponibili.

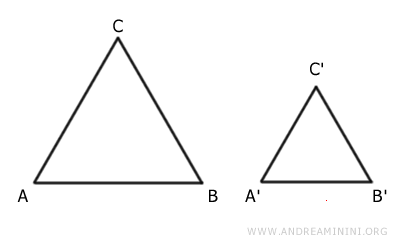
I due triangoli sono però simili perché hanno entrambi la stessa forma, sono triangoli isoscele, ma una dimensione diversa.

Il primo triangolo isoscele ha i lati più lunghi rispetto al secondo.

Le proprietà della congruenza

È importante notare che la congruenza è una relazione di equivalenza, il che significa che soddisfa le proprietà di riflessività, simmetria e transitività

1. Riflessività
   ogni figura è congruente a se stessa
2. Simmetria
   se la figura A è congruente alla figura B, allora la figura B è congruente alla figura A
3. Transitività
   se la figura A è congruente alla figura B e la figura B è congruente alla figura C, allora la figura A è congruente alla figura C.

E così via.