La trasformazione geometrica
Una trasformazione geometrica è una corrispondenza biunivoca tra ogni punto del piano (o dello spazio) e un altro punto dello stesso piano (o spazio).
Esistono diverse trasformazioni geometriche: rotazioni, traslazioni, isometrie, ecc.
In termini formali, una trasformazione geometrica è una qualsiasi applicazione T invertibile che associa ogni punto P di un insieme non vuoto X a un punto P' dell'insieme Y.
$$ T: X \rightarrow Y $$
Dove l'insieme Y è l'immagine T(X) dell'insieme X rispetto all'applicazione T.
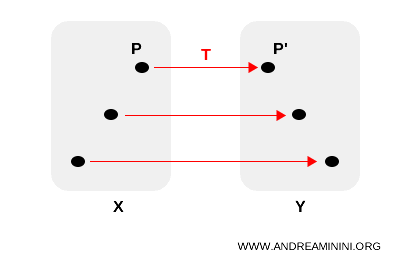
Il punto P' di Y è detto immagine o trasformato di P, mentre il punto P di X è detto controimmagine o antitrasformato.
In parole più semplici, le trasformazioni geometriche sono operazioni matematiche che modificano la posizione o la forma di un oggetto in uno spazio geometrico. Le trasformazioni possono essere applicate a varie entità geometriche, come punti, linee, forme e figure solide.
Poiché la trasformazione è biunivoca, esiste anche una trasformazione inversa $ T^{-1}: Y \rightarrow X $ che associa ogni punto dell'insieme Y a un punto dell'insieme X.
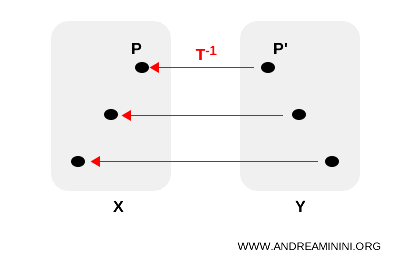
Le proprietà geometriche che si conservano dopo una trasformazione sono dette invarianti.
Un esempio
Considero una figura geometrica ABC.
Se ruoto una figura geometrica per un determinato angolo alfa, ottengo una corrispondenza biunivoca tra i punti A e A', B e B', C e C'.
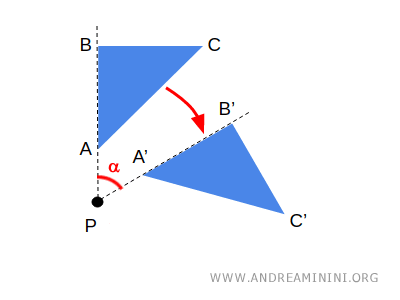
I punti A', B' e C' dopo la trasformazione sono rispettivamente detti immagini o trasformati dei punti A, B, C.
Considerando la rotazione come una funzione biettiva f, posso anche scrivere
$$ A' = f(A) $$
$$ B' = f(B) $$
$$ C' = f(C) $$
Questa notazione si legge "A' è uguale a effe di A", e via dicendo.
E ovviamente lo stesso vale anche tra tutti gli altri punti e segmenti della figura.
Ad esempio, il segmento A'B' è l'immagine del segmento AB.
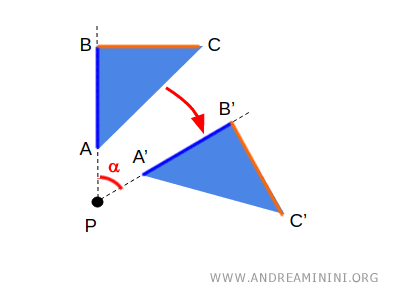
Questo è un esempio pratico di trasformazione geometrica.
Nota. In questo esempio, il punto P ha un'immagine che corrisponde a se stesso. In altre parole, il punto P non cambia la sua posizione nel piano dopo la rotazione. In questo caso si dice che P è un punto unito.
Tipi trasformazioni geometriche
Esistono diversi tipi di trasformazioni geometriche.
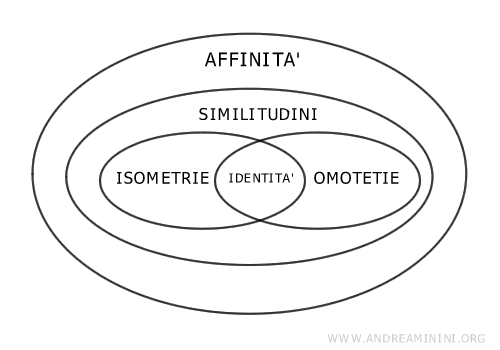
Ecco un elenco delle principali trasformazioni geometriche:
- Traslazione
Spostamento di tutti i punti di una figura di una distanza costante in una direzione specificata. La figura traslata mantiene la stessa forma e dimensione dell'originale.
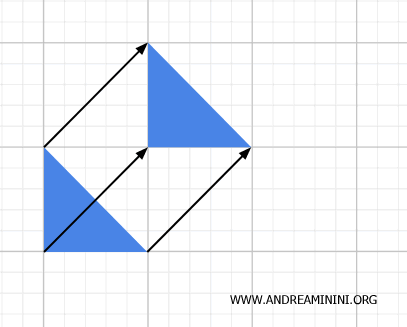
- Rotazione
Movimento circolare di una figura intorno a un punto fisso (centro di rotazione). La distanza di ogni punto della figura dal centro di rotazione rimane costante.

- Riflessione (o specchiamento)
Ribaltamento di una figura rispetto a una linea (asse di riflessione), creando un'immagine speculare.
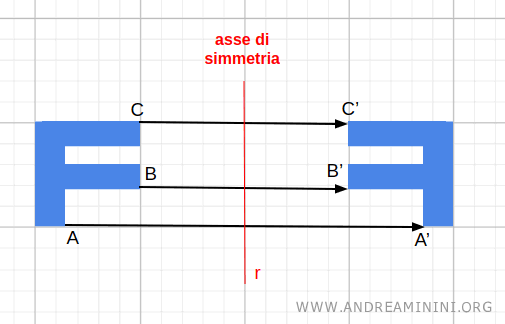
- Isometria
Le isometrie sono trasformazioni geometriche che preservano le distanze tra i punti e le dimensioni degli oggetti. Ad esempio, la traslazione, la rotazione e la riflessione sono trasformazioni isometriche. - Omotezia (o scalatura)
Non preserva le dimensioni ma mantiene le proporzioni e le forme generali degli oggetti. Cambia la dimensione di una figura attraverso la moltiplicazione delle distanze di tutti i suoi punti da un punto fisso (centro di omotezia) per un fattore costante.
Le trasformazioni geometriche nella geometria analitica
Una trasformazione geometrica è rappresentata da un sistema di equazioni lineari che ammette una e una sola soluzione per ogni coppia di coordinate. $$ \begin{cases} x' = ax + by + c \\ y' = dx + ey + f \end{cases} $$ Dove $x, y$ sono le coordinate del punto iniziale, $x', y'$ sono le coordinate del punto trasformato, mentre $a, b, c, d, e, f$ sono i coefficienti della trasformazione.
In altre parole, a ogni punto $(x, y)$ corrisponde uno e un solo* $(x', y')$ e viceversa da ogni $(x', y')$ si può ricavare un solo $(x, y)$
Questo succede solo se il sistema lineare ha una soluzione unica. cioè se il determinante è diverso da zero.
$$
\Delta =
\begin{vmatrix}
a & b \\
d & e
\end{vmatrix}
= ae - bd \neq 0
$$
Perché deve essere un sistema lineare? Le funzioni lineari garantiscono che la trasformazione sia continua (nessun salto) e biunivoca (cioè invertibile). Il determinante della matrice dei coefficienti diverso da zero garantisce che ci sia un'unica soluzione per ogni punto del piano o dello spazio.
Esempio
Considero il sistema di equazioni lineari
$$
\begin{cases}
x' = 2x - 3y + 5 \\
y' = x + 4y - 2
\end{cases}
$$
Si tratta di un sistema affine perché nella parte con $ x $ e $ y $ aggiunge dei termini noti (5 e -2).
Lo riscrivo in questa forma più semplice:
$$
\begin{cases}
2x - 3y = x' - 5 \\
x + 4y = y' + 2
\end{cases}
$$
La matrice dei coefficienti è
$$\begin{pmatrix} 2 & -3 \\ 1 & 4 \end{pmatrix}$$
A questo punto, calcolo il determinante della matrice dei coefficienti per verificare che sa diverso da zero ossia che il sistema abbia un'unica soluzione.
$$ \Delta= \begin{vmatrix} 2 & -3 \\ 1 & 4 \end{vmatrix} = 2⋅4−(−3)⋅1=8+3=11 \ne 0 $$
Il determinante è non nullo, quindi la trasformazione è invertibile e biunivoca, ovvero è una trasformazione geometrica.
Questo significa che ogni punto ha un’unica immagine e un’unica pre-immagine.
Esempio. Considero un punto $A(1, 2)$ la cui trasformazione geometrica è la seguente: $$
\begin{cases}
x' = 2x - 3y + 5 = 2\cdot1 - 3\cdot2 + 5 = 2 - 6 + 5 = 1 \\
y' = x + 4y - 2 = 1 + 4 \cdot 2 -2 = 1 + 8 - 2 = 7
\end{cases} $$ Quindi, il punto $A(1,2) \mapsto A'(1,7)$
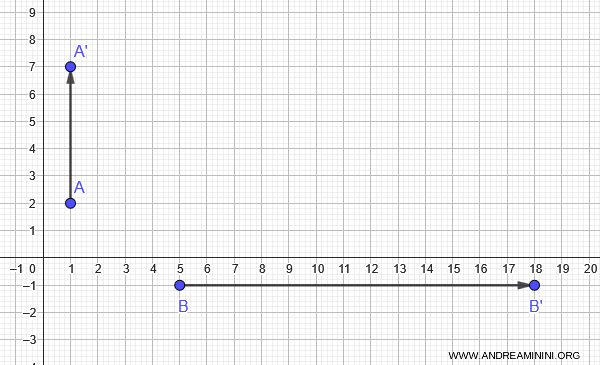
Ora considero il punto $B(5, -1)$ la cui trasformazione geometrica è $$
\begin{cases}
x' = 2x - 3y + 5 = 2\cdot5 - 3\cdot (-1) + 5 = 10 + 3 + 5 = 18 \\
y' = x + 4y - 2 = 5 + 4 \cdot (-1) -2 = 5 - 4 - 2 = -1 \end{cases} $$ Quindi, il punto $ B(5,-1) \mapsto B'(18, -1)$
Per trovare le equazioni del sistema inverso, ossia ricavare le variabili $x, y$ da $x', y'$, posso applicare Cramer o invertire la matrice:
$$
\begin{cases}
2x - 3y = x' - 5 \\
x + 4y = y' + 2
\end{cases}
$$
In questo caso utilizzo il metodo di Carmer sapendo che $ \Delta = 11 $
Nella matrice dei coefficienti sostituisco alla colonna delle $ x $ i termini noti per calcolare $ \Delta_x $
$$ \Delta_x = \begin{vmatrix} (x'-5) & -3 \\ y'+2 & 4 \end{vmatrix} $$
$$ \Delta_x = (x'-5) \cdot 4 - (y'+2) \cdot (-3) = 4x'-20 +3y' +6 $$
$$ \Delta_x = 4x' +3y' - 14 $$
Quindi, ricavo la variabile $ x' $
$$ x' = \frac{ \Delta_x }{ \Delta } = \frac{4x' +3y' - 14}{11} $$
Poi sostituisco alla colonna delle $ y $ i termini noti per calcolare $ \Delta_y $
$$ \Delta_y = \begin{vmatrix} 2 & (x'-5) \\ 1 & y'+2 \end{vmatrix} $$
$$ \Delta_y = 2 \cdot (y'+2) - (x'-5) \cdot 1 = 2y' + 4 - x' + 5$$
$$ \Delta_y = x' + 2y' + 9 $$
Quindi, ricavo la variabile $ y' $
$$ y' = \frac{ \Delta_y }{ \Delta } = \frac{y = x' + 2y' + 9}{11} $$
Quindi le equazioni inverse della trasformazione geometrica sono:
$$
\begin{cases}
x = \dfrac{3y' + 4x' - 14}{11} \\
y = \dfrac{2y' + 9 - x'}{11}
\end{cases}
$$
Questo conferma che da ogni punto trasformato si può tornare sempre indietro, quindi la biunivocità garantita.
Dal punto di vista grafico questo vuol dire che ogni punto del piano è connesso a un unico punto trasformato (immagine) e viceversa
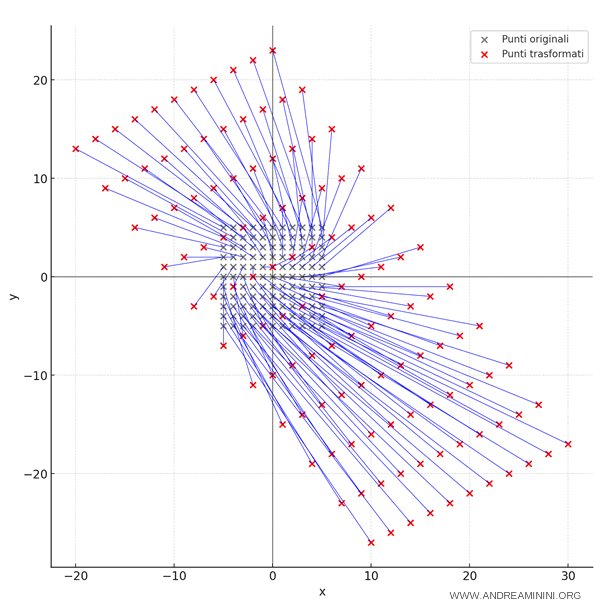
Nota. Posso ottenere le equazioni del sistema inverso anche usando la matrice inversa dei coefficienti. In questo esempio il sistema di equazioni lineari è:
$$
\begin{cases}
2x - 3y = x' - 5 \\
x + 4y = y' + 2
\end{cases}
$$
Riscrivo il sistema in forma matriciale
$$ A \cdot \vec{x} = \vec{b} $$
Dove $ A = \begin{pmatrix} 2 & -3 \\ 1 & 4 \end{pmatrix} $ è la matrice dei coefficienti, $ \vec{x} = \begin{pmatrix}
x \\ y \end{pmatrix} $ è il vettore delle incognite e $ \vec{b} = \begin{pmatrix} x' - 5 \\ y' + 2 \end{pmatrix} $ è quello dei termini noti.
$$
\begin{pmatrix}
2 & -3 \\
1 & 4
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=
\begin{pmatrix}
x' - 5 \\
y' + 2
\end{pmatrix}
$$
Pertanto, il vettore delle incognite $ \vec{x} $ posso ottenerlo in questo modo
$$ A \cdot \vec{x} = \vec{b} $$
$$ \vec{x} = \frac{1}{A} \cdot \vec{b} = A^{-1} \cdot \vec{b} $$
Dove $ A^{-1} $ è la matrice inversa dei coefficienti $ A $ e si calcola con la formula:
$$
A^{-1} = \frac{1}{\det(A)}
\begin{pmatrix}
\phantom{-}e & -b \\
-d & \phantom{-}a
\end{pmatrix} $$
$$ A^{-1} = \frac{1}{\det(A)}
\begin{pmatrix}
4 & 3 \\
-1 & 2
\end{pmatrix} $$
Il determinante della matrice dei coefficienti $ A $ è il seguente:
$$ \det(A) = \begin{vmatrix} 2 & -3 \\ 1 & 4 \end{vmatrix} = 2 \cdot 4 - (-3) \cdot 1 = 8 + 3 = 11 $$
Quindi, la matrice inversa è:
$$ A^{-1} = \frac{1}{11}
\begin{pmatrix}
4 & 3 \\
-1 & 2
\end{pmatrix} $$
A questo punto sostituisco la matrice inversa $ A^{-1} $ nell'equazione vettoriale
$$ \vec{x} = A^{-1} \cdot \vec{b} $$
$$ \vec{x} = \frac{1}{11} \begin{pmatrix} 4 & 3 \\ -1 & 2 \end{pmatrix} \cdot \vec{b} $$
Sapendo che $ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} $ e $ \vec{b} = \begin{pmatrix} x' - 5 \\ y' + 2 \end{pmatrix} $.
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \frac{1}{11} \begin{pmatrix} 4 & 3 \\ -1 & 2 \end{pmatrix} \begin{pmatrix} x' - 5 \\ y' + 2 \end{pmatrix} $$
Calcolo del primo termine $x$:
$$
x = \frac{1}{11} \left[ 4(x' - 5) + 3(y' + 2) \right]
= \frac{1}{11} (4x' - 20 + 3y' + 6)
= \frac{4x' + 3y' - 14}{11}
$$
Calcolo del secondo termine $y$:
$$
y = \frac{1}{11} \left[ -1(x' - 5) + 2(y' + 2) \right]
= \frac{1}{11} (-x' + 5 + 2y' + 4)
= \frac{-x' + 2y' + 9}{11}
$$
Quindi, le equazioni del sistema inverso sono le seguenti:
$$
\begin{cases}
x = \dfrac{4x' + 3y' - 14}{11} \\
y = \dfrac{-x' + 2y' + 9}{11}
\end{cases}
$$
E' lo stesso risultato ottenuto con il metodo di Cramer.
Come trovare la trasformazione geometrica di una funzione
Quando ho una funzione (es. una parabola: $y = x^2$) e voglio vedere che forma ha dopo una trasformazione geometrica, devo spostare i punti secondo certe regole.
- Trovo l'inversa della trasformazione \( t \), ossia riscrivo \( x \) e \( y \) in funzione di \( x' \) e \( y' \).
- Sostituisco le espressioni di \( x \) e \( y \) nell’equazione originale della funzione.
- Ottengo la nuova equazione, scritta nei nuovi assi \( x' \) e \( y' \).
Esempio
Parto dalla funzione:
$$ y = x^2 $$
E considero la trasformazione geometrica:
$$
t: \begin{cases}
x' = x + 1 \\
y' = y - 2
\end{cases}
$$
Per prima cosa, trovo l'inversa della trasformazione, ossia ricavo $ x $ e $ y $
$$
\begin{cases}
x' = x + 1 \Rightarrow x = x' - 1 \\
y' = y - 2 \Rightarrow y = y' + 2
\end{cases}
$$
Quindi l'inversa $t^{-1}$ è:
$$
t^{-1} : \begin{cases}
x = x' - 1 \\
y = y' + 2
\end{cases}
$$
Poi sostituisco $ x= x' - 1 $ e $ y= y' + 2 $ nell’equazione originale
$$ y = x^2 $$
$$ y' + 2 = (x' - 1)^2 $$
$$ y' + 2 = x'^2 - 2x' +1 $$
$$ y' = x'^2 - 2x' +1 - 2 $$
$$ y' = x'^2 - 2x' -1 $$
Quindi, la funzione $ y=x^2 $ dopo la trasformazione diventa $ y' = x'^2 - 2x' -1 $.
Questa trasformazione sposta i punti di 1 unità a destra (perché $x' = x + 1$) e di 2 unità in basso (perché $y' = y - 2$)
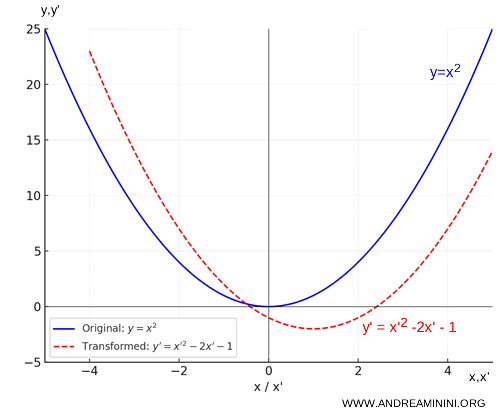
La parabola si sposta in basso a destra mantenendo la stessa forma.
Osservazioni
Alcune osservazioni e note a margine
- Le trasformazioni geometriche possono essere rappresentate matematicamente tramite equazioni, matrici, o funzioni. Ad esempio, una traslazione può essere espressa tramite l'aggiunta di un vettore costante a ogni punto, mentre una rotazione può essere rappresentata da una matrice di rotazione.
E così via
