Luogo geometrico

Un luogo geometrico è un insieme di punti che soddisfano una certa proprietà, regola o condizione.

La proprietà che caratterizza un luogo geometrico è detta prorietà caratteristica.

Per definire un luogo geometrico è necessario dimostrare che tutti i punti dell'insieme soddisfano la stessa regola e non esistono altri punti in grado di soddisfarla.

Un punto appartiene al luogo geometrico se è una delle soluzioni dell'equazione del luogo geometrico_.

A cosa serve? Il concetto di luogo geometrico costituisce una fondamentale base per la definizione di entità geometriche, curve e superfici, attraverso proprietà che possono essere rappresentate mediante equazioni algebriche.

Un esempio pratico

Dal punto di vista geometrico una retta è un insieme di punti allineati tra loro.

Quindi, la proprietà caratteristica della retta è l'allineamento dei punti sul piano.

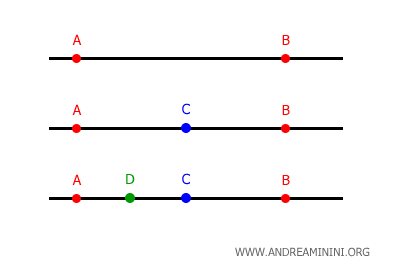
Per trovare i punti che appartengono alla retta devo cercare i valori delle variabili x e y che soddisfano l'equazione generale della retta

$$ ax+by+c = 0 $$

In questo caso, l'equazione generale della retta è l'equazione del luogo geometrico.

Esempio 2

L'asse di un segmento è l'insieme di punti equidistanti dagli estremi A e B del segmento.

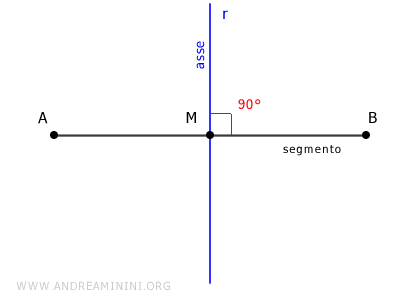
In questo caso la proprietà caratteristica è l'equidistanza dagli estremi del segmento $ \overline{PA} \cong \overline{PB} $ che implica, indirettamente, il passaggio dell'asse nel punto medio del segmento e la perpendicolarità (90°) rispetto al segmento.

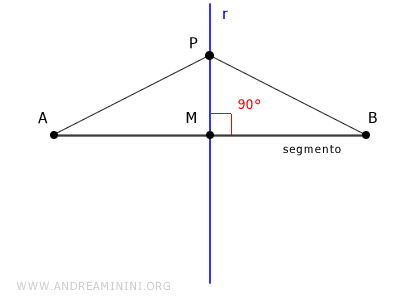
Quindi, l'equazione del luogo geometrico è l'equazione che eguaglia la distanza di un punto P(x;y) del piano dagli estremi A(x₁;y₁) e B(x₂;y₂) del segmento.

$ \underbrace{   \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $

Quest'ultima equazione identifica tutti i punti equidistanti dagli estremi del segmento AB, ovvero tutti i punti dell'asse del segmento.

Spiegazione. In quest'ultima equazione misuro le distanze AP e BP utilizzando il teorema di Pitagora sui triangoli AMP e BMP. $$ \overline{AP} = \overline{BP} $$ $$ \underbrace{ \sqrt{ \overline{MP}^2 + \overline{AM}^2 } }_{AP} =  \underbrace{ \sqrt{ \overline{MP}^2 + \overline{BM}^2 } }_{BP} $$

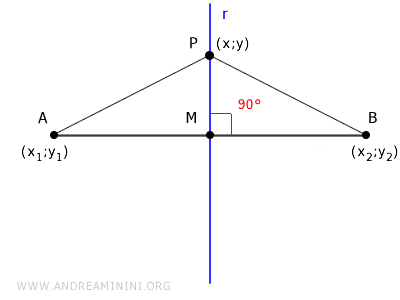
Sapendo che MP=|y-y₁|=|y-y₂|, AM=|x-x₁| e BM=|x-x₂| ottengo l'equazione dell'equidistanza dei punti dagli estremi del segmento $$ \underbrace{   \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $$

Altri esempi di luoghi geometrici

• Una circonferenza è il luogo geometrico dei punti in un piano che sono a una distanza fissa da un punto P detto "centro".
• La bisettrice di un angolo è il luogo geometrico dei punti equidistanti dai lati di un angolo.
• La parabola è il luogo geometrico dei punti in un piano che sono equidistanti da un punto fisso (detto fuoco) e da una retta fissa (detta direttrice) è una parabola.
• L'ellise è il luogo geometrico dei punti per cui la somma delle distanze da due punti fissi (detti fuochi) è costante è un'ellisse.
• L'iperbole è il luogo geometrico dei punti per cui la differenza delle distanze da due punti fissi (detti fuochi) è costante è un'iperbole.

E così via.