Area

L'area in geometria misura l'estensione di una superficie su un piano. Può essere definita anche come la quantità di spazio all'interno del perimetro di una figura del piano.

E' un concetto geometrico che si applica alle figure bidimensionali ovvero che hanno due dimensioni.

L'area è una grandezza scalare rappresentata da un numero reale non negativo che descrive la dimensione di una regione o di una figura all'interno di un piano.

Il numero indica quante volte l'unità di misura scelta per misurare l'area è contenuta nella superficie considerata.

L'unità di misura standard per l'area è il metro quadrato (m² o mq), sebbene possano essere utilizzate anche i multipli e i sottomultipli, come centimetri quadrati (cm²), chilometri quadrati (km²).

A seconda del contesto, l'area può essere misurata anche con altre unità di misura come i pollici quadrati, l'ettaro quadrato (ha) usato in agricoltura che equivale a 10mila mq, ecc.

Nota. Il concetto di area è stato studiato fin dall'antichità. Matematici greci come Euclide e Archimede hanno elaborato le prime teorie sistematiche sull'area, inclusi metodi per il calcolo dell'area di vari poligoni e cerchi. E' un concetto utilizzato in numerosi campi oltre la matematica pura, come l'architettura, l'ingegneria civile, l'agricoltura e la geografia. È fondamentale nella pianificazione di spazi.

L'area in fisica

L'area è una grandezza fisica derivata che misura l'estensione di una superficie piana.

E' una grandezza "derivata" perché deriva dall'utilizzo di una grandezza fondamentale: la lunghezza (L).

La sua unità di misura standard nel Sistema Internazionale è il metro quadrato (m²). Questa unità indica l'area occupata da un quadrato i cui lati misurano 1 metro.

Dal punto di vista dell'analisi dimensionale l'area è il prodotto tra due lunghezze che definisco la larghezza e l'altezza di una figura elementare.

$$ \text{Area} = [L] \cdot [L] $$

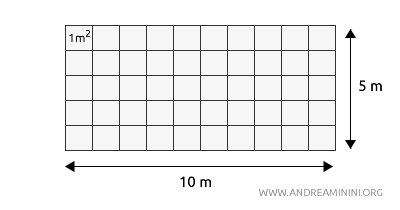
Il calcolo dell'area di figure piane, come un rettangolo, si effettua moltiplicando la lunghezza della base per quella dell'altezza.

Ad esempio, per un rettangolo con base di 10 metri e altezza di 5 metri:

$$ \text{Area} = \text{base} \times \text{altezza} = (10 \, \text{m}) \times (5 \, \text{m}) = 50 \, \text{m}^2 $$

Questa operazione mostra non solo il calcolo numerico ($10 \times 5 = 50$), ma anche l’importanza di moltiplicare le unità ($m \times m = m^2$).

Così, l'area rappresenta il numero di quadrati di lato 1 metro che posso disporre sulla superficie del rettangolo.

Il calcolo dell'area

Il calcolo dell'area varia a seconda della figura:

• Area del triangolo
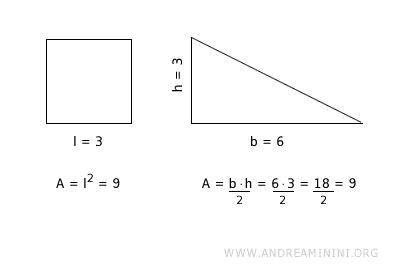
  L'area di un triangolo si calcola dividendo per due il prodotto tra la base e l'altezza. $$ A = \frac{Base \ × \ Altezza }{2} $$
• Area del quadrato
  L'area di un quadrato si ottiene calcolando il quadrato di un lato $$ A = lato \ × \ lato = lato ^2 $$
• Area del quadrato, rettangolo, parallelogramma
  L'area di un quadrato, rettangolo o parallelogramma si calcola moltiplicando la base e l'altezza. $$ A = Base \ × \ Altezza $$
• Area del rombo
  L'area del rombo è uguale al prodotto tra le diagonali d₁ e d₂ diviso due. $$ A = \frac{d_1 \ × \ d_2 }{2} $$
• Area del trapezio
  L'area del trapezio è uguale al semiprodotto tra l'altezza e la somma della base maggiore (Base) e della base minore (base) $$ A = \frac{(Base + base) }{2} \ × \ Altezza $$
• Area del cerchio
  L'area del cerchio si calcola moltiplicando il quadrato del raggio del cerchio per la costante pi greco ( π=3.14... ). $$ A = \pi r^2 $$
• Area dei poligoni regolari
  L'area di un poligono regolare si calcola moltiplicando il perimetro per l'apotema diviso due. $$ A = \frac{Perimetro \ × \ Apotema }{2} $$
• Area delle figure irregolari
  L'area di una figura irregolare richiede la suddivisione in forme più semplici oppure metodi di integrazione.
  

  

   

I multipli e sottomultipli del metro quadro

Nel sistema metrico decimale l'unità di misura dell'area è il metro quadrato (mq o m^2) che corrisponde a un quadrato che ha ogni lato lungo 1 metro.

I multipli e i sottomultipli del metro quadro sono:

mm2	millimetri quadri
cm2	centimetri quadri
dm2	decimetri quadri
m2	metri quadri
dam2	decametri quadri
hm2	ettometri quadri
km2	chilometri quadri

Ogni unità vale 100 volte l'unità immediatamente inferiore e la centesima parte di quella superiore.

Ad esempio, il metro quadro m² equivale a 100 dm² e a un 1/100 dam².

Conversione delle unità di misura dell'area

L'area può essere espressa anche in termini di multipli e sottomultipli del metro quadrato. Ad esempio, posso usare:

• Centimetro quadrato ($cm^2$): corrisponde a $10^{-4}$ metri quadrati.
• Millimetro quadrato ($mm^2$): corrisponde a $10^{-6}$ metri quadrati.
• Chilometro quadrato ($km^2$): corrisponde a $10^6$ metri quadrati.

Questi fattori di conversione sono cruciali.

Ad esempio, per passare da $m^2$ a $cm^2$, si moltiplica per $10^4$ poiché $1 \, cm = 10^{-2} \, m$. Di conseguenza:

$$ 1 \, cm^2 = (10^{-2} \, m) \times (10^{-2} \, m) = 10^{-4} \, m^2 $$

Questo stesso principio si applica anche ad altre conversioni, come quella dal millimetro quadrato al metro quadrato:

$$ 1 \, mm^2 = (10^{-3} \, m) \times (10^{-3} \, m) = 10^{-6} \, m^2 $$

E per il chilometro quadrato:

$$ 1 \, km^2 = (10^3 \, m) \times (10^3 \, m) = 10^6 \, m^2 $$

In generale, quando si converte l'unità di misura dell'area è importante applicare il quadrato del fattore di conversione.

Ad esempio, ho una superficie di 100 m2 e voglio convertire la misura in decimetri quadri (dm²). Per farlo non devo moltiplicare semplicemente per 10, come farei nel caso di una lunghezza, bensì devo moltiplicare per il quadrato di 10 ossia per 10². $$ 100 \ m^2 = 100 \cdot 10^2 \ dm^2 = 10000 \ dm^2 $$ Se voglio ottenere la misura in centimetri quadri (cm²) devo considerare il quadrato di 10². $$ 100 \ m^2 = 100 \cdot (10^2)^2 \ cm^2 = 100 \cdot 10^4 \ cm^2 = 10^6 \ cm^2 $$ Per ottenere la misura in millimetri quadri (mm²) devo usare il quadrato di 10³. $$ 100 \ m^2 = 100 \cdot (10^3)^2 \ mm^2 = 100 \cdot 10^6 \ cm^2 = 10^8 \ mm^2 $$ E via dicendo.

Le classi di equivalenza dell'area

Due figure geometriche appartengono alla stessa classe di equivalenza se hanno la stessa area,

L'area delle figure geometriche forma delle classi di equivalenza,

I poligoni che hanno la stessa area appartengono alla stessa classe di equivalenza sono anche detti poligoni equivalenti.

E così via.