I postulati di Euclide

Euclide, nel suo opera fondamentale "Gli Elementi", ha formulato cinque postulati che costituiscono le basi della geometria euclidea.

I cinque postulati di Euclide sono affermazioni matematiche fondamentali che si presuppone siano vere senza necessità di dimostrazione.

Questi postulati formano la base della geometria piana, che è comunemente insegnata nelle scuole.

Nota. Se si decidesse di rifiutare anche solo uno di questi postulati di Euclide, si verrebbe a creare un tipo di geometria diverso, noto come geometria non euclidea.

Questi postulati sono:

Primo postulato

Tra due punti distinti qualsiasi passa una e una sola retta.

Questa affermazione implica la presenza di una condizione di esistenza e di unicità, perché tra due punti diversi esiste una retta (esistenza) e questa retta è unica (unicità).

Corollari

Dagli assiomi si deducono anche altri corollari

• Per un punto passano infinite rette.
• Su una retta ci sono almeno due punti.
• In tre punti non allineati passa un solo piano.
• In tre punti allineati passa una e una sola retta .
• In una retta passano infiniti piani.

Secondo postulato

È possibile estendere all'infinito un segmento di linea in una linea retta continua.

Terzo postulato

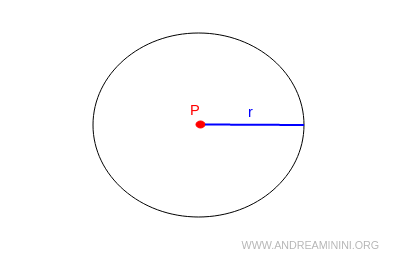
Dato un punto e un segmento di lunghezza qualsiasi è possibile disegnare un cerchio.

Quarto postulato

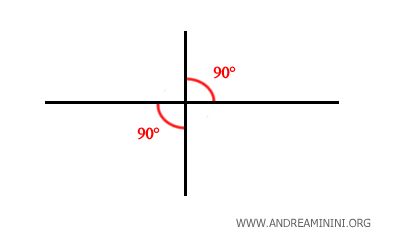
Tutti gli angoli retti sono congruenti tra loro, cioè hanno la stessa misura.

Quinto postulato

Se una linea retta "r" interseca due altre linee rette "s" e "t" formando angoli interni α e β sullo stesso lato, la cui somma α+β<180° è inferiore a due angoli retti, allora le due linee "s" e "t" , se prolungate all'infinito, si incontreranno in un punto P.

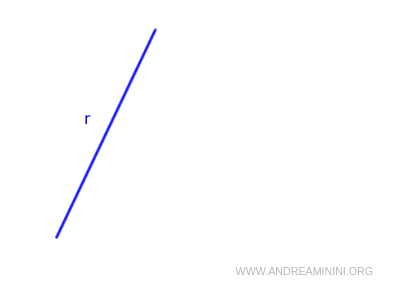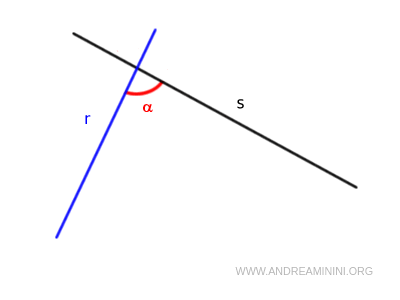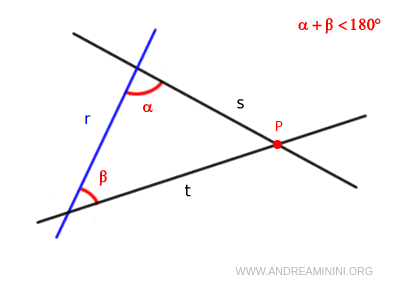
Il quinto postulato di Euclide è conosciuto anche come "postulato delle parallele".

Questo perché se una retta interseca due rette che formano una somma di due angoli interni di 180°, allora le due rette sono parallele tra loro e non si intersecano mai sul piano.

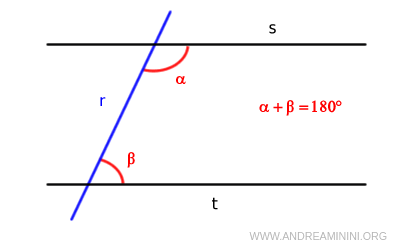
Nel corso del tempo sono state scritte diverse formulazioni di questo postulato.

Nota. Il V postulato di Euclide è stato oggetto di numerosi dibattiti e analisi nel corso dei secoli. Per più di duemila anni, i matematici hanno cercato di ricondurre questo postulato agli altri quattro postulati, ma non ci sono riusciti. Infine, nel XIX secolo, hanno dimostrato che non è possibile farlo. Se si cambia il quinto postulato, otteniamo un tipo di geometria completamente diverso dalla geometria euclidea, chiamato "geometria non euclidea". Esistono diversi tipi di geometrie non euclidee. Ad esempio, la geometria sferica, la geometria iperbolica, la geometria ellittica, ecc.

E così via