Spazio in geometria

Lo spazio è un ente fondamentale della geometria. E' composto da infiniti piani e, in senso generale, rappresenta il "contenitore" in cui si rappresentano le figure solide.

Nella geometria euclidea si parla di "spazio" per intendere lo spazio su tre dimensioni (x,y,z), lo specifico perché in matematica lo spazio può anche avere anche più dimensioni.

Ogni figura geometrica solida (es. cubo, parallelepipedo, sfera, ecc.) posso vederla come un insieme di punti che appartengono a piani diversi.

La geometria che si occupa dello spazio è anche detta geometria dei solidi.

Nota. In generale, le figure geometriche solide sono oggetti tridimensionali che permettono di studiare non solo la forma, ma anche le proprietà geometriche e fisiche delle strutture. Si distinguono dalle figure geometriche piane che, invece, possono essere studiate solo nella forma, essendo degli oggetti su due dimensioni.

Nella geometria euclidea, lo spazio è tradizionalmente descritto utilizzando coordinate cartesiane (x,y,z) che definiscono le posizioni dei punti in tre dimensioni: lunghezza, larghezza e altezza.

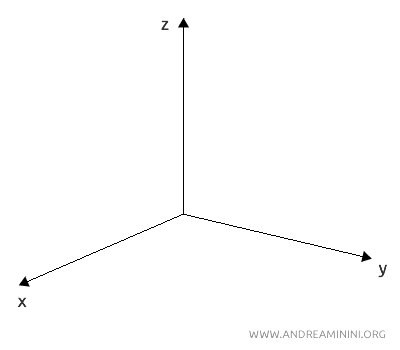
Ad esempio, il cubo è una figura solida con sei facce quadrate che può essere rappresentata con coordinate che identificano i vertici nello spazio.

I suoi punti appartengono a diversi piani che si intersecano formando angoli retti.

 

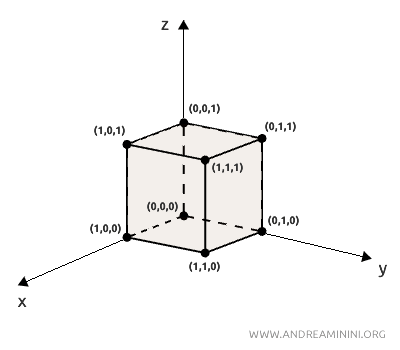
Se volessi posizionarlo in un sistema cartesiano, potrei definire i suoi vertici con coordinate tridimensionali come (0, 0, 0), (0, 1, 0), (1, 1, 0) e così via.

I piani nello spazio

Lo spazio è composto da infiniti piani che possono avere solo due tipi di relazioni tra loro:

• Piani paralleli
  Non hanno alcun punto in comune e sono equidistanti in ogni loro parte. Un esempio pratico sono i pavimenti di due piani di un edificio: se non ci sono deformazioni, si trovano su piani paralleli.
  
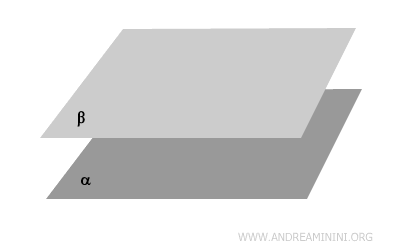
• Piani incidenti
  Quando due piani non sono paralleli, si dice che sono incidenti. In tal caso, i due piani si intersecano lungo una retta.
  

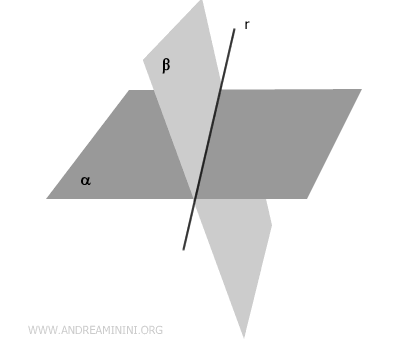
Dal punto di vista teorico, due piani non possono intersecarsi in un solo punto nello spazio tridimensionale, poiché una loro eventuale intersezione deve formare una retta (dimostrazione).

La proprietà di parallelismo tra due piani gode delle seguenti proprietà:

• Riflessiva
  Ogni piano è parallelo a se stesso
• Simmetrica
  Se un piano A è parallelo al piano B, allora anche il piano B è parallelo al piano A
• Transitiva
  Se un piano A è parallelo al piano B e B è parallelo al piano C, allora il piano A è parallelo a C.

La posizione di una retta rispetto a un piano nello spazio tridimensionale può essere descritta con precisione in base ai seguenti tre casi principali:

• Retta complanare o giacente sul piano
  La retta si trova interamente sul piano, il che significa che ogni punto della retta appartiene al piano stesso.
  
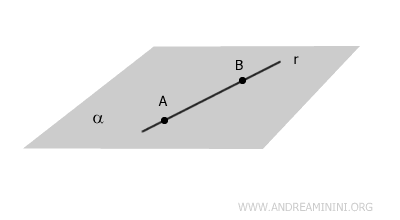
• Retta incidente al piano
  In questo caso, la retta ha un solo punto P in comune con il piano, ossia interseca il piano in un punto specifico.
  
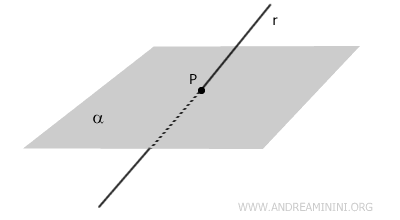
• Retta parallela al piano
  La retta non ha punti in comune con il piano.
  

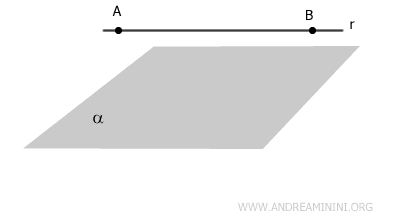
Queste relazioni sono essenziali per comprendere la geometria tridimensionale.

I postulati dello spazio

In geometria i principali postulati dello spazio sono i seguenti:

• Per tre punti distinti e non allineati dello spazio passa uno e un solo piano.
  
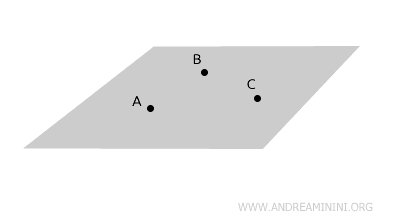
• Per due punti distinti di un piano, la retta che passa per i due punti giace interamente sullo stesso piano.
  
• Postulato di partizione dello spazio
  Un piano divide i punti dello spazio che non appartengono al piano in due regioni, dette semispazi. Il piano è detto origine dei semispazi.
  
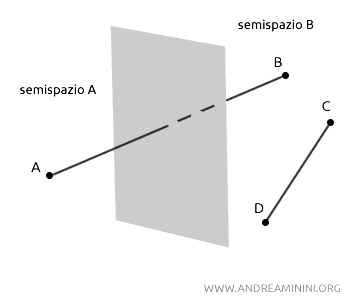
  Dati due punti qualsiasi A e B presi in semispazi diversi, gli estremi del segmento AB intersecano il piano. Dati due punti qualsiasi C e D nello stesso semispazio, gli estremi del segmento CD non intersecano il piano.

Le rette nello spazio

Le rette nello spazio possono risiedere sullo stesso piano o giacere su piani diversi.

Due rette che giacciono sullo stesso piano sono dette rette complanari e possono essere incidenti o parallele, a seconda se hanno un solo punto in comune oppure no.

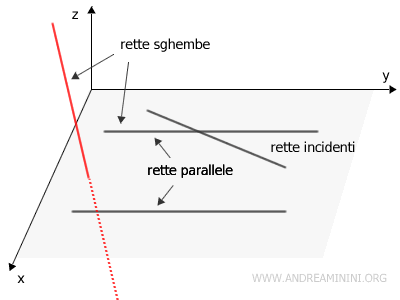
Le rette che si trovano su piani diversi sono dette rette sghembe e non hanno punti in comune.

Perché le rette sghembe non hanno un punto in comune? Le rette sghembe non hanno un punto in comune perché, per definizione, esse non giacciono nello stesso piano. Considero per assurdo che due rette sghembe r₁ e r₂ abbiano un punto P in comune.

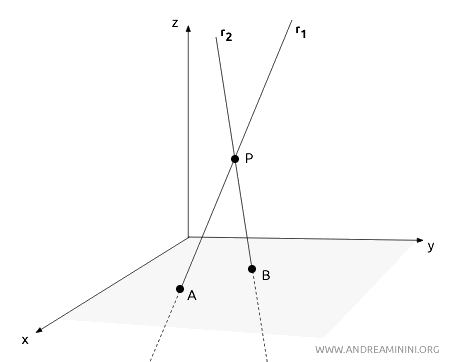
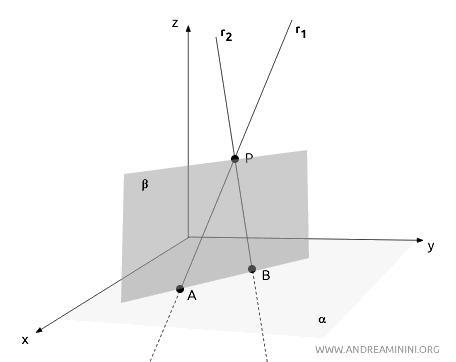
In questo caso, potrei scegliere un altro punto A su una delle rette e un punto B sull'altra retta, entrambi distinti da P. Con questi tre punti P, A, e B, è possibile definire un piano unico β che contiene entrambe le rette. Questo implicherebbe che le rette siano complanari. Tuttavia, l'essenza delle rette sghembe è proprio quella di essere non complanari. Dunque, se due rette sono incidenti, necessariamente appartengono allo stesso piano e quindi non possono essere sghembe. 

Note a margine

Alcune note aggiuntive sullo spazio in geometria

• Lo spazio in fisica
  In fisica lo spazio è un elemento fondamentale nella teoria della relatività. Albert Einstein, nella sua teoria dello spazio-tempo, ha descritto lo spazio non come un'entità fissa, ma come qualcosa di relativo e interdipendente con il tempo.  Questo concetto è detto "spazio-tempo" e porta a fenomeni come la dilatazione del tempo o la contrazione dello spazio in presenza di velocità elevate o campi gravitazionali intensi. Tutte queste considerazioni, però, non sono prese in considerazione quando si parla di spazio geometrico.

E così via.