Il teorema del coseno
Il quadrato di un lato del triangolo b2 è uguale alla somma dei quadrati degli altri due lati a2+c2, meno il doppio prodotto dei due lati 2ac per il coseno dell'angolo α tra i due lati. $$ b^2 = a^2 + c^2 - 2ac \cdot \cos \alpha $$
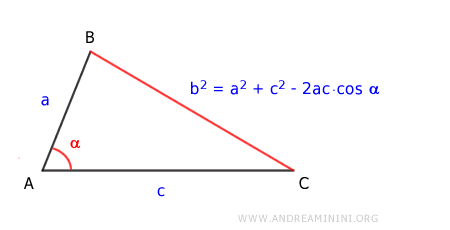
Questo teorema è anche conosciuto come teorema del coseno di Carnot.
Esempio
Devo calcolare la lunghezza del lato BC di questo triangolo
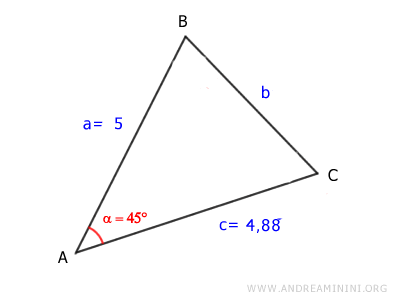
Del triangolo conosco la lunghezza dei lati AB e AC e l'ampiezza dell'angolo α
$$ \overline{AB} = 5 $$
$$ \overline{AC} = 4,88 $$
$$ \alpha =45° $$
Applico il teorema del coseno sul lato BC
$$ \overline{BC}^2 = \overline{AB}^2 + \overline{AC}^2 -2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$
Sapendo che AB=5, AC=4,88 e α=45°
$$ \overline{BC}^2 = 5^2 + (4,88)^2 -2 \cdot (5 \cdot 4,88) \cdot \cos 45° $$
$$ \overline{BC}^2 = 14,3 $$
Calcolo la matrice quadrata in entrambi i membri dell'equazione
$$ \sqrt{ \overline{BC}^2 } = \sqrt{ 14,3 } $$
$$ \overline{BC} = \sqrt{ 14,3 } $$
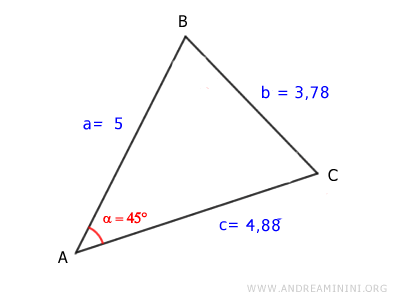
$$ \overline{BC} = 3,78 $$
Il lato BC misura 3,78
La dimostrazione
Considero un triangolo ABC qualsiasi.
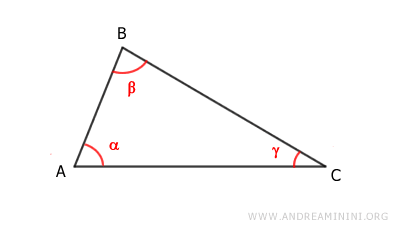
Traccio l'altezza h del triangolo ottenendo due triangoli rettangoli ABD e BCD.
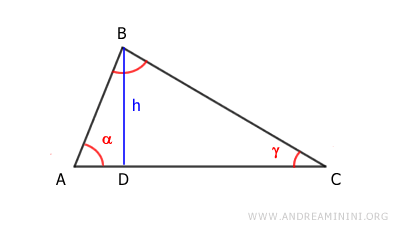
Secondo il primo teorema del triangolo rettangolo in base al quale un cateto è uguale all'ipotenusa per il coseno dell'angolo adiacente al cateto oppure per il seno dell'angolo opposto.
In questo modo ottengo la lunghezza dei lati BD e AD
$$ \overline{BD} = \overline{AB} \cdot \sin \alpha $$
$$ \overline{AD} = \overline{AB} \cdot \cos \alpha $$
Dove AB è l'ipotenusa del triangolo rettangolo ABD mentre BD e AD sono i cateti.
Sapendo che il segmento AC è la somma dei segmenti AD e CD
$$ \overline{AC} = \overline{AD} + \overline{CD} $$
ottengo per differenza il cateto CD del triangolo BCD
$$ \overline{CD} = \overline{AC} - \overline{AD} $$
$$ \overline{CD} = \overline{AC} - \overline{AB} \cdot \cos \alpha $$
Secondo il teorema di Pitagora il quadrato dell'ipotenusa BC è uguale alla somma dei quadrati dei cateti del triangolo rettangolo BCD.
$$ \overline{BC}^2 = \overline{BD}^2 + \overline{CD}^2 $$
Sapendo che CD=AC-AB·cos α
$$ \overline{BC}^2 = \overline{BD}^2 + (\overline{AC} - \overline{AB} \cdot \cos \alpha )^2 $$
e che BD=AB·sin α
$$ \overline{BC}^2 = (\overline{AB} \cdot \sin \alpha)^2 + (\overline{AC} - \overline{AB} \cdot \cos \alpha )^2 $$
$$ \overline{BC}^2 = \overline{AB}^2 \cdot \sin^2 \alpha + \overline{AC}^2 -2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha + \overline{AB}^2 \cdot \cos^2 \alpha$$
$$ \overline{BC}^2 = \overline{AB}^2 \cdot ( \sin^2 \alpha + \cos^2 \alpha) + \overline{AC}^2 -2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$
Per la prima relazione fondamentale della trigonometria sin2 α +cos2 α = 1
$$ \overline{BC}^2 = \overline{AB}^2 \cdot ( 1 ) + \overline{AC}^2 -2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$
$$ \overline{BC}^2 = \overline{AB}^2 + \overline{AC}^2 -2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$
Il risultato è la formula che volevo dimostrare.

ossia

Nota. Quando il triangolo è un triangolo rettangolo il teorema del coseno si riduce al teorema di Pitagora perché l'angolo alfa in un triangolo rettangolo ha ampiezza 90° e il coseno di 90° è uguale a zero. $$ a^2 = b^2 + c^2 - 2bc \cdot \cos \alpha $$ $$ a^2 = b^2 + c^2 - 2bc \cdot \cos 90° $$ $$ a^2 = b^2 + c^2 - 2bc \cdot 0 $$ $$ a^2 = b^2 + c^2 $$
E così via.
