Il teorema dell'asse di una corda
In una circonferenza l’asse di una corda passa sempre per il centro della circonferenza.
La dimostrazione
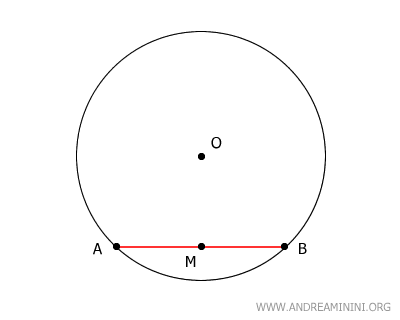
Considero una corda AB e il punto medio M della corda.
Congiungo gli estremi A e B della corda al centro O tramite i segmenti OA o OB, formando così il triangolo ABO.
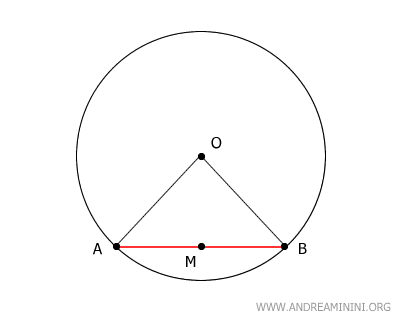
I segmenti OA e OB sono congruenti perché sono due raggi della circonferenza.
$$ \overline{OA} \cong \overline{OB} $$
Il triangolo ABO ha due lati congruenti OA≅OB, quindi è un triangolo isoscele.
Nei triangoli isosceli la mediana tracciata dal vertice O verso il punto medio M sul lato opposto AB coincide con l'altezza, la bisettrice e l'asse.

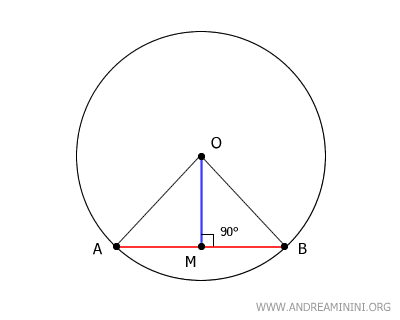
In questo caso, il segmento OM è la mediana e, contemporaneamente, anche l'altezza del triangolo. Pertanto, OM è perpendicolare ad AB, formando un angolo di 90°.
Il segmento OM è anche l'asse del segmento AB perché è perpendicolare (90°) e passa per il punto medio M del segmento.

Per costruzione, uno degli estremi del segmento OM è il centro O della circonferenza.
Questo dimostra che l'asse di una corda passa sempre per il centro della circonferenza.
E così via
