Area di un poligono irregolare
Il calcolo dell'area di un poligono irregolare e di qualsiasi figura piana è un po' più complicato rispetto ai poligoni regolari. Tuttavia, ci sono diversi metodi per farlo, a seconda delle informazioni disponibili e della natura del poligono. Ecco alcune tecniche comuni:
La decomposizione in poligoni regolari
Una figura piana può essere suddivisa in forme più semplici come triangoli, rettangoli, trapezi, ecc.
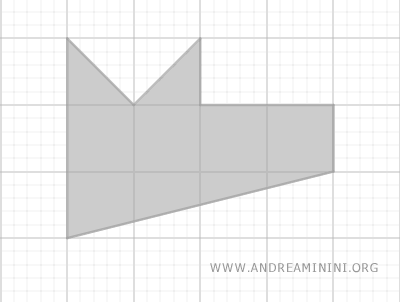
L'area del poligono irregolare si trova sommando le aree dei poligoni regolari che lo formano.
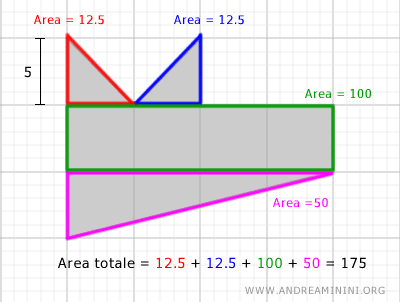
Quando una figura, o una parte della figura, non può essere suddivisa in un poligono regolare, posso calcolare una stima.
Ad esempio, considero questa figura curvilinea.
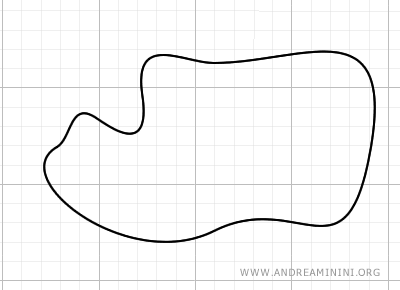
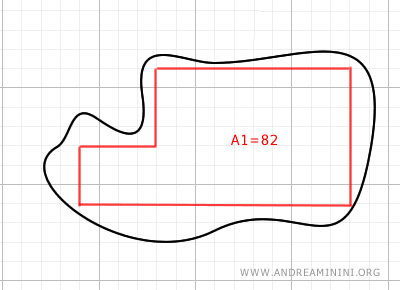
Per stimare l'area disegno una poligonale inscritta dentro la figura, cercando di ridurre al minimo gli spazi vuoti.
Quindi, suddivido l'area in poligoni regolari, calcolo l'area per ciascuno di essi e le sommo.
In questo modo ottengo l'area A1=82 della poligonale inscritta.
Ora disegno una poligonale circoscritta all'esterno della figura curvlinea, cercando di ridurre al minimo gli spazi vuoti.
Poi calcolo suddivido la poligonale in poligoni regolari, calcolo l'area di ciascun poligono e le sommo.
In questo modo ottengo l'area A2 della poligonale circoscritta.
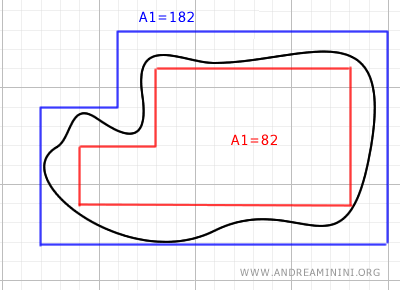
A questo punto, posso affermare che l'area della figura irregolare è compresa tra l'area della poligonale inscritta A1=82 e l'area della poligonale circoscritta A2=182.
$$ A_1 < A < A_2 $$
$$ 85 < A < 182 $$
Infine, calcolo la media di questi due valori approssimativi.
$$ A = \frac{A_1+A_2}{2} $$
$$ A = \frac{82+182}{2} $$
$$ A = \frac{264}{2} $$
$$ A = 132 $$
L'area della figura piana è approssimativamente composta da 132 quadratini.
In questo modo posso ottenere una stima approssimativa dell'area di qualsiasi figura piana.
Nota. Ovviamente si tratta di una stima. La precisione della stima dipende dalla granularità con cui suddivido la figura piana. Più piccoli sono i poligoni regolari utilizzati per approssimare l'area, maggiore sarà la precisione della stima.
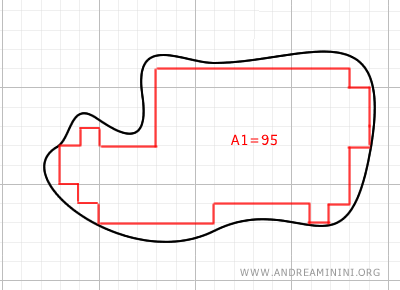
Questo metodo di calcolo approssimativo viene sviluppato nell'analisi matematica ed è alla base degli integrali definiti di Riemann.
Formula shoelace (o formula di Gauss)
Questa formula è utile se conosco le coordinate dei vertici del poligono irregolare. Supponendo che il poligono abbia vertici (x1,y1),(x2,y2),…,(xn,yn) e che (xn+1,yn+1)=(x1,y1), l'area A del poligono è data dalla seguente sommatoria
$$ A= \frac{1}{2} \cdot | \sum_i^n ( x_i y_{i+1} - x_{i+1} y_i ) | $$
Ad esempio, considero questo poligono irregolare.
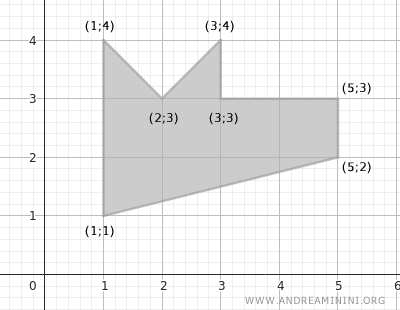
Le coordinate del poligono sono
$$ (x_1;y_1) = (1;1) \\ (x_2;y_2) = (1;4) \\ (x_3;y_3) = (2;3) \\ (x_4;y_4) = (3;4) \\ (x_5;y_5) = (3;3) \\ (x_6;y_6) = (5;3) \\ (x_7;y_7) = (5;2) $$
Poiché la poligonale deve essere chiusa, aggiungo un ulteriore coordinata che coincide con quello iniziale
$$ (x_8;y_8) = (5;2) $$
Ora applico la formula per calcolare la sommatoria
$$ A= \frac{1}{2} \cdot | \sum_1^7 ( x_i y_{i+1} - x_{i+1} y_i ) | $$
$$ A= \frac{1}{2} \cdot | (x_1 y_2 - x_2 y_1) + (x_2 y_3 - x_3 y_2) + (x_3 y_4 - x_4 y_3) + \\ \ \ \ \ + (x_4 y_5 - x_5 y_4) + (x_5 y_6 - x_6 y_5) + (x_6 y_7 - x_7 y_6) + (x_7 y_8 - x_8 y_7) | $$
Sostituisco i valori delle coordinate x1=1, x2=1, x3=2, x4=3, x5=3, x6=5, x7=5, x8=1 e
$$ A= \frac{1}{2} \cdot | (1 \cdot y_2 - 1 \cdot y_1 + (1 \cdot y_3 - 2 \cdot y_2) + (2 \cdot y_4 - 3 \cdot y_3) + \\ \ \ \ \ + (3 \cdot y_5 - 3 \cdot y_4) + (3 \cdot y_6 - 5 \cdot y_5) + ( 5 \cdot y_7 - 5 \cdot y_6) + (5 \cdot y_8 - 1 \cdot y_7) | $$
Sostituisco i valori delle coordinate y1=1, y2=4, y3=3, y4=4, y5=3, y6=3, y7=2, y8=1
$$ A= \frac{1}{2} \cdot | (1 \cdot 4 - 1 \cdot 1 + (1 \cdot 3 - 2 \cdot 4) + (2 \cdot 4 - 3 \cdot 3) + \\ \ \ \ \ + (3 \cdot 3 - 3 \cdot 4) + (3 \cdot 3 - 5 \cdot 3) + ( 5 \cdot 2 - 5 \cdot 3) + (5 \cdot 1 - 1 \cdot2) | $$
Quindi svolgo i calcoli
$$ A= \frac{1}{2} \cdot | (4 - 1) + (3 - 8) + (8 - 9) + (9 - 12) + (9 - 15) + ( 10 - 15) + (5 - 2) | $$
$$ A= \frac{1}{2} \cdot | 3 -5 -1 -3 -6 -5+3 | $$
$$ A= \frac{1}{2} \cdot | -14 | $$
$$ A= \frac{1}{2} \cdot 14 $$
$$ A= 7 $$
Poiché ogni quadrato è composto da 5x5=25 quadratini
L'area del poligono irregolare è 25·7 ossia 175 quadratini
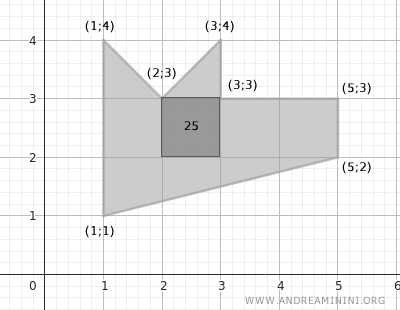
E' lo stesso risultato ottenuto precedentemente.
E così via
