I polinomi
Cosa sono i polinomi
Un polinomio è una somma algebrica di monomi.
Ecco un esempio pratico di polinomio
$$ a^2c + bc + abc $$
Quest'ultimo polinomio è composto dalla somma algebrica di tre monomi.
Cosa significa polinomio? Si chiama "polinomio" perché deriva dal greco "poli" (molto) e dal latino "nomen" (termini). Quindi, significa "molti termini".
I monomi che formano il polinomio sono detti termini del polinomio. Ogni termine ha un coefficiente.
Ad esempio, questo polinomio ha due termini, il coefficiente del primo termine è 3, quello del secondo termine è 1 che in un monomio è implicito e non va scritto.
$$ 3a + ab $$
Se nel polinomio è presente un termine numerico diverso da zero, si dice termine noto del polinomio.
Ad esempio, in questo polinomio il termine noto è 3.
$$ 4a + 2ab + \color{red}3 $$
A seconda del numero di termini, un polinomio in forma normale è detto monomio (1 termine), binomio (2 termini), trinomio (3 termini), quadrinomio (4 termini).
Ad esempio, questo polinomio è un binomio perché è composto da due termini.
$$ ab + 3bc $$
Quest'altro polinomio, invece, è un trinomio perché è composto solo da tre termini
$$ ab + 3bc + c $$
Quando un polinomio è in forma normale? Un polinomio è in forma normale quando è composto da monomi diversi, ovvero quando non ci sono monomi simili al suo interno. Nel paragrafo seguente lo spiego in modo più dettagliato facendo qualche esempio pratico.
I polinomi in forma normale
Un polinomio è in forma normale (o polinomio ridotto) quando tutti i termini sono in forma normale e non è composto da monomi simili.
Ad esempio, questo è un polinomio in forma normale perché è composto da monomi differenti. Non ci sono monomi simili.
$$ 3ab^2 + 5ab + c $$
Quest'altro polinomio, invece, non è in forma normale perché contiene due monomi simili (2ab e 3ab)
$$ 3ab^2 + 2ab + 3ab + c $$
Come ridurre un polinomio in forma normale
Qualsiasi polinomio può essere ridotto in forma normale facendo la somma algebrica dei monomi simili al suo interno.
Esempio
Considero questo polinomio non in forma normale
$$ 3ab^2 + 2ab + 3ab + c $$
Al suo interno ci sono due monomi simili (2ab e 3ab)
Utilizzo la proprietà distributiva per sommare i due monomi simili
$$ 3ab^2 + (2+3) \cdot ab + c $$
$$ 3ab^2 + 5 ab + c $$
Il risultato è lo stesso polinomio ridotto in forma normale.
Il grado di un polinomio
Il grado di un polinomio in forma normale è il grado maggiore dei termini.
Esempio
In questo polinomio il primo termine (a3b) è di grado 4, il secondo termine (ab2) e il terzo termine (abc) sono di grado 3
$$ a^3b + ab^2 + abc $$
Quindi, il polinomio è di grado 4.
Nota. Il grado di un polinomio deve essere calcolato soltanto nei polinomi in forma normale. Pertanto, se un polinomio non è in forma normale va prima ridotto.
Il grado di un polinomio rispetto a una lettera è l'esponente più alto (grado maggiore) di un letterale nel polinomio.
Esempio
Questo polinomio è composto dalle lettere a, b, c
$$ a^3b + ab^2 + abc + 5 $$
Il grado del polinomio è 3 rispetto alla lettera "a", è 2 rispetto alla lettera "b" e, infine, è 1 rispetto alla lettera "c".
Il termine noto
Il termine di grado zero in un polinomio è detto termine noto.
Ad esempio, in questo polinomio il termine di grado zero (termine noto) è 5
$$ ab^3 + a^2bc + ab + 5 $$
Spiegazione. Hanno grado zero tutti i numeri del polinomio non moltiplicati a una lettera. Sapendo che l'elevazione di una qualsiasi lettera a zero è uguale a uno (es. a0=1) per convenzione, un numero del polinomio posso considerarlo come il coefficiente di una lettera elevata a zero. Ad esempio $$ 5 = 5 \cdot 1 = 5 \cdot a^0 $$ Quindi, posso riscrivere il polinomio $$ ab^3 + a^2bc + ab + 5 $$ in questa forma equivalente $$ ab^3 + a^2bc + ab + 5a^0 $$ I due polinomi sono uguali. Pertanto, il numero in questione fa parte di un termine di grado zero.
Osservazioni e note
Alcune osservazioni sui polinomi
- Polinomi uguali
Due o più polinomi sono uguali quando sono composti dagli stessi termini, indipendentemente dall'ordine dei termini.Esempio. Questi due polinomi sono uguali $$ 3ab + 2b + 4bc $$ $$ 2b + 4bc + 3ab $$ perché hanno gli stessi monomi.
- Polinomio nullo
Il polinomio nullo è il numero zero.Dimostrazione. Posso considerare lo zero come il prodotto del coefficiente numerico nullo (zero) per una lettera qualsiasi. Ad esempio $$ 0 = 0 \cdot a $$ Quindi, lo zero è anche un monomio (monomio nullo). La somma di due o più monomi nulli compone un polinomio uguale a zero, ossia un polinomio nullo. Ad esempio $$ 0 \cdot a + 0 \cdot b = 0 $$ In conclusione, il numero zero è sia un monomio nullo che un polinomio nullo.
- Ogni monomio è un polinomio
Posso considerare ogni monomio come la somma di se stesso con il monomio nullo.Ad esempio, questa somma è composta da monomi diversi e forma un polinomio. $$ 3ab + 0 $$ Quindi, ogni monomio è a sua volta un polinomio. $$ 3ab + 0 = 3ab $$
- L'insieme dei polinomi include l'insieme dei monomi e dei numeri reali
L'insieme dei monomi è un sottoinsieme dell'insieme dei polinomi. A sua volta, poiché l'insieme dei numeri reali è un sottoinsieme dei monomi, è anche un sottoinsieme dei polinomi. Pertanto, l'insieme dei polinomi include sia l'insieme dei numeri reali che l'insieme dei monomi.
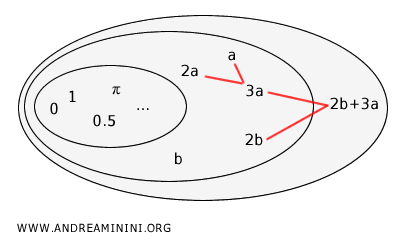
Nota. La somma di monomi non è un’operazione chiusa nell’insieme dei monomi, poiché il risultato può essere un polinomio (ad esempio, \( 2b + 3a \)). Tuttavia, la somma di un monomio con se stesso (es. \( a + a = 2a \)) oppure con lo zero o monomio nullo (es. \( 2a + 0 = 2a \)) restituisce sempre un monomio. Di conseguenza, ogni monomio è anche un polinomio (es. \( 2a = 2a + 0 \): è contemporaneamente un monomio e un polinomio), ma non vale il contrario: non ogni polinomio è anche un monomio (es. \( 2b + 3a \) è un polinomio, ma non è un monomio).
- Polinomio nullo
Il polinomio nullo è lo zero, perché lo zero posso vederlo sia come un monomio nullo $ 0 = 0 \cdot a^0 $ sia come una somma algebrica di monomi nulli $ 0 = 0 \cdot a^0 + 0 \cdot b^0 $. - Polinomio omogeneo
Il polinomio è detto polinomio omogeneo quando tutti i termini del polinomio hanno lo stesso grado (4).Ad esempio, questo polinomio è omogeneo perché tutti i termini sono di grado quattro. $$ ab^3 + a^2bc + b^3a $$
- Polinomio opposto
Il polinomio opposto di P(x) è un polinomio -P(x) con gli stessi termini cambiati di segno.
Ad esempio, se considero questo polinomio $$ P(x): \ a^3 -2 a^2b + bc $$ il polinomio opposto è $$ -P(x): \ -a^3 +2 a^2b - bc $$
- Polinomio ordinato
Il polinomio è detto polinomio ordinato rispetto a una lettera, se i suoi termini sono disposti con gli esponenti della lettera in ordine crescente o decrescente.Ad esempio, questo polinomio è ordinato rispetto alla lettera "a" ma non rispetto alla lettera "b" $$ 3a^4+a^3b + a^2b^3 + 3b $$
- Polinomio completo
Il polinomio è detto polinomio completo rispetto a una lettera, se ha tutte le potenze della lettera in questione dal grado più alto fino allo zero.Ad esempio, questo polinomio è completo rispetto alla lettera "a" $$ a^3b + a^2b^3 + 3ab + 3 $$ Sapendo che il termine noto 3 posso scriverlo come 3=3·1=3a0.
E così via.
