Limite sinistro
Una funzione f(x) definita in un intervallo (a,c) ha il limite sinistro per x che tende a c da sinistra, $$ \lim_{x \rightarrow c^-} f(x) = l $$ se fissato un ε>0 esiste un δ>0 tale che se $$ c-δ<x<c \text{ allora } |f(x)-l|<ε $$
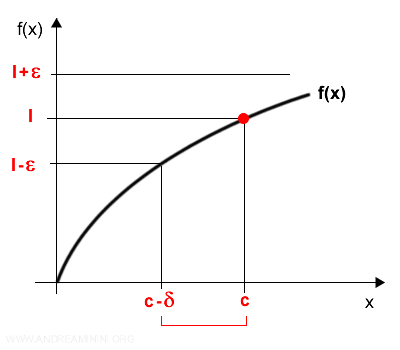
Nel limite sinistro la definizione di limite è soddisfatta nell'intervallo aperto di numeri (c-δ,c) inferiori a c.
Nota. Quando si calcola il limite sinistro di una funzione in un punto c, non si calcola il limite nell'intervallo di numeri superiori di c ( limite destro ), né per il punto c stesso. Potrebbero esistere oppure no.
Un esempio pratico
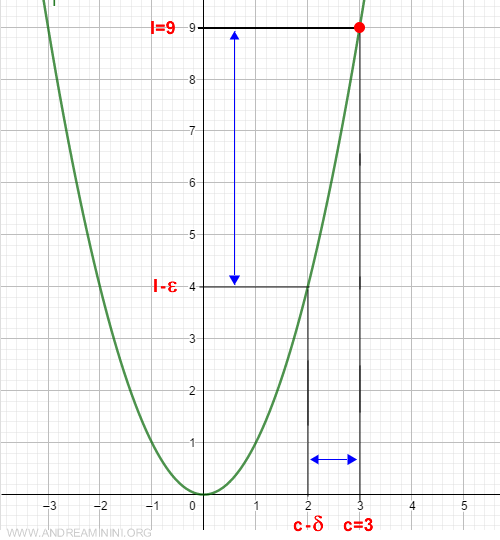
Prendo la funzione f(x)=x2 e il punto c=3
Il limite sinistro della funzione è
$$ \lim_{x \rightarrow 3^-} f(x) = 9 $$
Verifica
Come prima cosa, fisso un valore arbitrario ε=5 maggiore di zero.
$$ l - ε = 9 - 5 = 4 $$
che mi permette di individuare un valore δ=1 maggiore di zero e un intervallo
$$ (c-δ,c) = (3-1, 3) = (2,3 ) $$
Per ogni valore x compreso nell'intervallo aperto (2,3) sull'asse delle ascisse x, la differenza assoluta tra il valore della funzione f(x) e il limite sinistro l è inferiore di ε.
Quindi, il limite sinistro della funzione f(x) nel punto c è 9.