Limite destro
Una funzione f(x) definita in un intervallo (c,d) ha il limite destro per x che tende a c da destra, $$ \lim_{x \rightarrow c^+} f(x) = l $$ se fissato un ε>0 esiste un δ>0 tale che se $$ c<x<c+δ \text{ allora } |f(x)-l|<ε $$
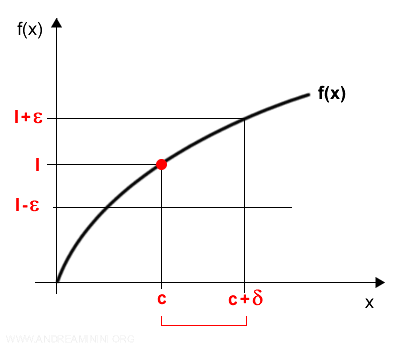
Nel limite destro la definizione di limite è soddisfatta per l'intervallo aperto di numeri (c,c+δ) superiori di c.
Nota. Non viene calcolato il limite per c, né il limite dell'intervallo di numeri inferiori di c. Potrebbero esistere oppure no. Non ha importanza.
Un esempio pratico
Prendo la funzione f(x)=x2 e il punto c=2
Il limite destro della funzione è
$$ \lim_{x \rightarrow 2^+} f(x) = 4 $$
Verifica
Fisso un valore arbitrario ε=5 maggiore di zero.
$$ l + ε = 4 + 5 = 9 $$
che mi permette di individuare un valore δ=1 maggiore di zero e un intervallo
$$ (c,c+δ) = (2, 2+1) = (2,3 ) $$
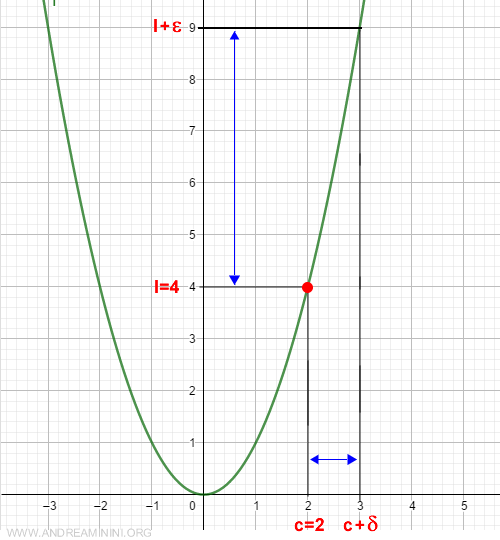
Per ogni valore x compreso nell'intervallo aperto (2,3) sull'asse delle ascisse x, la differenza assoluta tra il valore della funzione f(x) e il limite destro l è inferiore di ε.
Pertanto, il limite destro è 2.
Limite infinito destro per x che tende a x₀
Limite destro +∞
Data una funzione f(x) definita in un intorno destro di $ x_0 $ (ma non necessariamente in $ x_0 $), si dice che f(x) tende a +∞ per x che tende a $ x_0 $ da destra e si scrive: \[ \lim_{x \to x_0^+} f(x) = +\infty \] quando per ogni numero reale positivo $ M>0 $ si può determinare un intorno destro $ I^+(x_0) $ tale che risulti: \[ f(x) > M \] per ogni $ x $ appartenente a $ I^+(x_0) $. \[ \forall \ M > 0 \ \exists \ I^+(x_0) \ | \ f(x) > M,\ \forall \ x \in I^+(x_0) \]
In questo caso si dice anche che la funzione f diverge positivamente a destra di $ x_0 $.
Ad esempio, considero la funzione
\[ f(x) = \frac{1}{x - 1} \]
Studio il limite per $ x $ che tende a 1 da destra.
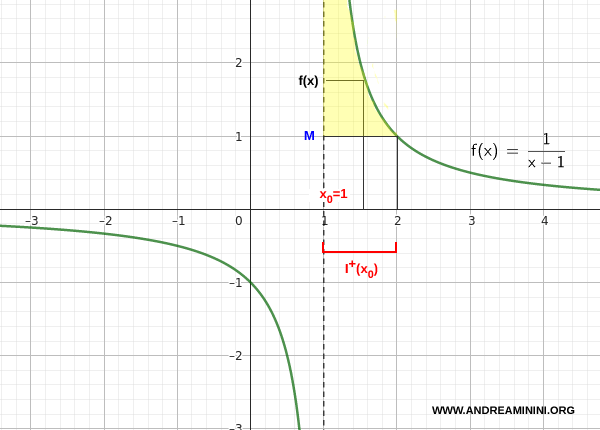
Per $ x > 1 $ il denominatore è positivo e tende a zero. Di conseguenza, f(x) cresce senza limite.
Si ha quindi:
\[ \lim_{x \to 1^+} \frac{1}{x - 1} = +\infty \]
La funzione diverge positivamente a destra di 1.
Limite destro -∞
Si dice che f(x) tende a -∞ per x che tende a x₀ da destra e si scrive: \[ \lim_{x \to x_0^+} f(x) = -\infty \] quando per ogni numero reale positivo $ M > 0 $ si può determinare un intorno destro $ I^+(x_0) $ tale che risulti: \[ f(x) < -M \] per ogni $ x $ appartenente a $ I^+(x₀) 4. \[ \forall \ M > 0 \ \exists \ I^+(x_0) \ | \ f(x) < -M,\ \forall \ x \in I^+(x_0) \]
In questo caso si dice anche che la funzione f diverge negativamente a destra di x₀.
Ad esempio, considero la funzione
\[ f(x) = -\frac{1}{x - 2} \]
Voglio studiare il limite per x che tende a 2 da destra.
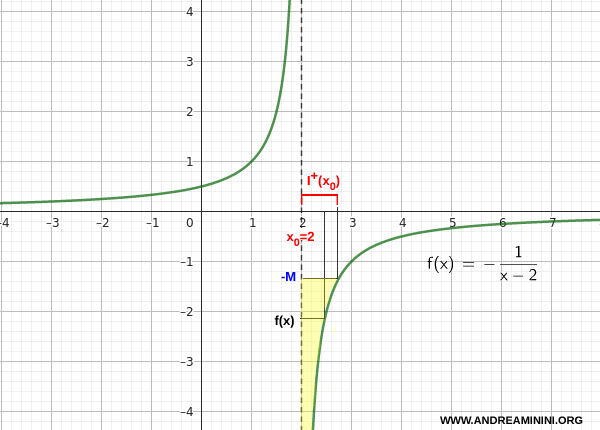
Per $ x>2 $ il denominatore è positivo e tende a zero, ma il segno meno rende il rapporto negativo con valore assoluto sempre più grande.
Si ha quindi:
\[ \lim_{x \to 2^+} \left( -\frac{1}{x - 2} \right) = -\infty \]
La funzione diverge negativamente a destra di 2.
E così via.
