Teorema di Lagrange
Cosa dice il teorema di Lagrange
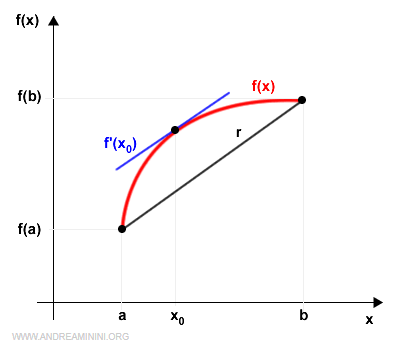
Sia \( f(x) \) una funzione continua nell'intervallo chiuso \( [a,b] \) e derivabile nell'intervallo aperto \( (a,b) \). Allora esiste almeno un punto \(x_0 \in (a,b) \) tale che la derivata della funzione in quel punto è uguale al coefficiente angolare della retta secante passante per i punti \( (a,f(a)) \) e \( (b,f(b)) \):$$ f'(x_0)=\frac{f(b)-f(a)}{b-a} $$
Il teorema di Lagrange è anche detto teorema del valore medio del calcolo differenziale.
Il teorema afferma che esiste almeno un punto dell'intervallo \( (a,b) \) in cui la retta tangente al grafico della funzione è parallela alla retta secante che congiunge i punti \( (a,f(a)) \) e \( (b,f(b)) \).
In altre parole, esiste almeno un punto in cui la tangente ha lo stesso coefficiente angolare della secante.
Il teorema garantisce l'esistenza di almeno un punto con questa proprietà, ma i punti che la soddisfano possono essere anche più di uno.
Nota. La sola continuità non è sufficiente per applicare il teorema di Lagrange. Ad esempio, questa funzione ha i valori estremi \( f(a)=f(b) \) ed è continua in \( [a,b] \) ma non è derivabile nel punto \( x_0 \in (a,b) \). In questo caso non ci sono punti in cui la tangente è parallela alla retta \( AB \).
Un esempio pratico
Ho una funzione f(x)=x2 continua nell'intervallo [0,2] e derivabile in (0,2).
$$ f(x)=x^2 $$
Il punto in cui si verifica il Teorema di Lagrange è
$$ f'(x_0) = \frac{f(b)-f(a)}{b-a} $$
Sapendo che la derivata di f(x)=x2 è f'(x)=2x
$$ 2x_0 = \frac{f(b)-f(a)}{b-a} $$
Sapendo che gli estremi dell'intervallo sono a=0 e b=2
$$ 2x_0 = \frac{f(2)-f(0)}{2-0} $$
$$ 2x_0 = \frac{4-0}{2-0} $$
$$ 2x_0 = 2 $$
Pertanto, il punto x0 è uguale a 1
$$ x_0 = \frac{2}{2} = 1 $$
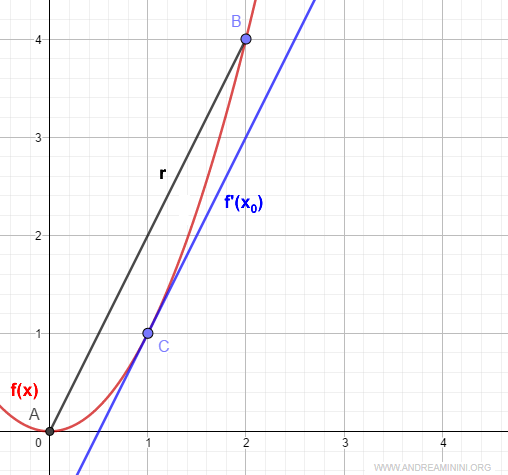
Nel punto x0=1 la derivata f'(x0) è uguale al coefficiente angolare della retta che congiunge gli estremi [a,b].
Dimostrazione e spiegazione
Data una funzione f(x) continua nell'intervallo [a,b] e derivabile nell'intervallo (a,b).
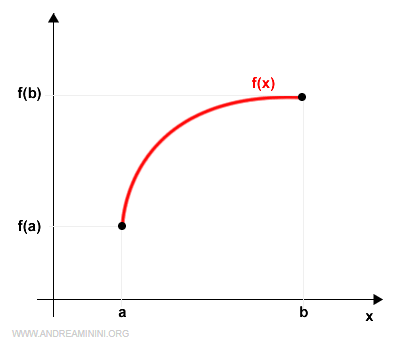
La retta che congiunge i due punti estremi a e b è la seguente:
$$ r: f(a)+\frac{f(b)-f(a)}{b-a} \cdot (x-a) $$
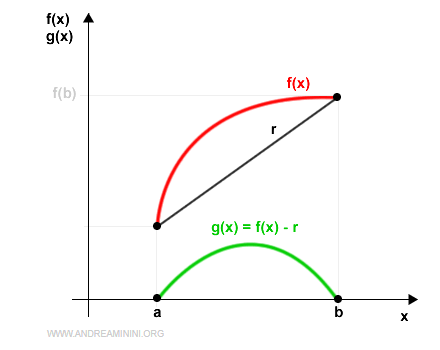
Ecco la rappresentazione grafica sul diagramma cartesiano
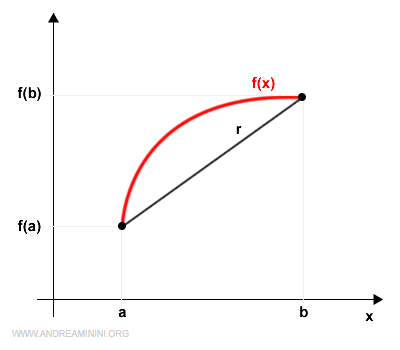
Definisco un'altra funzione g(x) per esprimere la differenza tra f(x) e la retta r.
$$ g(x) = f(x) - r $$
$$ g(x) = f(x) - [ f(a)+\frac{f(b)-f(a)}{b-a} \cdot (x-a) ] $$
La differenza f(x)-r è nulla nei punti estremi a e b.
Quindi anche la funzione g(x) è nulla nei punti a e b.
Verifica. Se x=a la funzione g(x) è nulla. $$ g(x) = f(x) - [ f(a)+\frac{f(b)-f(a)}{b-a} \cdot (x-a) ] $$ $$ g(a) = f(a) - [ f(a)+\frac{f(b)-f(a)}{b-a} \cdot (a-a) ] $$ $$ g(a) = f(a) - [ f(a)+\frac{f(b)-f(a)}{b-a} \cdot 0 ] $$ $$ g(a) = f(a) - [ f(a) ] $$ $$ g(a) = f(a) - f(a) $$ $$ g(a) = 0 $$ Se x=b la funzione g(x) è nulla. $$ g(x) = f(x) - [ f(a)+\frac{f(b)-f(a)}{b-a} \cdot (x-a) ] $$ $$ g(b) = f(b) - [ f(a)+\frac{f(b)-f(a)}{b-a} \cdot (b-a) ] $$ $$ g(b) = f(b) - [ f(a)+ f(b)-f(a) ] $$ $$ g(b) = f(b) - f(b) $$ $$ g(b) = 0 $$
Poiché la funzione g(x) è uguale agli estremi
$$ g(a)=g(b)=0 $$
secondo il teorema di Rolle esiste un punto intermedio x∈(a,b) con derivata nulla g'(x0)=0.
$$ g'(x_0)=0 $$
A questo punto calcolo la derivata prima della funzione g(x) nell'intervallo (a,b)
$$ D[g(x)] = D[f(x) - [ f(a)+\frac{f(b)-f(a)}{b-a} \cdot (x-a) ] ] $$
$$ g'(x) = D[f(x)] - D[ f(a)+\frac{f(b)-f(a)}{b-a} \cdot (x-a) ] $$
$$ g'(x) = f'(x) - \frac{f(b)-f(a)}{b-a} $$
Sapendo che nel punto x0 la derivata g'(x)=0 è nulla
$$ 0 = f'(x) - \frac{f(b)-f(a)}{b-a} $$
con un semplice passaggio algebrico ottengo l'uguaglianza tra la derivata prima e il coefficiente angolare della retta che congiunge gli estremi a e b.
$$ f'(x) = \frac{f(b)-f(a)}{b-a} $$
Dal punto di vista grafico la retta tangente nel punto x0, ossia la derivata prima di f(x) in x0, ha lo stesso coefficiente angolare della retta r.
Ho così dimostrato il teorema di Lagrange.
Verifica geometrica. Analizzo il grafico della funzione della dimostrazione precedente.
Secondo il teorema di Lagrange, la tangente nel punto $ x_0 $ è parallela alla retta $ AB $. Quindi le due rette hanno lo stesso coefficiente angolare
$$ \tan \alpha = f'(x_0) $$
Considero il triangolo $ ABH $, essendo un triangolo rettangolo vale la relazione tra un cateto è l'altro cateto moltiplicato per la tangente dell'angolo opposto
$$ \overline{HB} = \overline{AH} \cdot \tan \alpha $$
Da questa ricavo $ \tan \alpha $
$$ \tan \alpha = \frac{ \overline{HB} }{ \overline{AH} } $$
Sapendo che \( \overline{HB} = f(b)-f(a) \) e \( \overline{AH} = b-a \)
$$ \tan \alpha = \frac{ f(b)-f(a) }{ b-a } $$
Poiché $ \tan \alpha = f'(x_0) $
$$ f'(x_0) = \frac{ f(b)-f(a) }{ b-a } $$
Come volevasi dimostrare.
Dimostrazione alternativa
Considero una funzione continua in \( [a,b] \), derivabile in \( (a,b) \), e con lo stesso valore agli estremi:
\[ F(a)=F(b) \]
Poi costruisco una nuova funzione ausiliaria dove \( k \) è un numero reale qualsiasi:
\[ F(x)=f(x)-kx \]
Poiché \( f(x) \) è continua in \( [a,b] \) e derivabile in \( (a,b) \), anche \( F(x) \) ha le stesse proprietà, perché sto solo sottraendo una funzione lineare \( kx \).
Ora scelgo \( k \) in modo che \( F(a)=F(b) \). Quindi impongo:
\[ F(a)=F(b) \]
Così posso applicare il teorema di Rolle.
Sapendo che \( F(a) = f(a)-ka \) e \( F(b) = f(b)-kb \)
\[ f(a)-ka=f(b)-kb \]
Risolvo questa equazione rispetto a \( k \):
\[ f(a)-f(b)=ka-kb \]
\[ f(a)-f(b)=k(a-b) \]
\[ k=\frac{f(a)-f(b)}{a-b} \]
Moltiplico numeratore e denominatore per \( -1 \) e ottengo:
\[ k=\frac{f(b)-f(a)}{b-a} \]
Quindi la funzione diventa:
\[ F(x)=f(x)-\frac{f(b)-f(a)}{b-a}x \]
A questo punto (F(x)) soddisfa tutte le ipotesi del teorema di Rolle: per ipotesi iniziale è continua in \([a,b] \) e derivabile in \((a,b) \), inoltre ha lo stesso valore agli estremi \( F(a)=F(b) \)
Per il teorema di Rolle, allora, esiste almeno un punto \(c \in (a,b) \) tale che \( F'(c)=0 \).
Ora calcolo la derivata di \( F(x) \):
\[ F'(x)=f'(x)-\frac{f(b)-f(a)}{b-a} \]
Quindi, nel punto \( c \), ho:
\[ F'(c)=f'(c)-\frac{f(b)-f(a)}{b-a} \]
Ma Rolle dice che \( F'(c)=0 \), dunque:
\[ f'(c)-\frac{f(b)-f(a)}{b-a}=0 \]
Porto il secondo termine a destra:
\[ f'(c)=\frac{f(b)-f(a)}{b-a} \]
Questa è la tesi del teorema di Lagrange. Come volevasi dimostrare
Note
Alcune osservazioni e note sul teorema di Lagrange.
- Corollario: le funzioni con derivata nulla sono costanti
Se una funzione f(x) è continua nell'intervallo [a,b] e derivabile nell'intervallo (a,b) e per ogni $ x \in (a,b) $ la derivata è nulla $ f'(x)=0 $, allora la funzione è costante per ogni $ x \in [a,b] $
Dimostrazione. Siano \( x_1,x_2 \in [a,b] \) con \(x_1<x_2 \). Poiché per ipotesi \( f \) è continua in \([a,b] \) e derivabile in \((a,b) \), di conseguenza è anche continua in \([x_1,x_2] \) e derivabile in \((x_1,x_2) \). Per il teorema di Lagrange esiste almeno un punto \(c \in (x_1,x_2) \) tale che \[ f'(c)=\frac{f(x_2)-f(x_1)}{x_2-x_1} \] Per ipotesi \( f'(c)=0 \), quindi \[ \frac{f(x_2)-f(x_1)}{x_2-x_1}=0 \] Poiché \(x_2 \neq x_1 \), segue che \[ f(x_2)-f(x_1)=0 \] e dunque \[ f(x_2)=f(x_1) \] Poiché \( x_1 \) e \( x_2 \) sono due punti arbitrari di \( [a,b] \), risulta \( f(x_1)=f(x_2) \) per ogni coppia di punti dell'intervallo. Pertanto la funzione \(f \) assume lo stesso valore in ogni punto di \([a,b] \) ed è quindi costante. \[ f(x)=k \qquad \forall \ x\in [a,b] \] Come volevasi dimostrare.
- Corollario del teorema di Lagrange: funzioni con la stessa derivata differiscono per una costante
Se f(x) e g(x) sono due funzioni continue nell'intervallo chiuso [a,b] e derivabili nell'intervallo aperto (a,b), tali che $ f'(x)=g'(x) $ per ogni $ x \in (a,b) $, allora differiscono per una costante: $$ f(x)-g(x)=k \qquad \forall \ x \in [a,b] $$
Dimostrazione. Costruisco una funzione ausiliaria $ z(x) $ pari alla differenza tra le due funzioni: $$ z(x)=f(x)-g(x) $$ La funzione $ z(x) $ è continua in $ [a,b] $ e derivabile in $ (a,b) $, perché è differenza di funzioni continue e derivabili. La sua derivata è: $$ z'(x)=f'(x)-g'(x) $$ Poiché per ipotesi $ f'(x)=g'(x) $, ne consegue che: $$ z'(x)=0 \qquad \forall \ x \in (a,b) $$ Per il corollario del teorema di Lagrange, se una funzione è continua in $ [a,b] $, derivabile in $ (a,b) $ e ha derivata nulla in $ (a,b) $, allora è costante in $ [a,b] $. Quindi esiste una costante $ k $ tale che: $$ z(x)=k \qquad \forall \ x \in [a,b] $$ Poiché $ z(x)=f(x)-g(x) $, si ottiene: $$ f(x)-g(x)=k \qquad \forall \ x \in [a,b] $$ Come volevasi dimostrare.
E così via.
