I vettori ( matematica )
Cos'è un vettore
Un vettore è un ente matematico caratterizzato da un'intensità (detta modulo), una direzione e un verso.
In altre parole, un vettore è un segmento a cui viene fissato un verso di percorrenza, ovvero un segmento orientato.
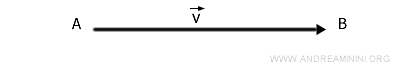
Per indicare che si tratta di un vettore, posso scrivere gli estremi del segmento orientato inserendo una freccia al di sopra (ad esempio $ \overrightarrow{AB} $ ).
In alternativa, posso indicare il vettore con una lettera minuscola, sovrapposta da una freccia (ad esempio $ \vec{v} $ ).
L'origine del vettore è detto punto di applicazione mentre la freccia è detto estremo.

Il segmento indica la direzione mentre la freccia indica il verso del vettore.
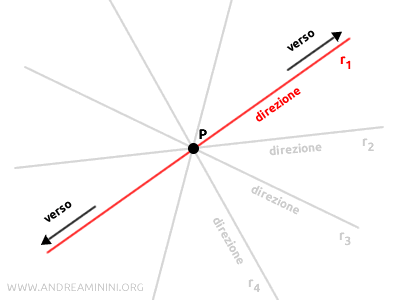
Ad esempio, nel piano, un vettore può assumere infinite direzioni, corrispondenti alle infinite rette che passano per un punto, e ciascuna direzione (retta) può avere due versi opposti.
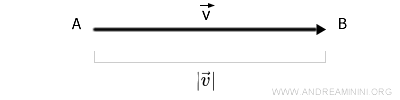
La lunghezza del segmento orientato è detta modulo e si indica ponendo il nome del vettore tra due barre verticali. Ad esempio, $ | \vec{v} | \ \ \text{o} \ \ \ | \overrightarrow{AB} | $
A volte il modulo viene indicato semplicemente con il simbolo del vettore senza la freccia sopra ( ad esempio $ v $ ).
Note. Il simbolo del vettore $ \vec{v} $ non deve essere confuso con il suo modulo $ | \vec{v} | $. Il simbolo $ \vec{v} $ indica tutte le caratteristiche del vettore (direzione, verso, lunghezza) ed è una grandezza vettoriale. Il modulo del vettore $ | \vec{v} | $, invece, indica solo la lunghezza ed è una grandezza scalare (es. un numero reale). Quindi, il modulo $ | \vec{v} | $ è una componente del vettore $ \vec{v} $.
La lunghezza di un vettore rappresenta l'intensità della grandezza fisica o matematica che ho associato al vettore stesso.
In altre parole, essa quantifica "quanto è grande" il vettore, indipendentemente dalla sua direzione.
Ad esempio, in fisica la lunghezza di un vettore forza indica la forza applicata, mentre in matematica rappresenta la distanza dall'origine nello spazio vettoriale.
A cosa servono i vettori?
In fisica alcune grandezze sono caratterizzate dall'intensità, dalla direzione e dal verso.
Ad esempio, lo spostamento nello spazio, la velocità, la forza, l'accelerazione, ecc.
Queste grandezze sono dette grandezze vettoriali e sono rappresentate dai vettori.
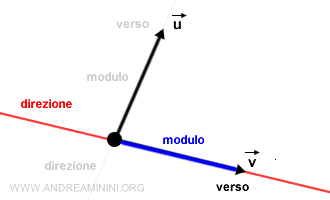
Per rappresentare un vettore disegno un segmento orientato da una freccia.
- La freccia indica il verso del vettore.
- La lunghezza della freccia (modulo o norma) indica l'intensità. E' un numero (scalare).
- La retta in cui si trova la freccia indica la direzione del vettore.
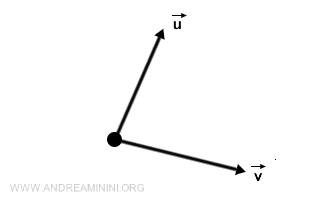
La differenza tra vettore e modulo. Il vettore non va confuso con il suo modulo. E' un errore comune ma grave. Il vettore indica la lunghezza, la direzione e il verso. E' una grandezza vettoriale. Il modulo del vettore, invece, è una grandezza scalare, ossia un numero, che indica soltanto la lunghezza del vettore. Ad esempio, questi due vettori hanno lo stesso modulo (lunghezza) ma sono vettori diversi perché cambia la direzione e il verso.
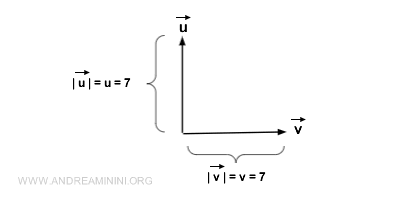
In genere il modulo si indica con lo stesso simbolo del vettore senza freccia o ponendo il simbolo del vettore tra due barre verticali. Il vettore è, invece, indicato con una freccia sopra la lettera oppure con una lettera in grassetto.
Il concetto di vettore in matematica è più ampio ma il concetto resta lo stesso.
Le operazioni tra i vettori
Nei vettori si possono fare due operazioni
- Somma di vettori
Ad esempio, la somma tra due vettori è un terzo vettore
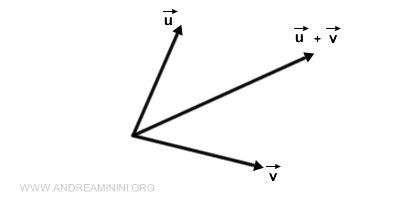
- Prodotto di un numero (scalare) per un vettore
Ad esempio, un vettore moltiplicato per due (scalare) è un vettore con il modulo raddoppiato, stessa direzione e verso.
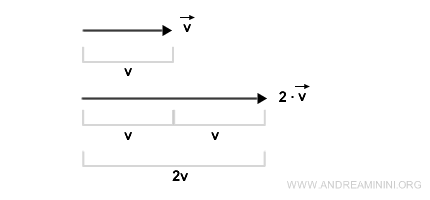
In entrambi i casi il risultato delle operazioni è un altro vettore.
Cos'è un vettore?
Inizio a spiegare i vettori sul piano perché sono i più semplici da capire.
In uno spazio a due dimensioni ( piano x,y ) un vettore è un segmento orientato al quale è assegnato un modulo ( intensità, norma o lunghezza ), una direzione e un verso.
Posso rappresentare un vettore sul piano in questo modo.
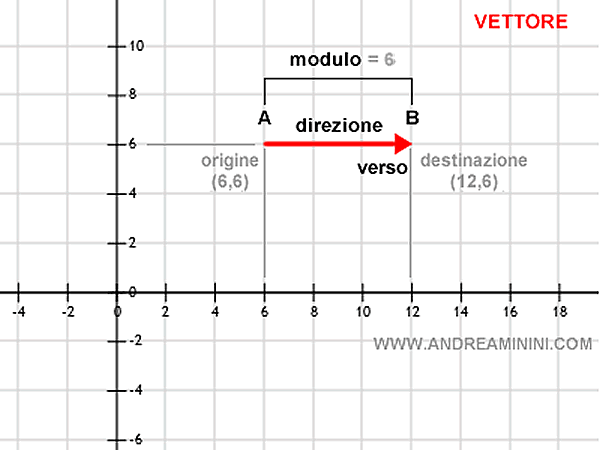
Esempio. In questo piano ho disegnato un segmento di lunghezza 6 ( modulo ) dal punto A (6,6) al punto B ( 12,6 ). Poi ho fissato un verso da A a B. In questo modo ho creato un vettore.
In matematica e in fisica per indicare un vettore si usano le lettere dei punti di origine e di destinazione con una freccia al di sopra
$$ \overrightarrow{AB} $$
oppure semplicemente
$$ AB $$
La differenza tra vettore libero e applicato
Il vettore applicato
Un vettore applicato è un vettore di cui conosco l'origine ( punto di applicazione ).
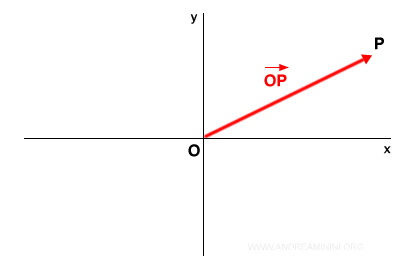
Dato un punto P e il punto O (origine) del piano, il vettore applicato in O con vertice P è la coppia di punti OP. Si indica con una freccia sopra le lettere $$ \overrightarrow{OP} $$ oppure con una lettera minuscola (v, u, w, ecc. )
Ecco un esempio pratico di vettore in O con vertice P sul piano.
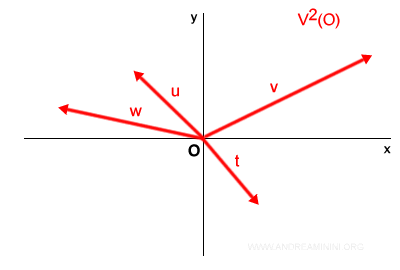
L'insieme di tutti i vettori applicati in un punto di origine O si indica con il simbolo
$$ V^2(O) $$
Ecco un esempio pratico dell'insieme dei vettori applicati nel punto di origine O.
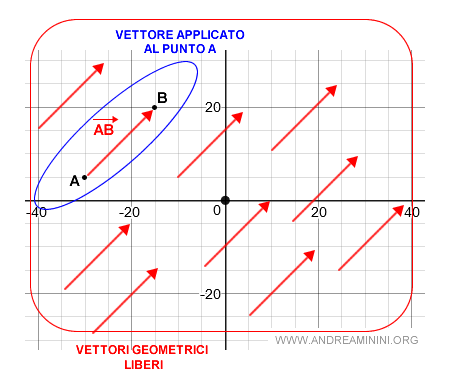
L'origine del vettore può anche essere diversa dall'origine O del piano.
Ad esempio, il segmento orientato AB è un vettore applicato al punto A.
Il vettore libero
In generale un vettore è l'insieme costituito da tutti i segmenti orientati paralleli, con lo stesso verso e la stessa lunghezza (modulo).
Un vettore libero è un vettore di cui non considero l'origine.
L'insieme di tutti i vettori liberi del piano si indica con la lettera V.
$$ V $$
Quando non è specificato il punto di applicazione, si intende il vettore libero ossia l'insieme di tutti i vettori equipollenti.
Nota. In genere, un vettore libero rappresenta l'insieme di tutti i vettori di una classe di equipollenza. E' il rappresentante della classe di equipollenza.
La definizione di vettore in matematica
Un vettore è un elemento di uno spazio vettoriale. Nello spazio vettoriale reale un vettore è una n-pla ordinata di n numeri reali ( x1, ... , xn ).

I numeri reali del vettore sono detti elementi del vettore.
Un esempio pratico
Ecco alcuni esempi di vettori composti da due elementi (n=2) nel campo dei numeri reali.
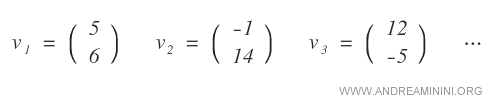
L'insieme di tutti i vettori con due elementi forma lo spazio vettoriale R2 = RxR dei numeri reali.
Lo spazio R2 coincide con tutti i punti del piano cartesiano.
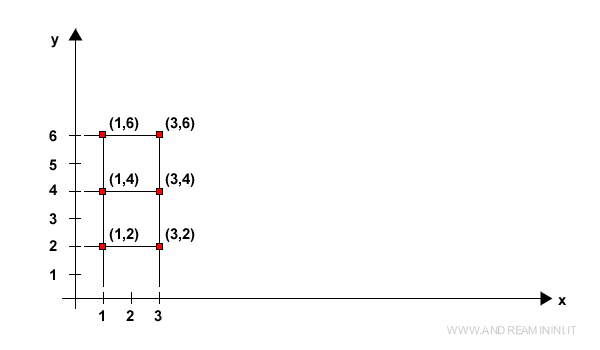
In effetti, ogni coppia di numeri reali ( x1, x2 ) è associata a uno e un solo punto ( x, y ) del piano cartesiano.
La somma dei vettori
Dati due vettori numerici composti da n elementi
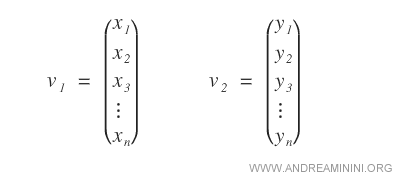
La somma dei vettori è un vettore di n elementi in cui ciascun elemento zn è la somma numerica dei rispettivi elementi xn+yn
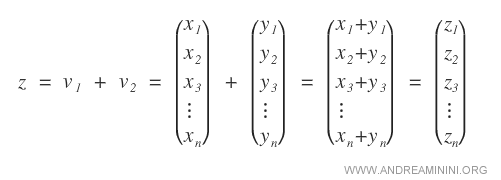
Il prodotto del vettore per uno scalare
Dato un vettore v di n elementi e un numero reale scalare α qualsiasi, il prodotto tra il vettore e lo scalare è un vettore in cui ciascun elemento xn è moltiplicato per lo scalare α.
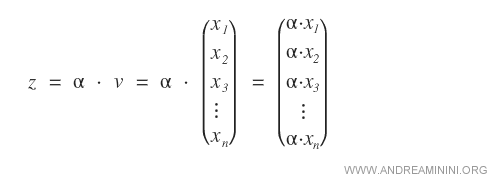
La rappresentazione dei vettori
Nello spazio a due dimensioni i vettori sono rappresentabili sul piano cartesiano.
Due vettori geometrici OE1 e OE2 sono vettori linearmente indipendenti se giacciono su diverse rette passanti per l'origine.
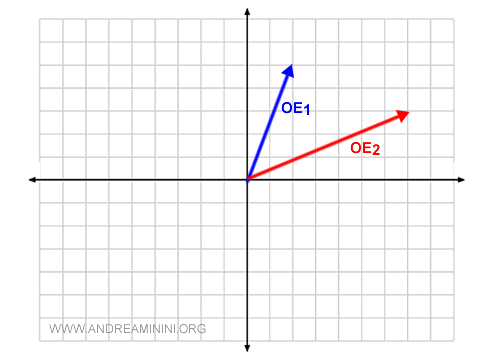
Due vettori indipendenti formano una base dello spazio vettoriale V2O perché la loro combinazione lineare può generare tutti i vettori liberi dello spazio vettoriale a due dimensioni V2.
$$ B = \{ OE_1 , OE_2 \} $$
Ogni punto P del piano è associato a un vettore numerico v(x,y) che identifica le coordinate Cv(x,y) del vettore OP rispetto alla base { OE1, OE2 }.
$$ OP = a_1 \cdot OE1 + a_2 \cdot OE2 $$
D'altra parte vale anche l'inverso, ogni vettore v(x,y) è associato a un punto P del piano tramite la combinazione lineare.
Pertanto, esiste una corrispondenza biunivoca tra i vettori nello spazio R2 e i punti (x;y) del piano.
Un esempio pratico
Utilizzo come base vettoriale B i vettori v1=(0,1) e v2(1,0) ossia OE1 e OE2.
$$ B = \{ v_1 , v_2 \} \\ v_1 = \begin{pmatrix} x \\ y \end{pmatrix} =\begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ v_2 = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$
Oltre a essere linearmente indipendenti, v1 e v2 sono anche perpendicolari tra loro (vettori ortogonali) e facilitano la rappresentazione grafica.
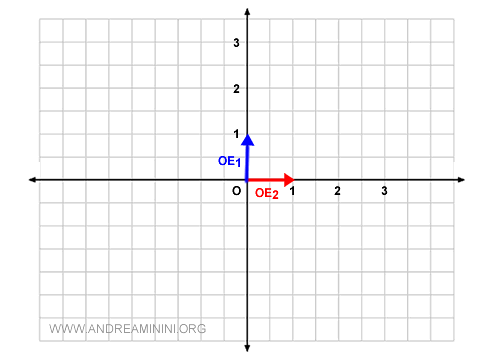
Ora voglio rappresentare il punto P del grafico.
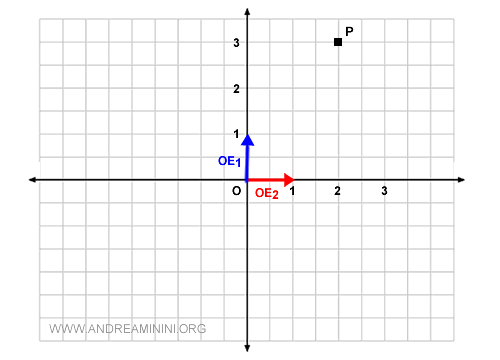
Come ogni punto del piano anche il punto P è associato a un vettore passante per l'origine (O).
In questo caso si tratta del vettore geometrico OP.
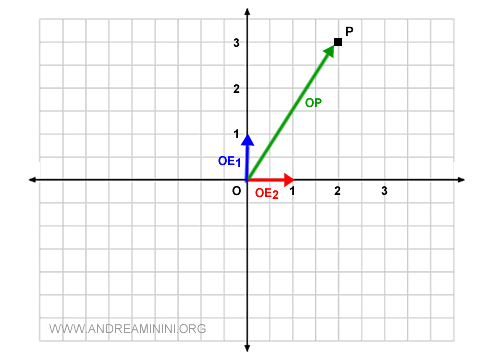
Il vettore OP è lineramente dipendente dai vettori della base { OE1, OE2 } perché può essere rappresentato tramite la loro combinazione lineare.
In pratica, esistono due scalari c1 e c2 detti coordinate tali che:
$$ \overrightarrow{OP} = c_1 OE_1 + c_2OE_2$$
$$ \overrightarrow{OP} = c_1 \begin {pmatrix} 0 \\ 1 \end{pmatrix} + c_2 \begin {pmatrix} 1 \\ 0 \end{pmatrix} $$
$$ \overrightarrow{OP} = 3 \begin {pmatrix} 0 \\ 1 \end{pmatrix} + 2 \begin {pmatrix} 1 \\ 0 \end{pmatrix} $$
$$ \overrightarrow{OP} = \begin {pmatrix} 0 \\ 3 \end{pmatrix} + \begin {pmatrix} 2 \\ 0 \end{pmatrix} $$
$$ \overrightarrow{OP} = \begin {pmatrix} 2 \\ 3 \end{pmatrix} $$
In questo caso la soluzione è molto semplice.
Le coordinate sono c1=3 e c2=2, ossia tre volte il vettore OE1 e due volte il vettore OE2.
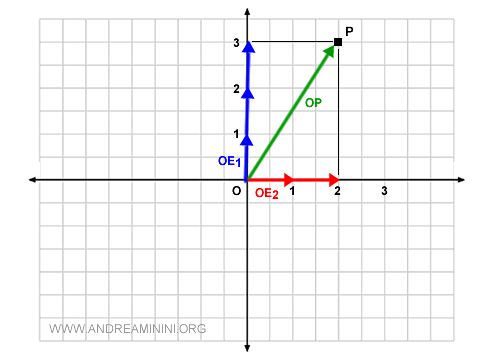
La corrispondenza tra il punto P e il vettore OP è indicata con la seguente relazione di equivalenza:
$$ \overrightarrow{OP} \equiv P \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$
Allo stesso modo posso rappresentare qualsiasi altro punto del piano cartesiano RxR ossia R2.
Nota. La corrispondenza tra punti e vettori è molto utile, perché consente di studiare le proprietà geometriche dei punti e dei vettori tramite l'algebra lineare.
I vettori nello spazio a più dimensioni
Un vettore può essere definito anche nello spazio a più dimensioni.
Vettore nello spazio a due dimensioni
Un vettore nello spazio a due dimensioni (R2) è composto dalla differenza tra i punti di origine e di destinazione del piano.
$$ V \{ x_2-x_1, y_2-y_1 \} $$
Esempio
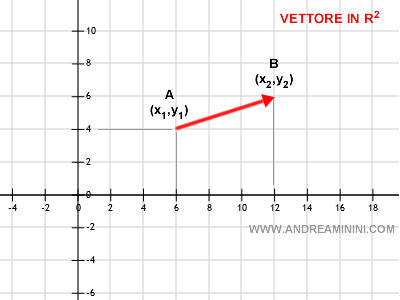
$$ V \{ x_2-x_1, y_2-y_1 \} $$ $$ V \{ 12-6, 6-4 \} $$ $$ V \{ 6, 2 \} $$
Vettore nello spazio a tre dimensioni
In uno spazio a tre dimensioni (R3) la rappresentazione algebrica è simile, ma c'è un'altra coordinata (z) da considerare
$$ V \{ x_2-x_1, y_2-y_1, z_2-z_1 \} $$
Per semplicità negli elementi di un vettore si indica direttamente la differenza ( o accelerazione ).
$$ V \{ x, y, z \} $$
dove
$$ x=x_2-x_1 $$ $$ y=y_2-y_1 $$ $$ z=z_2-z_1 $$
Questa forma è particolarmente utile per studiare i vettori con dimensione superiore.
Un esempio pratico
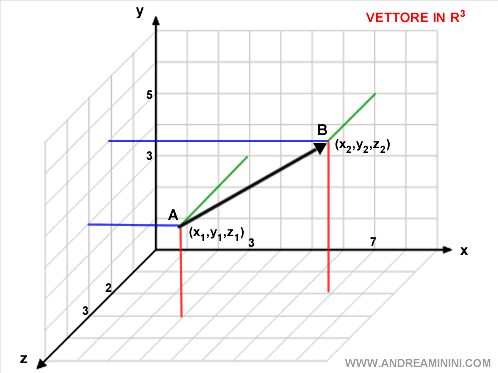
$$ V \{ x_2-x_1, y_2-y_1, z_2-z_1 \} $$ $$ con A=(3,3,3) , B=(7,5,2) $$ $$ V \{ 7-3, 5-3, 2-3 \} $$ $$ V \{ 4, 2, -1 \} $$
Vettore nello spazio a n dimensioni
Il discorso è simile per i vettori negli spazi a n dimensioni (Rn).
$$ V \{ x_1, x_2, x_3, ... , x_n \} $$
In questo caso però qualsiasi rappresentazione geometrica sarebbe incomprensibile per un essere umano.
Perché? Come persone siamo abituati a vedere il mondo in 3 dimensioni. Al massimo possiamo considerare la quarta dimensione come il tempo che scorre. Una quinta o sesta dimensione è difficile da immaginare come forma geometrica. E' un limite dell'uomo. Per rappresentare le realtà più complesse siamo costretti a semplificarle o usare altri metodi di rappresentazione.
Per questa ragione si preferisce rappresentare i vettori a n dimensioni come una n-pla ordinata di n elementi.
$$ V \{ x_1, x_2, x_3, ... , x_n \} $$
Dove gli elementi x1, ... , xn sono numeri reali qualsiasi.
Esempio
$$ V \{ 4, 2, -1, 7 , 3 \} $$
I vettori a più dimensioni sono oggetto di studio dell'algebra lineare.
