Equazione della retta passante per l'origine
L'equazione di una retta passante per l'origine è $$ y=mx $$ dove m è il coefficiente angolare.
Esistono infinite rette passanti per l'origine, ognuna con un coefficiente angolare differente.
$$ m = \frac{y}{x} $$
L'insieme delle retti passanti per l'origine è un fascio proprio di rette.
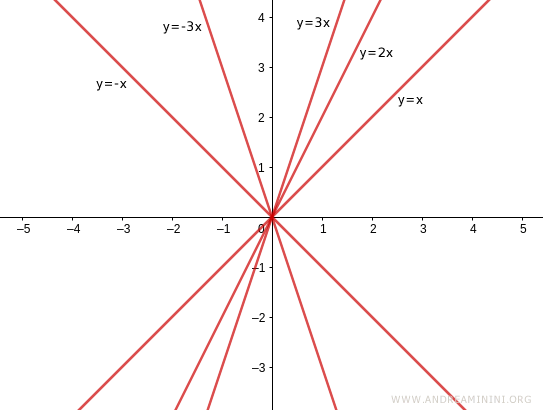
Tuttavia, l'equazione della retta passante per l'origine non esprime tutte le infinite rette. Fa eccezione l'asse verticale.
L'equazione y=mx non può rappresentare l'asse delle ordinate (y) perché non esiste un coefficiente angolare (m) tale da identificare i punti dell'asse verticale.
Esempio. Non è possibile rappresentare il punto (0;1) del piano cartesiano tramite l'equazione y=mx perché la relazione 1=m·0 non può essere soddisfatta in quanto ogni numero moltiplicato per zero è uguale a zero. Lo zero è un elemento assorbente.
E così via.
