Come calcolare il volume del tetraedro con i vettori
Per misurare il volume di un tetraedro, si calcola 1/6 del valore assoluto del determinante della matrice composta da tre vettori del solido. V=16⋅|det(a1a2a3b1b2b3c1c2c3)|
Esempio
Un tetraedro è composto da quattro vertici..
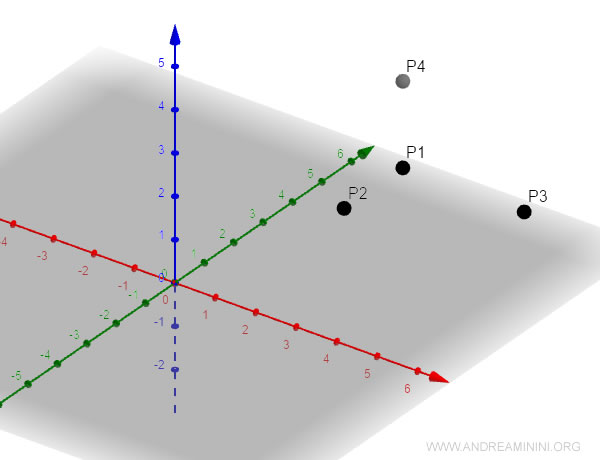
P1(251)P2(231)P3(551)P4(253)
La rappresentazione dei punti nel diagramma cartesiano
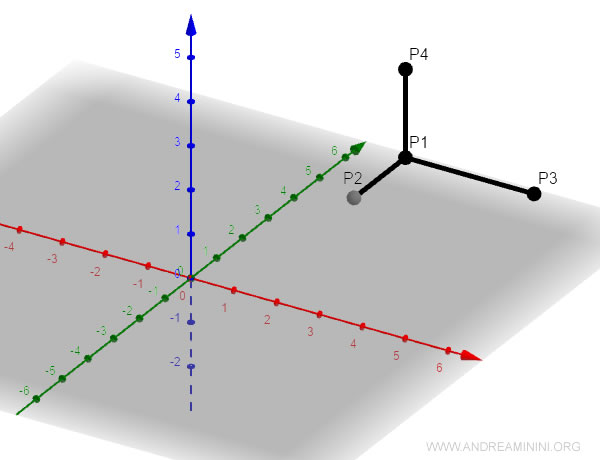
Prendo come riferimento un punto qualsiasi, ad esempio p4, e calcolo tre vettori.
P1P4=(253)−(251)=(2−25−53−1)=(002)
P2P4=(253)−(231)=(2−25−33−1)=(022)
P3P4=(253)−(551)=(2−55−53−1)=(−302)
Questi vettori misurano l'altezza, la larghezza e la profondità del tetraedro.
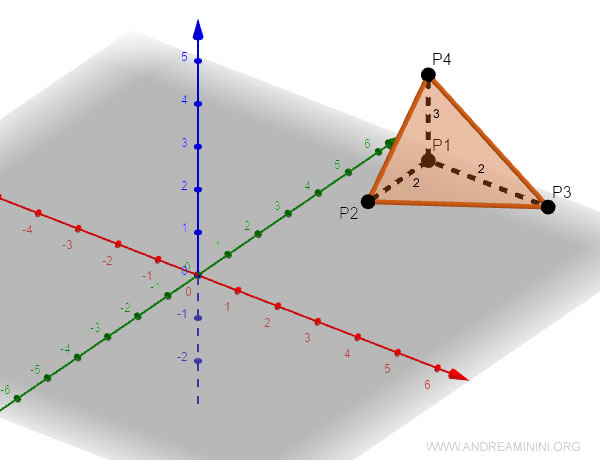
Con i tre vettori compongo una matrice quadrata.
(00−3020222)
Poi calcolo un sesto del valore assoluto del determinante della matrice.
V=16⋅|Δ|=16⋅12=2
Il volume del tetraedro è uguale a 2.
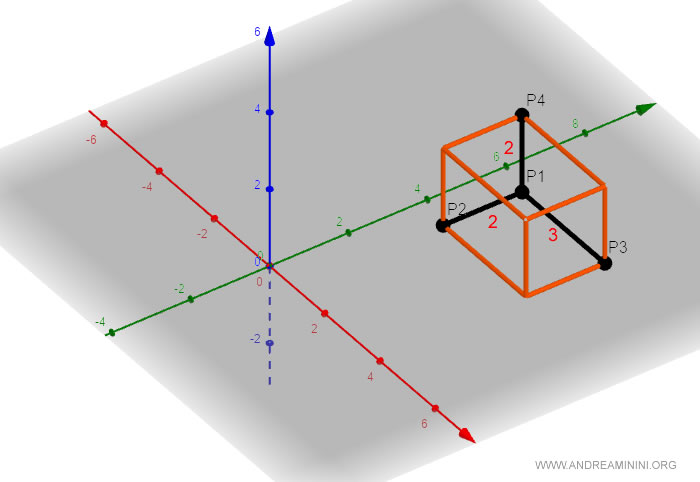
Nota. Il tetraedro è un sesto del volume del parallelepipedo costruito sugli stessi punti.
E così via.


