Come calcolare il volume di un parallelepipedo con i vettori
Il volume di un parallelepipedo può essere misurato nello spazio a tre dimensioni tramite il valore assoluto del determinante dei vettori che lo compongono $$ V = \begin{vmatrix} det \begin{pmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{pmatrix} \end{vmatrix} $$
Esempio
Nello spazio quattro vertici del solido hanno le seguenti coordinate (x,y,z)
$$ P_1 \begin{pmatrix} 2 & 5 & 1 \end{pmatrix} \\ P_2 \begin{pmatrix} 2 & 3 & 1 \end{pmatrix} \\ P_3 \begin{pmatrix} 5 & 5 & 1 \end{pmatrix} \\ P_4 \begin{pmatrix} 2 & 5 & 3 \end{pmatrix} $$
Ecco la rappresentazione nello spazio
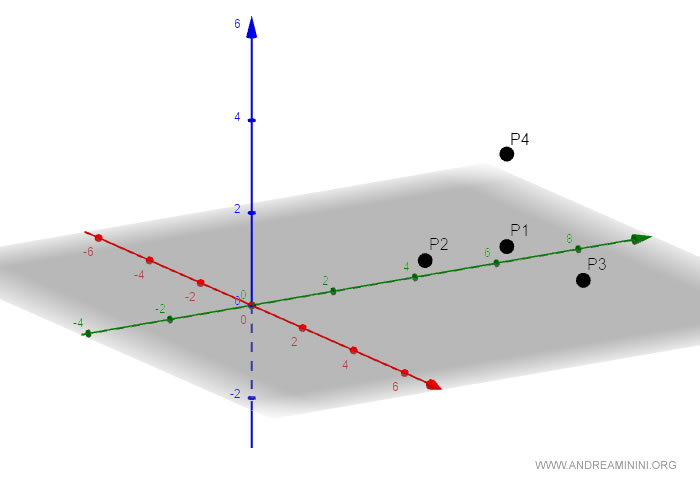
Scelgo un punto qualsiasi come riferimento, ad esempio p4, e calcolo tre vettori.
$$ P_1P_4 = \begin{pmatrix} 2 \\ 5 \\ 3 \end{pmatrix} - \begin{pmatrix} 2 \\ 5 \\ 1 \end{pmatrix} = \begin{pmatrix} 2-2 \\ 5-5 \\ 3-1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 2 \end{pmatrix} $$
$$ P_2P_4 = \begin{pmatrix} 2 \\ 5 \\ 3 \end{pmatrix} - \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} = \begin{pmatrix} 2-2 \\ 5-3 \\ 3-1 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \\ 2 \end{pmatrix} $$
$$ P_3P_4 = \begin{pmatrix} 2 \\ 5 \\ 3 \end{pmatrix} - \begin{pmatrix} 5 \\ 5 \\ 1 \end{pmatrix} = \begin{pmatrix} 2-5 \\ 5-5 \\ 3-1 \end{pmatrix} = \begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix} $$
Sul diagramma cartesiano i vettori misurano rispettivamente l'altezza, la larghezza e la lunghezza del parallelepipedo.
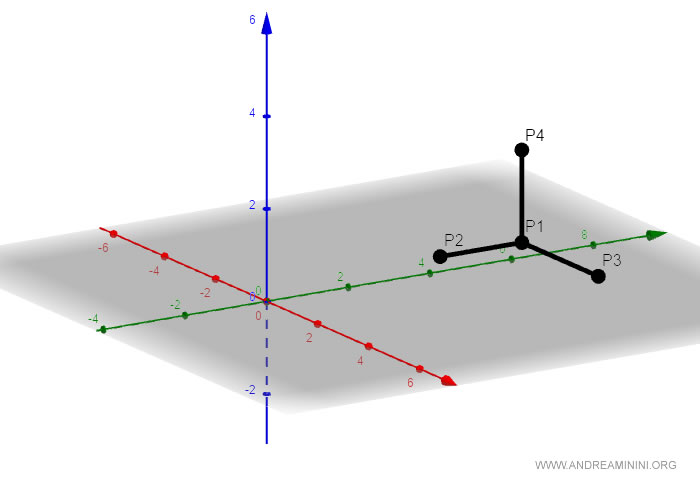
Dispongo i quattro vettori in matrice
$$ \begin{pmatrix} 0 & 0 & -3 \\ 0 & 2 & 0 \\ 2 & 2 & 2 \end{pmatrix} $$
Poi calcolo il determinante della matrice.
$$ Δ = det \begin{pmatrix} 0 & 0 & -3 \\ 0 & 2 & 0 \\ 2 & 2 & 2 \end{pmatrix} =12 $$
Il valore assoluto del determinante Δ è uguale a 12.
$$ | Δ | = 12 $$
Quindi, il volume del parallelepipedo è 12.
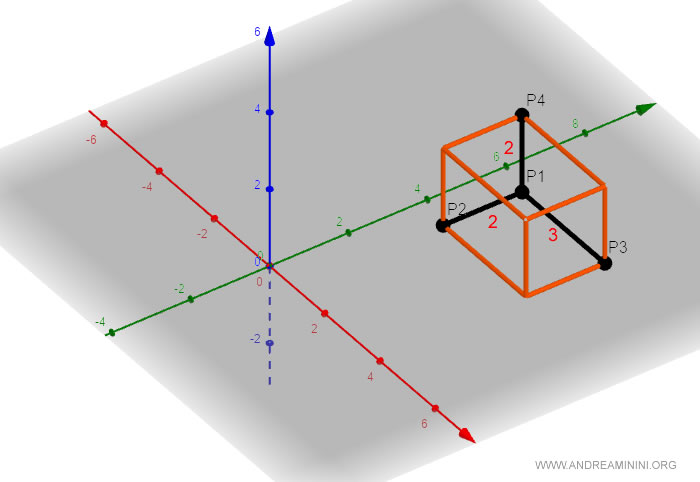
Verifica. La verifica è molto semplice. Il vettore P1P3 è lungo 3 mentre i vettori P1P2 e P1P4 sono entrambi lunghi 2. Il volume di un parallelepipedo è base per altezza per profondità. Quindi, v=3·2·2=12. Il risultato è lo stesso.
E così via.
