Problema di geometria 3

Un trapezio rettangolo ABCD circoscritto a una circonferenza ha gli angoli retti in A e in D e l’angolo acuto in B è di 54°. Sapendo che il perimetro è 5√20, calcola l’area e la lunghezza del lato obliquo BC.

Soluzione

Considero il trapezio rettangolo $ABCD$ con $AB \parallel CD$, avente gli angoli retti in $A$ e $D$.

Posso disporlo nel piano in modo che:

Il punto $A$ sia all'origine $A(0,0)$.
Il lato superiore $AB$ sia orizzontale, quindi $B(a,0)$ per qualche $a>0$.
Poiché l'angolo in $A$ è retto e in $D$ è retto, definisco $D(0,-h)$ in modo che $AD$ sia verticale di lunghezza $h$.
Il lato inferiore $CD$ è parallelo ad $AB$, quindi $C$ avrà coordinate $C(b,-h)$ con $b > a$.

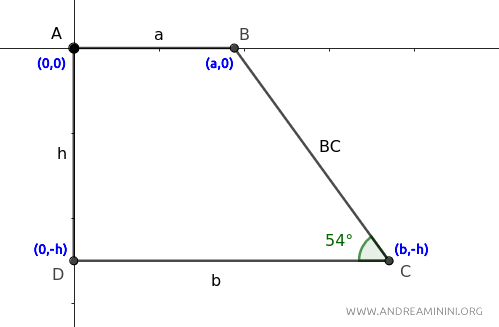
esempio

In sintesi, ho i seguenti punti:

$$ A(0,0), \quad B(a,0), \quad C(b,-h), \quad D(0,-h) $$

Definisco le lunghezze con le seguenti variabili:

$AB = a$
$CD = b$
$AD = h$
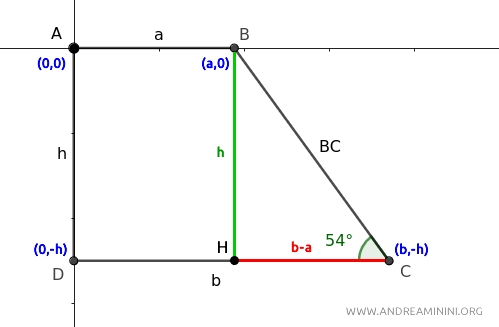
$BC = \sqrt{(b - a)^2 + h^2}$

Il lato $ BC $ l'ho definito usando il teorema di Pitagora sapendo che $ AD = h $ è un cateto e $ CD-AB = b-a $ è l'altro cateto.

esempio

Il perimetro del trapezio rettangolo è dato dal problema $P = 5\sqrt{20}$.

$$ P = AB + BC + CD + DA = 5\sqrt{20} $$

$$ P = a + b + h + BC = 5\sqrt{20} $$

$$ a + b + h + BC = 5 \sqrt{4 \cdot 5} $$

$$ a + b + h + BC = 5 \cdot 2 \sqrt{ 5} $$

$$ a + b + h + BC = 10\sqrt{5} $$

Sapendo che il trapezio è circoscritto ad una circonferenza, il teorema sui quadrilateri circoscritti a una circonferenza afferma che la somma dei lati opposti è uguale.

$$ AB + CD = AD + BC $$

Sostituisco le variabili nell'equazione

$$ a + b = h + BC $$

Quindi, ho due equazioni del problema che posso usare per costruire un sistema:

$$ \begin{cases} a + b = h + BC \\ \\ a + b + h + BC = 10\sqrt{5} \end{cases} $$

Dalla prima equazione ottengo $BC = a + b - h$.

$$ \begin{cases} BC = a + b - h \\ \\ a + b + h + BC = 10\sqrt{5} \end{cases} $$

Sostituisco la prima equazione nella seconda.

$$ \begin{cases} BC = a + b - h \\ \\ a + b + h + (a + b - h) = 10\sqrt{5} \end{cases} $$

Il termine $h$ si cancella:

$$ \begin{cases} BC = a + b - h \\ \\ 2(a + b) = 10\sqrt{5} \end{cases} $$

$$ \begin{cases} BC = a + b - h \\ \\ a + b = \frac{10\sqrt{5}}{2} \end{cases} $$

$$ \begin{cases} BC = a + b - h \\ \\ a + b = 5\sqrt{5} \end{cases} $$

Sostituisco $ a+b $ nella prima equazione con $ 5\sqrt{5} $

$$ \begin{cases} BC = 5\sqrt{5} - h \\ \\ a + b = 5\sqrt{5} \end{cases} $$

A questo punto, devo considerare l'altro dato del problema, ovvero l'angolo acuto in $B$ di $54^\circ$.

Considero il triangolo BCH

esempio

Il cateto orizzontale del triangolo è la differenza delle basi del trapezio $b - a$ mentre il cateto verticale è l'altezza del trapezio rettangolo $h$

Il lato $BC$ scende verso destra formando un angolo di $54^\circ$ con l'orizzontale, dunque:

$$ \tan(54^\circ) = \frac{h}{b - a}. $$

Da questa relazione ottengo che

$$ b - a = \frac{h}{\tan(54^\circ)} $$

A questo punto utilizzo le due relazioni $a+b$ e $b-a$ che ho ottenuto

$$ \begin{cases} a + b = 5\sqrt{5} \\ \\ b - a = \frac{h}{\tan(54^\circ)} \end{cases} $$

Da queste due equazioni, potrei determinare $a$ e $b$ in funzione di $h$, ma poiché non conosco $ h $ devo prima seguire un'altra strada.

Sapendo che $ BC = \sqrt{(b - a)^2 + h^2} $ e anche che $ BC = 5\sqrt{5} - h $ posso scrivere

$$ 5\sqrt{5} - h = \sqrt{(b - a)^2 + h^2} $$

Elevo entrambi i lati al quadrato e semplifico

$$ (5\sqrt{5} - h)^2 = ( \sqrt{(b - a)^2 + h^2} )^2 $$

$$ (5\sqrt{5} - h)^2 = (b - a)^2 + h^2 $$

Sostituisco $b - a = \frac{h}{\tan(54^\circ)}$:

$$ (5\sqrt{5} - h)^2 = \left(\frac{h}{\tan(54^\circ)}\right)^2 + h^2 $$

$$ (5\sqrt{5} - h)^2 = h^2\left(1 + \frac{1}{\tan^2(54^\circ)}\right) $$

Espando il quadrato e semplifico

$$ (5\sqrt{5})^2 - 2 \cdot h \cdot 5\sqrt{5} + h^2 = h^2\left(1 + \frac{1}{\tan^2(54^\circ)}\right) $$

$$ 25 \cdot 5 - 10 \cdot h \sqrt{5} = h^2\left(1 + \frac{1}{\tan^2(54^\circ)}\right) - h^2 $$

$$ 125 - 10 \cdot h \sqrt{5} = h^2\left(1 -1 + \frac{1}{\tan^2(54^\circ)}\right) $$

$$ h^2\left( \frac{1}{\tan^2(54^\circ)}\right) + 10 \cdot h \sqrt{5} - 125 = 0 $$

Sapendo che la tangente di 54° è un valore notevole $ \tan 54° = \frac{ \sqrt{25 + 10 \sqrt{5}} }{5} $

$$ h^2\left( \frac{1}{ ( \frac{ \sqrt{25 + 10 \sqrt{5}} }{5} )^2}\right) + 10 \cdot h \sqrt{5} - 125 = 0 $$

$$ h^2\left( \frac{1}{ \frac{ 25 + 10 \sqrt{5} }{5^2} }\right) + 10 \cdot h \sqrt{5} - 125 = 0 $$

$$ h^2\left( \frac{25}{ 25 + 10 \sqrt{5} }\right) + 10 \cdot h \sqrt{5} - 125 = 0 $$

$$ h^2\left( \frac{5}{ 5 + 2 \sqrt{5} }\right) + 10 \cdot \sqrt{5} h - 125 = 0 $$

Razionalizzo il denominatore

$$ h^2\left( \frac{5}{ 5 + 2 \sqrt{5} \cdot \frac{ 5 - 2 \sqrt{5} }{ 5 - 2 \sqrt{5} } }\right) + 10 \cdot \sqrt{5} h - 125 = 0 $$

$$ h^2\left( \frac{25 - 10 \sqrt{5} }{ 25-20 } \right) + 10 \cdot \sqrt{5} h - 125 = 0 $$

$$ h^2\left( \frac{25 - 10 \sqrt{5} }{ 5 } \right) + 10 \cdot \sqrt{5} h - 125 = 0 $$

$$ h^2\left( 5 - 2 \sqrt{5} \right) + 10 \cdot \sqrt{5} h - 125 = 0 $$

Quest'ultima è un'equazione di secondo grado con $ h $ incognita che si risolve facilmente

$$ h = \frac{ -b \pm \sqrt{b^2-4ac} }{2a} $$

Dove $ a = 5 - 2 \sqrt{5} $, $ b =10 \cdot \sqrt{5} $, $ c = - 125 $

$$ h = \frac{ -10 \cdot \sqrt{5} \pm \sqrt{(10 \cdot \sqrt{5})^2-4 \cdot ( 5 - 2 \sqrt{5} ) \cdot (-125)} }{2 \cdot ( 5 - 2 \sqrt{5} ) } $$

$$ h = \frac{ -10 \cdot \sqrt{5} \pm \sqrt{500 + 500 \cdot ( 5 - 2 \sqrt{5} ) }}{2 \cdot ( 5 - 2 \sqrt{5} ) } $$

$$ h = \frac{ -10 \cdot \sqrt{5} \pm \sqrt{500 (1 + ( 5 - 2 \sqrt{5} ) ) }}{2 \cdot ( 5 - 2 \sqrt{5} ) } $$

$$ h = \frac{ -10 \cdot \sqrt{5} \pm \sqrt{500 (6 - 2 \sqrt{5} ) }}{2 \cdot ( 5 - 2 \sqrt{5} ) } $$

Poiché $ 6 - 2 \sqrt{5} = (1 - \sqrt{5})^2 $

$$ h = \frac{ -10 \cdot \sqrt{5} \pm \sqrt{500 \cdot (1 - \sqrt{5})^2 }}{2 \cdot ( 5 - 2 \sqrt{5} ) } $$

$$ h = \frac{ -10 \cdot \sqrt{5} \pm \sqrt{5 \cdot 10^2 \cdot (1 - \sqrt{5})^2 }}{2 \cdot ( 5 - 2 \sqrt{5} ) } $$

$$ h = \frac{ -10 \cdot \sqrt{5} \pm 10 \sqrt{5} \cdot (1 - \sqrt{5}) }{2 \cdot ( 5 - 2 \sqrt{5} ) } $$

Svolgo i calcoli e giungo alla soluzione $h = 5$.

$$ h = 5 $$

Quindi, sostituisco $ h = 5 $ all'equazione per trovare la lunghezza del lato obliquo BC.

$$ BC = 5\sqrt{5} - h = 5\sqrt{5} - 5 = 5(\sqrt{5}-1) $$

Ho trovato la lunghezza del lato $BC = 5(\sqrt{5} - 1)$.

L'area di un trapezio la ottengo usando la formula:

$$ \text{Area} = \frac{(AB + CD)}{2} \cdot AD = \frac{(a+b)}{2} \cdot h $$

Sapendo che $ a + b = 5\sqrt{5}, \quad h = 5 $ ottengo l'area del trapezio

$$ \text{Area} = \frac{5\sqrt{5}}{2} \times 5 = \frac{25\sqrt{5}}{2} $$

Riepilogando, la lunghezza del lato obliquo $BC$ è

$$ BC = 5(\sqrt{5}-1) $$

L'area del trapezio è:

$$ \text{Area} = \frac{25\sqrt{5}}{2} $$

E così via.