Teorema dei quadrilateri circoscritti
In un quadrilatero circoscritto a una circonferenza, le somme dei lati opposti sono congruenti. $$ \overline{AB}+\overline{CD} \cong \overline{AD} \cong \overline{BC} $$ e viceversa.
Se ho un quadrilatero circoscritto a una circonferenza, i lati del quadrilatero sono tangenti alla circonferenza.
In questo caso la somma di due lati opposti AD+BC è uguale alla somma degli altri due lati opposti AB+CD.
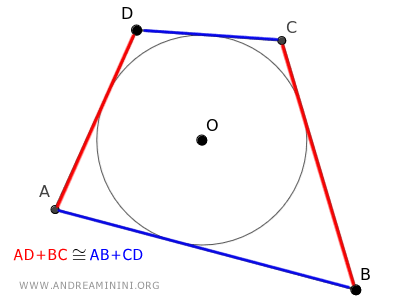
Vale anche il teorema opposto.
Se in un quadrilatero le somme dei lati opposti sono congruenti, allora il quadrilatero è circoscrivibile a una circonferenza.
Pertanto, la congruenza delle somme dei lati opposti è una condizione necessaria e sufficiente affinché il quadrilatero sia circoscrivibile.
La dimostrazione
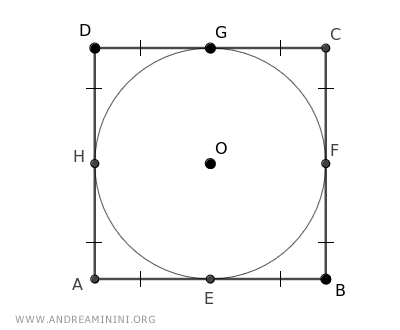
Considero un quadrilatero ABCD circoscritto a una circonferenza con centro O.
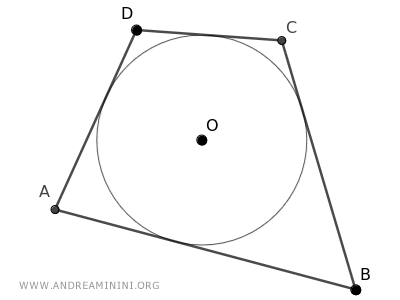
I punti di tangenza del quadrilatero con la circonferenza sono E, F, G, H.
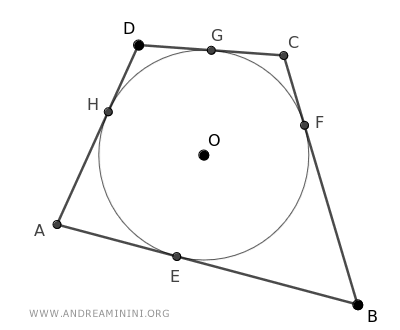
Secondo il teorema delle tangenti di una circonferenza i segmenti AE≅AH sono congruenti, perché il vertice A è un punto esterno alla circonferenza e appartiene a due segmenti tangenti alla circonferenza.
$$ \overline{AE} \cong \overline{AH} $$
Per la stessa ragione sono congruenti anche gli altri segmenti:
$$ \overline{BE} \cong \overline{BF} $$
$$ \overline{CG} \cong \overline{CF} $$
$$ \overline{DG} \cong \overline{DH} $$
Indico le varie congruenze sul quadrilatero.
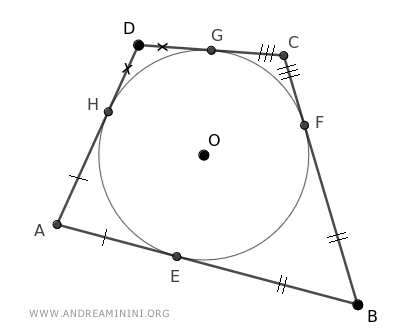
Sapendo che le somme di segmenti congruenti sono a loro volta dei segmenti congruenti, sommo membro a membro tutte le congruenze precedenti.
$$ \overline{AE}+\overline{BE} +\overline{CG} + \overline{DG} \cong \overline{AH} + \overline{BF} + \overline{CF} +\overline{DH} $$
Poi applico la proprietà associativa dell'addizione.
$$ ( \overline{AE}+\overline{BE} ) + ( \overline{CG} + \overline{DG} ) \cong ( \overline{AH} + \overline{DH}) + ( \overline{BF} + +\overline{CF} ) $$
Poiché AB=AE+BE
$$ \overline{AB} + ( \overline{CG} + \overline{DG} ) \cong ( \overline{AH} + \overline{DH}) + ( \overline{BF} + \overline{CF} ) $$
Inoltre, CD=CG+DG
$$ \overline{AB} + \overline{CD} \cong ( \overline{AH} + \overline{DH}) + ( \overline{BF} + \overline{CF} ) $$
Sapendo che AD=AH+DH
$$ \overline{AB} + \overline{CD} \cong \overline{AD} + ( \overline{BF} + \overline{CF} ) $$
Infine, poiché BC=BF+CF
$$ \overline{AB} + \overline{CD} \cong \overline{AD} + \overline{BC} $$
Questo dimostra che le somme dei lati opposti del quadrilatero sono congruenti.

Osservazioni
Alcune osservazioni e note aggiuntive sul teorema
- Il quadrato e il rombo sono due quadrilateri sempre circoscrivibili a una circonferenza
- Nel quadrato i punti di tangenza alla circonferenza coincidono con i punti medi dei lati.
E così via.
