Postulato delle parallele

Il postulato delle parallele o quinto postulato di Euclide afferma che:

Data una retta r e un punto P non appartenente alla retta, esiste una e una sola retta parallela a r che passa per il punto P.

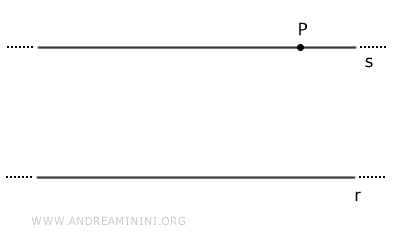
Si tratta di un postulato perché l'unicità della retta parallela non è dedotta da altri teoremi o proprietà della retta. E' una verità accettata come tale.

Viceversa, l'esistenza della retta parallela a r che passa per il punto P può essere dimostrata tramite il teorema delle rette parallele, perché basta trovare una coppia di angoli alterni interni congruenti α≅β.

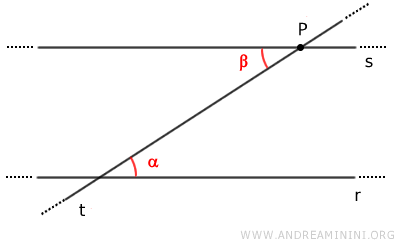
Nota. Questo postulato è noto come quinto postulato di Euclide. Tuttavia, la sua formulazione è successiva a Euclide perché è attribuita a Proclo, un matematico e filosofo bizantino vissuto nel V secolo d.C.

La dimostrazione

Considero una retta r e un punto P del piano che non appartiene alla retta.

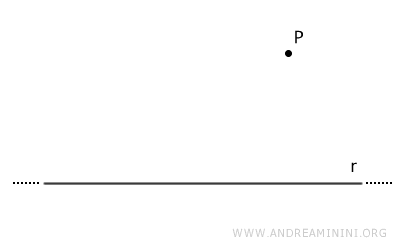
Scelgo in punto P' appartenente alla retta.

Poi traccio una retta t passante per i punti P' e P.

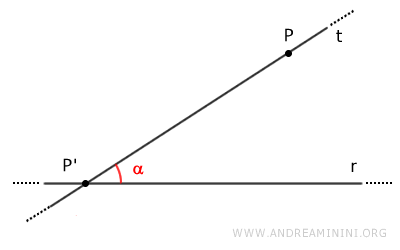
La retta t forma un angolo interno alfa (α) con la retta r.

Traccio un arco con centro P' e raggio PP' che interseca la retta r nel punto A.

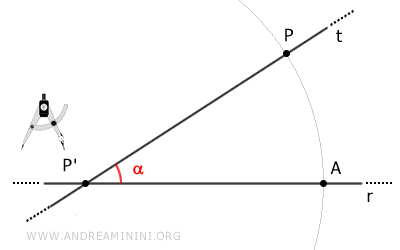
Centro il compasso sul punto P e con la stessa apertura (raggio PP') traccio un secondo arco che passa per il punto P'

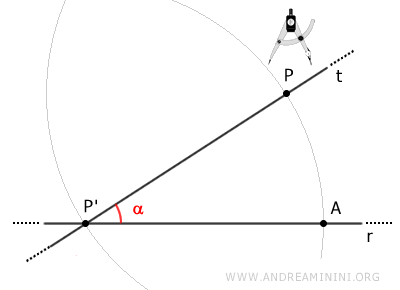
Congiungo i punti A e P con un segmento AP.

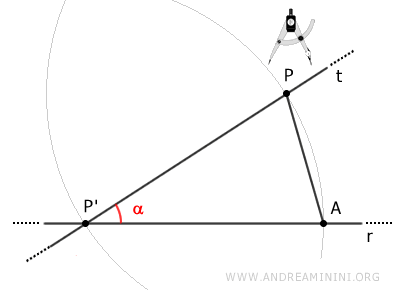
Traccio un terzo arco con centro P' e raggio AP che interseca il secondo arco nel punto B.

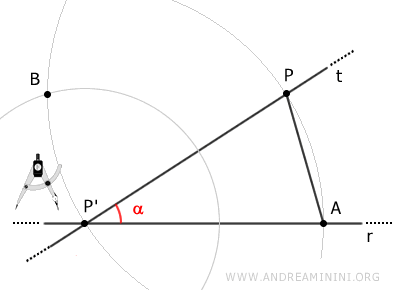
Poi congiungo i punti P' e B con il segmento BP'.

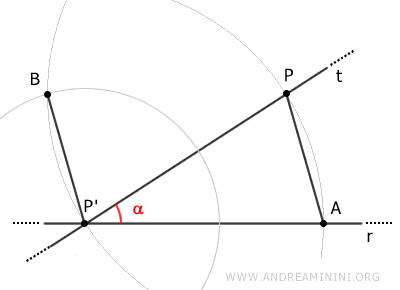
Infine, disegno una retta s passante per i punti B e P.

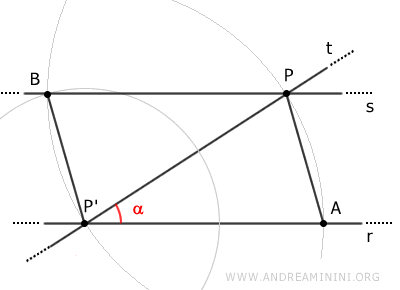
Tra le due rette r e s si formano due triangoli APP' e BPP'

Secondo il terzo criterio di congruenza dei triangoli, i due triangoli APP' e BPP' sono congruenti perché hanno i lati della stessa lunghezza.

$$ APP' \cong BPP' $$

Essendo congruenti, i due triangoli APP' e BPP' hanno gli angoli congruenti nello stesso ordine.

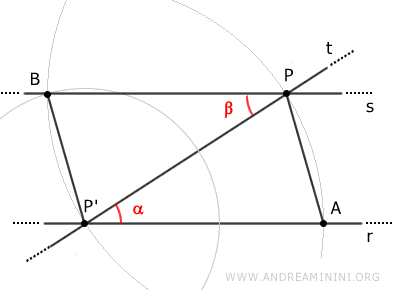
Quindi, l'angolo alfa è congruente all'angolo beta.

$$ \alpha \cong \beta $$

Gli angoli alfa e beta sono angoli alterni interni congruenti (α≅β).

Quindi per il teorema delle rette parallele, le rette r e s sono rette parallele.

In questo modo ho dimostrato l'esistenza della retta s parallela alla retta r che passa per il punto P

Nota. Come già anticipato, l'unicità della retta parallela s non è dimostrabile tramite altre proprietà. Quindi, è considerata come un postulato.

Perché non si può dimostrare l'unicità?

Lo stesso Euclide notò che il cosiddetto quinto postulato sembrava meno evidente e meno “ovvio” degli altri suoi assiomi. Per questo motivo cercò di usarlo il meno possibile e solo quando strettamente necessario.

Per secoli i matematici hanno tentato di dimostrare il quinto postulato a partire dagli altri quattro, ma invano. E' indipendente. Ogni dimostrazione usava, in modo nascosto, ipotesi che erano in realtà equivalenti al quinto postulato stesso.

Nel tentativo di dimostrare che per un punto esterno a una retta passa una sola parallela (unicità), come affermava Euclide e come sembrava 'ovvio', provarono anche a modificare la regola.

Ma invece di ottenere un errore o una contraddizione, scoprirono l'esistenza di un intero universo geometrico coerente e alternativo.

Nota. Girolamo Saccheri provò a fare un ragionamento per assurdo: costruì una geometria ipotetica senza il quinto postulato, sperando che ne emergesse una contraddizione. Invece, non si trovava alcuna contraddizione.

Questo ha portato nel XIX secolo alla nascita delle geometrie non euclidee, in cui il quinto postulato viene sostituito da un’ipotesi diversa:

• Geometria iperbolica (Lobachevskij, Bolyai): In questa geometria per un punto esterno a una retta passano infinite parallele e la somma degli angoli interni di un triangolo è minore di 180°.
  

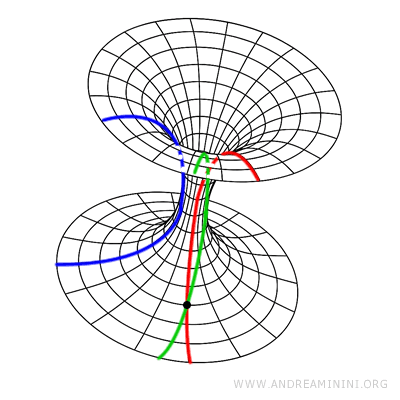
  Nota. Il lavoro di Saccheri, Lobačevskij e Bolyai non bastava da solo a dimostrare che la nuova geometria fosse davvero consistente. Il problema fu risolto da Felix Klein e Henri Poincaré che costruirono dei modelli della geometria iperbolica all'interno della geometria euclidea, dimostrando che la geometria iperbolica era logicamente consistente se è consistente la geometria euclidea. Nel modello di Klein, ad esempio, un "piano" è l’interno di una circonferenza e una "retta" è una corda della circonferenza.

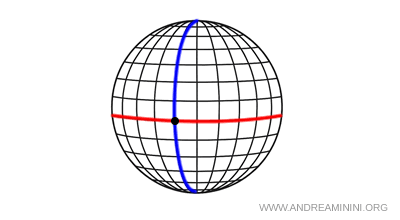
• Geometria ellittica (Riemann): In questa geometria nessuna parallela passa per un punto esterno a una retta. Inoltre,  la somma degli angoli di un triangolo è maggiore di 180°. Ad esempio, in una sfera non esistono rette parallele perché tutte le “rette” sono cerchi massimi e si intersecano sempre.
  

La scoperta delle geometrie non euclidee fu uno dei grandi risultati del ‘800.

Permise di capire che alcune proprietà dipendono dal quinto postulato (e quindi non sono “universali”) e gli assiomi di Euclide non sono gli unici possibili per costruire una geometria coerente.

Nacque anche l’idea moderna di assioma come qualcosa che si assume come vero, non qualcosa che è vero in assoluto.

In generale, l'esistenza delle geometrie non euclidee ha dimostrato che la nozione di spazio non è assoluta, e che lo spazio può essere concepito in modi alternativi e altrettanto validi, con profonde conseguenze per la matematica e la fisica.

In parole povere, con il quinto postulato ci si rende conto che non esiste una sola geometria “vera”, ma tante geometrie possibili, tra le quali la geometria euclidea è solo un caso particolare. Non è però chiaro quale geometria rappresenti meglio la realtà. La relatività di Einstein dice che la gravità curva lo spazio. Vicino ai buchi neri, per esempio, questa curvatura è fortissima. Quindi, per capire la geometria globale dell’universo, dovremmo sapere se è piatto (euclideo) oppure curvo (non euclideo). Attualmente si pensa che, se c’è curvatura, questa è comunque molto piccola e l’universo appare quasi piatto.

E così via.